[C] 재귀를 사용한 하노이의 탑 구현

김태희·2023년 12월 19일

C 자료구조와 알고리즘

C로 배우는 자료구조와 알고리즘 시리즈

목록 보기

23/31

재귀를 사용한 하노이의 탑 구현

최근 군대에서 영어와 경제 공부를 개발 공부와 병행하느라 자료구조 공부 비중이 이전보다 줄었다.

이전보다 포스팅의 주기는 길어질지라도 꾸준히 학습한 내용을 작성할 예정이다.

하노이의 탑(Towers of Hanoi)

하노이의 탑은 A 기둥에 있는 원반을 최소의 횟수로 C 기둥으로 옮기는 문제이다.

이때 원반을 1개씩만 옮겨 작은 원반부터 점차 큰 원반까지 위에서 아래로 순서대로 위치할 수 있도록 해야하고, 큰 원반을 작은 원반 위에 쌓을 수는 없다.

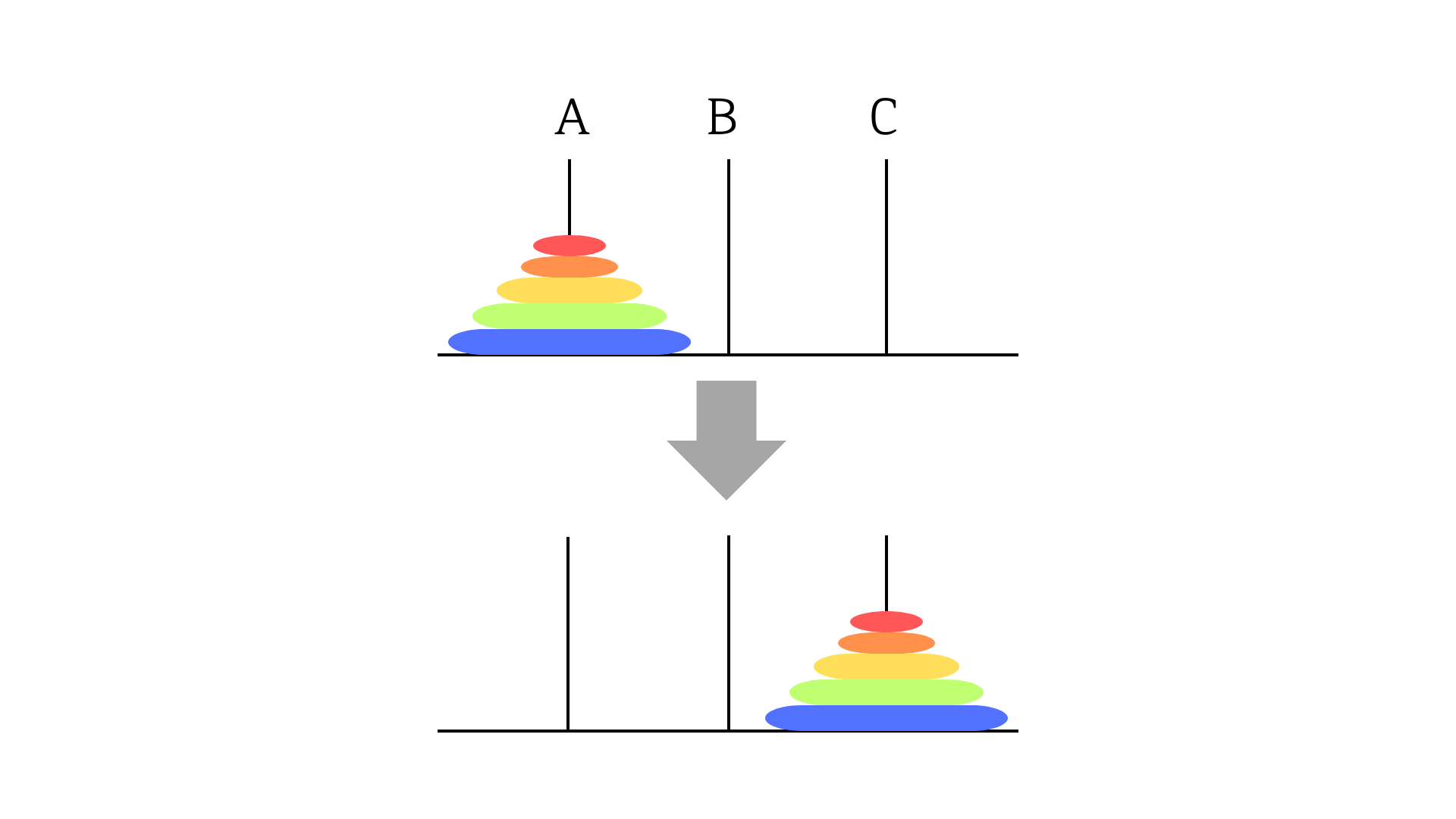
이와 같이 생긴 하노이의 탑을 재귀로 구현하기 전에 해결과정을 일반화 시켜보겠다.

원반이 3개일 때의 과정

1       |       |
2-      |       |
3--     |       |
-------------------
A       B       C

먼저 하노이의 탑을 해결하기 위한 기본은 가장 아래의 원반을 꺼내는 것이다.

그러려면 다른 곳에다 더 작은 원반을 옮겨놓는 방식으로 결국엔 가장 아래에서 한 칸 위의 원반도 꺼내야한다.

|       |       |
2-      |       |
3--     |       1
-------------------

|       |       |
|       |       |
3--     2-      1
-------------------

|       |       |
|       1       |
3--     2-      |
-------------------

|       |       |
|       1       |
|       2-      3--
-------------------

|       |       |
|       |       |
1       2-      3--
-------------------

|       |       |
|       |       2-
1       |       3--
-------------------

|       |       1
|       |       2-
|       |       3--
-------------------

이와 같이 원반이 3개일때 3번 원반을 C로 옮기기 위해 1번과 2번을 B로 옮겨야만 했다.

그 다음엔 (원반이 2개일때의 풀이와 같이) 2번을 꺼내기 위해 1번을 A로 옮겨야만 했다.

이처럼 하노이의 탑에는 반복되는 규칙이 있다.

A의 가장 아래의 원반을 C로 꺼내기 위해서 B에다가 가장 아래의 원반을 제외한 탑을 만든다.

B에 만들어진 탑에서 가장 아래의 원반을 C로 꺼내기 위해서 A에다가 가장 아래의 원반을 제외한 탑을 만든다.

내용이 복잡하니 아래에서 차근차근 다시 살펴보자.

하노이의 탑의 일반화

위의 규칙을 바탕으로 재귀를 구현할 수 있도록 일반화를 해볼 것이다.

n개의 원반을 A에서 C로 이동하기 위한 원반들의 이동

1. n-1개의 원반을 A에서 B로 이동

2. 가장 큰 원반을 A에서 C로 이동

3. n-1개의 원반을 B에서 C으로 이동 (재귀)

마지막 과정에서 출발하는 기둥만 달라졌을 뿐 실제로 위와 같은 과정을 다시 거치면 된다는 사실을 알 수 있다.

이를 바탕으로 코드를 구현해보자.

재귀를 활용한 하노이의 탑 구현

기둥 번호를 1, 2, 3으로 나타내고

원반 n개를 x기둥에서 y기둥으로 옮기는 함수를 만든다고 가정했을때

기둥 번호의 합이 6인점을 이용해 중간 기둥 즉 중간이 아니더라도 목표 기둥과 시작 기둥이 아닌 남는 기둥은 6-x-y를 통해 구했다.

#include <stdio.h>

void move(int n, int x, int y){
  if(n>1) move(n-1, x, 6-x-y); //n을 제외한 기둥을 시작 기둥에서 중간 기둥으로 옮긴다.

  printf("원반[%d] %d 기둥에서 %d 기둥으로 이동\n", n, x, y); //n원반을 마지막 기둥으로 옮긴다.

  if(n>1) move(n-1, 6-x-y, y); //n을 제외했던 기둥을 중간 기둥에서 마지막 기둥으로 옮긴다.
}

void main(){
  int n;
  printf("원반 개수: ");
  scanf("%d", &n);
  move(n, 1, 3);
}

-------------------------------
결과

원반 개수: 3
원반[1] 1 기둥에서 3 기둥으로 이동
원반[2] 1 기둥에서 2 기둥으로 이동
원반[1] 3 기둥에서 2 기둥으로 이동
원반[3] 1 기둥에서 3 기둥으로 이동
원반[1] 2 기둥에서 1 기둥으로 이동
원반[2] 2 기둥에서 3 기둥으로 이동
원반[1] 1 기둥에서 3 기둥으로 이동