[WEEK05] RBTREE - Ⅰ

RBTREE

RBTREE

이진 탐색 트리에서 search, insert, delete의 시간 복잡도는 O(h)이다. 즉, 트리의 높이에 비례한 만큼의 시간이 걸린다. 원소들이 트리에 잘 분산되어 있다면 별 문제가 없으나, 한 쪽으로 치우친 트리(skewd tree)의 경우에는 높이가 n이 되고, 시간 복잡도도 O(n)이 된다.

레드블랙 트리는 이진 탐색 트리의 일종이다. search, insert, delete를 할 때 트리가 한쪽으로 너무 치우치지 않도록 추가적인 작업을 해줌으로써 어느 정도 균형을 맞춰주는 것이다. 그래서 최악의 경우에도 O(logN)을 보장하고 높이또한 O(logN)이 된다.

레드블랙 트리의 기본 구조는 이진 탐색 트리의 기본 구조와 같은데 거기에 추가로 가상의 노드를 만들어야 한다. 자식 노드가 존재하지 않을 때 'NIL'이라는 특수한 노드를 가지게 한다. 그렇기 때문에 모든 리프 노드는 NIL 노드가 된다. 또한 루트 노드의 부모 노드도 NIL 노드로 둔다. 즉, 레드블랙 트리에서 사용되는 노드들은 NIL 노드와 NIL 노드가 아닌 내부 노드로 구분할 수 있다.

RBTREE의 조건

1. 각 노드는 빨간색(RED) 혹은 검은색(BLACK)이다.
2. 루트 노드는 블랙이다.
3. 모든 리프 노드는 블랙이다. 즉, NIL 노드는 모두 블랙이다.
4. 레드 노드의 자식은 모두 블랙이어야 한다. 즉, 레드 노드는 연속적이면 안된다.
5. 모든 노드에 대해 그 노드로부터 자손인 리프 노드에 이르는 모든 경로에는 동일한 개수의 블랙 노드가 존재한다.

h와 bh

h와 bh를 알아야 하는 이유는 search, insert, delete와 같은 연산을 O(logN)안에 할 수 있다는 것을 증명하기 위함이다.

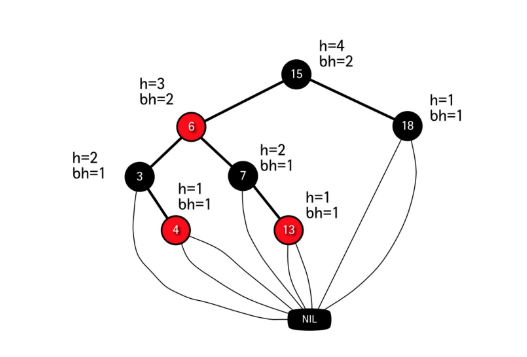
노드 x의 높이 h는 자신으로부터 리프 노드까지의 가장 긴 경로에 포함된 에지의 갯수이다. 예를 들어, 노드 15의 높이는 15-6-7-13으로 이어지는 것이 가장 길기 때문에 4이다.

노드 x의 블랙-높이 bh는 자신으로부터 리프 노드까지의 경로 상에 있는 블랙 노드의 갯수이다. 노드 x 자신은 포함시키지 않는다. 예를 들어, 노드 7의 bh는 7-13-NIL로 이어지므로 자신을 제외한 블랙 노드는 NIL 하나다. 또한 노드 x로부터 왼쪽으로 가든 오른쪽으로 가든 bh는 일정하다. (조건5에 의해)

RBTREE의 높이

• 루트가 x인 노드의 서브트리는 적어도 $2^{bh(x)} - 1$ 개의 내부 노드를 가진다.

위의 bh(x)에 대한 수학적 귀납법으로 증명할 수 있다. bh(x)가 0이면 x는 NIL 노드이므로 이 노드를 루트로 하는 서브 트리는 적어도 $2^{bh(x)} - 1 = 2^0 - 1 = 0$ 개의 내부 노드를 가진다.

귀납적 단계로써, 노드 x가 양의 높이를 가지고 두 자식을 가지는 내부노드라 하면, 각 자식은 자신의 색깔이 레드이냐 또는 블랙이냐에 따라 $bh(x)$ 또는 $bh(x) -1$의 높이를 가진다. 적어도 몇개의 내부 노드를 가지는가를 알아보는 문제이기 때문에 둘다 $bh(x) - 1$의 높이를 가진다고 봐도 문제 없다. 따라서 x를 루트로 하는 서브 트리는 적어도 $(2^{bh(x)-1} - 1) + (2^{bh(x)-1} - 1)$ $+$ $1 =$ $2^{bh(x)} - 1$개의 내부 노드를 가지므로 앞의 명제가 증명되었다.

또한 조건 4에 의해 루트에서 리프로 가는 단순 경로(루트 제외)의 노드 중 절반 이상이 블랙이다. 즉 루트의 $bh(x)$는 적어도 $h/2$이다.

내부 노드의 수를 구할 수 있게 되었으니, 내부 노드의 개수에 따라 높이가 어떻게 결정되는지 알 수 있다. 내부 노드가 n일 때, $n$ $\geq$ $2^{bh(x)} - 1$ $\geq$ $2^{h/2} -1$ 이므로 $n + 1$ $\geq$ $2^{h/2}$로 바꾸고, 양변에 로그를 씌우면 $log(n+1)$ $\geq$ $h/2$, 즉, $2log(n+1)$ $\geq$ $h$이 된다.

$2log(n+1)$ $\geq$ $h$ 이라는 사실에 의해 탐색, 삽입, 삭제와 같은 연산은 레드블랙 트리를 이용하면 $O(logN)$ 시간에 수행할 수 있음을 알 수 있다.

회전

회전은 한 노드를 중심으로 부분적으로 노드의 모양을 수정하는 것이다. 회전을 하더라도 이진 탐색 트리의 특성을 유지한다는 점이 중요하다(레드블랙 트리는 회전하면 레드블랙 트리의 특성을 잃을 수 있다.) 회전에서의 시간 복잡도는 $O(1)$이다.

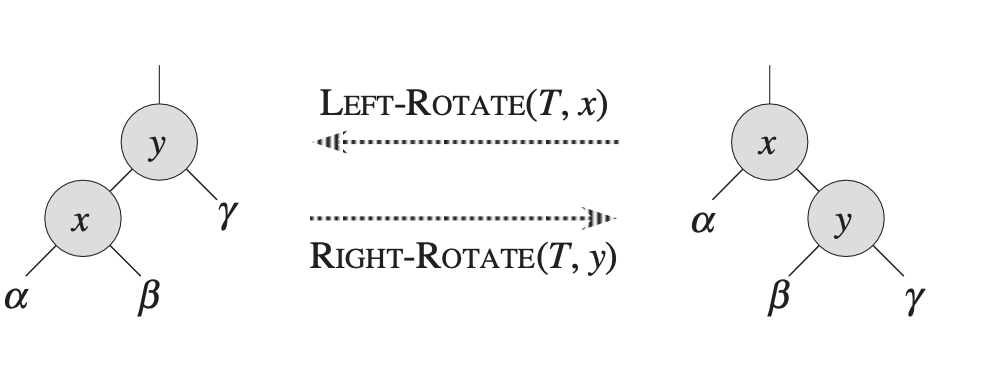
LEFT-ROTATE는 y를 x의 자리로 옮기고, x를 y의 왼쪽 노드로 옮긴다. Right-Rotate는 x를 y의 자리로 옮기고, y를 x의 오른쪽 노드로 옮긴다.

LETE-ROTATE(T, x)

1 y ← right[x]
2 right[x] ← left[y]
3 if left[y] != nil[T]
4 	then p[left[y]] = x
5 p[y] ← p[x]
6 if p[x] == nil[T]
7 	then root[T] ← y
8 	else if x == left[p[x]]
9		then left[p[x]] ← y
10		else right[p[x]] ← y
11 p[x] ← y
12 left[y] = x

RIGHT-ROTATE(T, x)

1 y ← left[x]
2 left[x] ← right[y]
3 if right[y] != nil[T]
4 	then p[right[y]] = x
5 p[y] ← p[x]
6 if p[x] == nil[T]
7 	then root[T] ← y
8 	else if x == left[p[x]]
9		then left[p[x]] ← y
10		else right[p[x]] ← y
11 p[x] ← y
12 right[y] = x

RBTREE 구현 Github 링크
RBTREE