RBTREE
INSERT
RB-INSERT(T, z)
1 x = root[T]
2 y = nil[T]
3 while x != nil[T]
4 do y ← x
5 if key[z] < key[x]
6 then x ← left[x]
7 else x ← right[x]
8 p[z] ← y
9 if y == nil[T]
10 then root[T] ← z
11 else if key[z] < key[y]
12 then left[y] ← z
13 else right[y] ← z
14 left[z] ← nil[T]
15 right[z] ← nil[T]
16 color[z] ← RBTREE_RED
17 RBTREE-INSERT-FIXUP(T, z)레드블랙 트리에서의 삽입은 이진탐색 트리의 삽입과 거의 동일하다.
- line 1~15) 이진탐색 트리에 삽입할 때의 과정과 동일하다.
- line 16) 새로 삽입되는 노드는 빨간색이다.
- line 17) 삽입 후에 레드 노드가 연속해서 등장한 경우에는 red-red violation(레드-레드 위반)이 발생하므로 이것을 고쳐주기 위해 RBTREE-INSERT-FIXUP으로 조정한다.
- z가 루트 노드에 삽입될 경우에도 조건 2인 '루트 노드는 블랙이어야 한다'가 위반된다. 하지만 이 경우에는 삽입 후 루트 노드를 블랙으로 바꿔주면 되므로 큰 문제가 없다.
INSERT FIXUP
RBTREE-INSERT-FIXUP 함수는 6가지 case로 나뉜다.
case 1, 2, 3 은 삽입되는 z의 부모 노드가 할아버지 노드의 왼쪽에 있다.
case 4, 5, 6 은 삽입되는 z의 부모 노드가 할아버지 노드의 오른쪽에 있다.
case 1, 2, 3 과 case 4, 5, 6 은 서로 대칭된다. 그러므로 3가지 경우만 알아본다.
INSERT FIXUP case 1
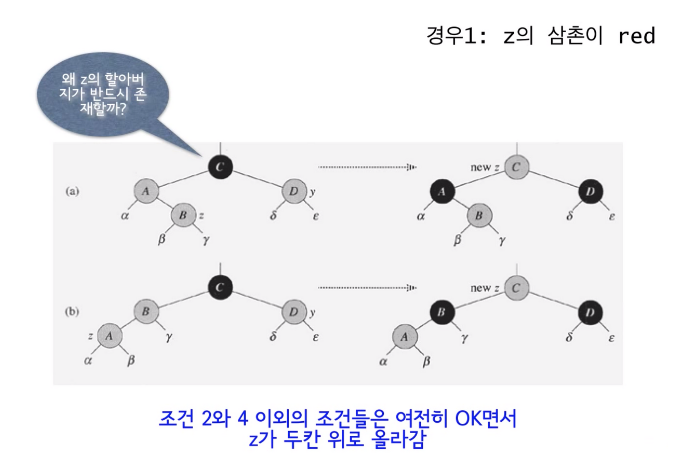
case 1은 z와 z의 부모 노드가 레드이고, 삼촌 노드도 레드인 경우를 말한다.(삼촌 노드란 부모 노드의 형제 노드) 이 경우에는 부모와 삼촌을 블랙으로 바꾸고, 할아버지 노드를 레드 노드로 바꾼다. 이렇게 하면 트리의 구조 자체를 바꾼 것은 아니므로 이진 탐색 트리의 조건을 무너뜨리진 않는다.
- 조건 4를 만족하는가 ?
A, B, D 노드가 그들의 서브트리와 맺는 관계는 아무 문제가 없다. 삽입되는 노드와 부모 노드, 삼촌 노드는 레드이므로 조건 4에 의해 그 자식 노드는 반드시 블랙 노드이기 때문이다.
하지만 할아버지 노드는 블랙이었다가 레드로 바뀌었으므로 할아버지의 아버지 노드와의 관계에서 red-red violation이 발생할 수 있다. 이 경우에는 할아버지 노드를 z로 설정해 다시 case 1을 반복한다. 이 때 red-red violation이 두 레벨 올라간다. 즉, 무한이 반복되는 일은 없으며, 반복되는 횟수는 트리의 높이보다 많을 수 없다.
- 조건 5를 만족하는가 ?
case 1의 경우에는 RBTREE-INSERT-FIXUP을 실행하더라도 경로 상 블랙 노드의 수가 변함없다.
- ps) 왜 z의 할아버지가 반드시 존재할까 ?
부모 노드가 레드인데, 레드 노드는 루트 노드가 될 수 없으므로 블랙인 할아버지 노드가 반드시 존재한다.
INSERT FIXUP case 2, 3
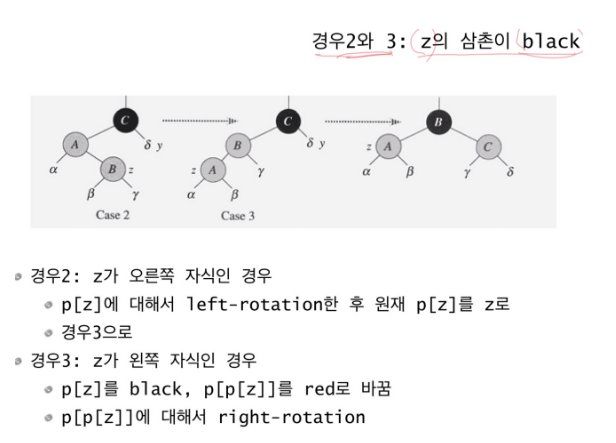
case 2, 3은 삼촌이 블랙인 경우이다.
case 2은 삽입되는 z 노드가 부모 노드의 오른쪽 자식이고, case 3은 부모 노드의 왼쪽 자식이다. case 2은 z의 부모 노드에 대해 left-rotate을 해서 case 3으로 만든다. 이 과정에서 z 노드는 A 노드로 바뀐다.
case 3 에서는 아버지 노드를 블랙 노드로, 할아버지 노드를 레드로 만든 후, 할아버지 노드를 중심으로 right-rotation을 하면 된다.
즉 삽입을 했을 때, case 2라면 left-rotation을 하여 case 3으로 바꿔 right-rotation을 하면 된다. 즉, 두 번의 연산으로 끝난다. 처음부터 case 3이였다면, right-rotation 한 번으로 끝난다. 마지막으로 case 1은 실행 결과에 따라 case 1이 반복적으로 실행될 수도 있고, case 2, 3, 4, 5, 6이 될 수도 있다.
- 조건 4를 위반하는가 ?
알파, 베타, 감마의 경우에는 right-rotation 전이나 후나 부모가 레드 노드이기 때문에 블랙 노드다. 또한 델타의 경우 case 3의 조건이 z의 삼촌이 블랙 노드인 경우이므로 블랙이다. 또한 새롭게 루트가 된 B 노드도 블랙 노드이기 때문에 부모 노드와 red-red violation을 발생시키지 않는다.
- 조건 5를 위반하는가 ?
블랙 노드는 z의 부모 노드 뿐이므로 조건을 만족한다.
INSERT FIXUP pseudo code
RBTREE-INSERT-FIXUP(T, z)
1 while color[p[z]] == RBTREE_RED
// 경우 1, 2, 3
2 do if p[z] == left[p[p[z]]]
3 then y ← right[p[p[z]]]
// 경우 1
4 if color[y] == RBTREE_RED
5 then color[p[z]] ← RBTREE_BLACK
6 color[y] ← RBTREE_BLACK
7 color[p[p[z]]] ← RBTREE_RED
8 z ← p[p[z]]
9 else
// 경우 2
10 if z == right[p[z]]
11 then z ← p[z]
12 LEFT-ROTATE(T, z)
// 경우 3
13 color[p[z]] ← RBTREE_BLACK
14 color[p[p[z]]] ← RBTREE_RED
15 RIGHT-ROTATE(T, p[p[z]])
// 경우 4, 5, 6
16 else (same as then clause with "right"
and "left" exchanged)
17 color[root[T]] ← RBTREE_BLACK레드블랙 트리 T에 z 노드를 삽입하는 수도 코드다.
- line 1) z의 부모 노드가 레드인 경우에, 즉 red-red violation인 동안 while문을 반복한다.
- line 2) z의 부모의 부모, 즉 할아버지 노드의 왼쪽에 z의 부모 노드가 있다는 것으로 위에서 본 case 1, 2, 3이 여기에 해당 된다.
- line 8) 할아버지 노드를 z 노드로 삼아 case 1을 반복한다.
- line 16) z의 부모의 부모, 즉 할아버지 노드의 오른쪽에 z의 부모 노드가 있다는 것이다. 즉 case 4, 5, 6
- line 17) while 문을 빠져나와 line 17로 나오는 경우는 case 3, case 6을 마친 상태이다. 이 때 루트 노드가 레드일 수 있으므로 블랙으로 바꿔준다.
INSERT 시간복잡도
case 2, 3, 5, 6의 경우는 이 걸리고, case 1, 4의 경우 이 걸리므로, 삽입 알고리즘의 시간 복잡도는 이 된다.
RBTREE 구현 Github 링크
RBTREE
