RBTREE
DELETE
TREE-SUCCESSOR(T, x)
1 node ← right[x]
2 while left[node] != nil[T]
3 do node ← left[node]
4 return node
RB-DELETE(T, z)
1 if left[z] == nil[T] or right[z] == nil[T]
2 then y ← z
3 else y ← TREE-SUCCESSOR(t, z)
4 if left[y] != nil[T]
5 then x ← left[y]
6 else x ← right[y]
7 p[x] ← p[y]
8 if p[y] == nil[T]
9 then root[T] ← x
10 else if y == left[p[y]]
11 then left[p[y]] ← x
12 else right[p[y]] ← x
13 if y != z
14 then key[z] ← key[y]
15 copy y's satellite data into z
16 if color[y] == RBTREE_BLACK
17 then RBTREE-DELETE-FIXUP(T, x)
18 free(y)이진탐색 트리의 삭제와 거의 유사하다.
- line 1~15) 이진탐색 트리의 코드를 그대로 옮겨온 것이다.
삭제 이후 다음과 같은 문제가 생길 수 있다.
- 조건 2 위반) 지운 노드가 루트 노드인데 x가 레드 노드일 때
- 조건 4 위반) y 노드의 부모가 레드 노드이고 x 노드도 레드일 경우에 red-red violation이 발생할 수 있다.
- 조건 5 위반) 가장 심각하고 해결하기 어려운 문제이다. 여러 경로 중 한 경로의 블랙 노드만 하나 삭제되므로 조건 5가 위반될 수 있다. 이것을 해결하는 것이 DELETE의 핵심이다.
조건 2, 4의 경우에는 x 노드를 블랙 노드로 바꾸면 해결된다.
조건 5를 해결하기 위해서 RB-DELETE-FIXUP을 하는 것이고, 본격적으로 들어가기 전에 다음과 같은 사전 작업을 해준다. 노드 x 에 "extra black"을 부여해 일단 조건 5를 만족하게 한다. 이 경우 노드 x는 (블랙, 블랙)이 된다. 이 경우 bh(x)는 적어도 2이기 때문에 x의 형제 노드는 NIL일 수 없다.
DELETE FIXUP
RB-DELETE-FIXUP은 8가지 case로 나눌 수 있다.
case 1, 2, 3, 4는 x 노드가 부모 노드의 왼쪽에 있다.
case 5, 6, 7, 8은 부모 노드의 오른쪽에 있다.
case 1, 2, 3, 4 과 case 5, 6, 7, 8 은 서로 대칭된다. 그러므로 4가지 경우만 알아본다.
DELETE FIXUP case 1
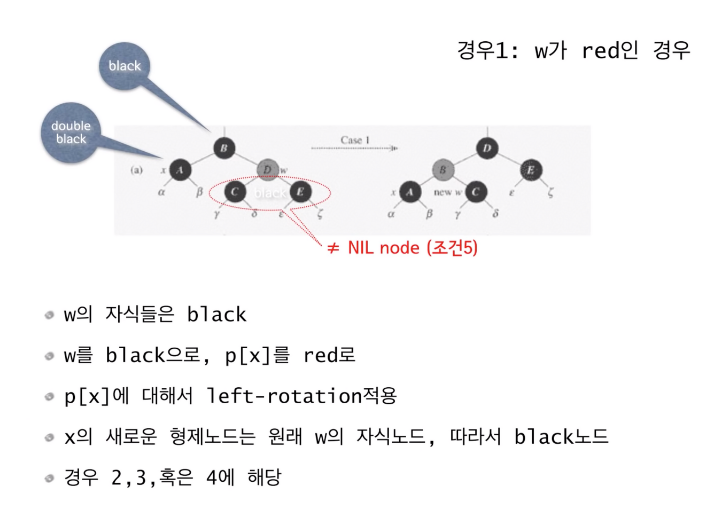
노드 x 의 형제 노드인 w가 레드 노드인 경우다. 이 때 w의 자식인 C와 E는 NIL일 수 없다. NIL이라면 bh(B)가 왼쪽 경로로 가면 2가 나오고, 오른쪽으로 나오면 0이기 때문이다.
w를 블랙 노드로, x의 부모 노드를 레드 노드로 바꾼 후 x의 부모 노드를 기준으로 left-rotation한다.(x 노드가 한 레벨 내려간다) 결과인 오른쪽 그림을 보면 C 노드가 x 의 새로운 형제가 된 것을 확인할 수 있다. 이렇게 됐다면 case 2, 3, 4에 해당된다.
DELETE FIXUP case 2
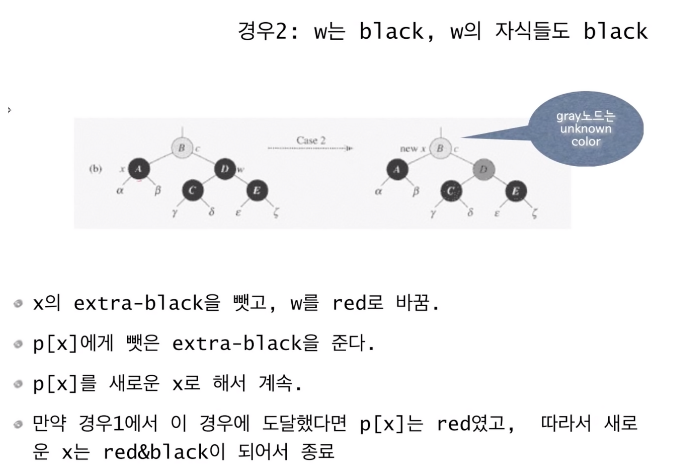
case 1이 w 노드가 레드인 경우였다면, case 2, 3, 4는 블랙인 경우다. 그 중에서도 case 2는 w의 두 자식이 모두 블랙 노드인 경우이다.(case 1에서는 w가 레드였으므로 부모 노드는 블랙이어야 했지만, case 2의 경우에는 그런 제약이 없으므로 블랙일 수도 있고, 레드일 수도 있다.
이 경우에는 x로부터 extra-black을 빼앗고, w를 레드로 바꾼다. 그리고 부모 노드인 B에게 extra-black을 주는데, B가 원래 레드 노드였다면 그냥 블랙 노드로 바꾸고 끝내면 되는 일이지만, 원래 블랙 노드였다면 B노드도 extra-black 노드가 되므로 B노드를 x로 삼아 다시 case 2를 반복한다.
DELETE FIXUP case 3

case 3은 w는 블랙이고 w의 왼쪽 자식이 레드인 경우이다.
이 경우에는 w를 레드로 바꾸고, w의 왼쪽 자식을 블랙으로 바꾼다. 그리고 w에 대해서 right-rotation을 하게 되면 오른쪽 그림처럼 된다. 이 경우는 case 4에 해당하므로 case 4를 진행하면 된다.
DELETE FIXUP case 4
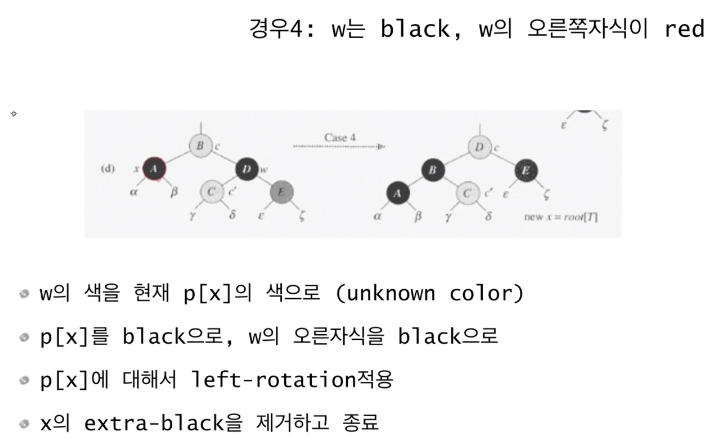
case 4는 w는 블랙이고 w의 오른쪽 자식이 레드인 경우이다.
이 경우는 w의 색을 x의 부모의 색으로 바꾸고, x의 부모와 w의 오른쪽 자식을 검은색으로 바꾼다. 그리고 x의 부모를 기준으로 left-rotation을 진행하면 오른쪽 그림처럼 된다. 그리고 나서 x의 extra-black을 제거하면 종료된다.

case 1, 3, 4의 경우에는 두 스텝 이내로 조정을 마칠 수 있는 반면, case 2는 경우에 따라 2가 반복될 수도 있고, 6이 될 수도 있고, 5, 7, 8이 되기도 한다. 처음부터 case 2에 도착한 경우에는 이렇게 복잡한 반면, case 1을 거쳐 2로 가는 경우는 한번에 마친다.(case 1에서 2로 가는 경우에는 x의 부모가 레드 노드이기 때문이다)
DELETE FIXUP pseudo code
RBTREE-DELETE-FIXUP(T, x)
1 while x != root[T] and color[x] == RBTREE_BLACK
// 경우 1, 2, 3, 4
2 do if x == left[p[x]]
3 then w ← right[p[x]]
// 경우 1 : w가 레드인 경우
4 if color[w] == RBTREE_RED
5 then color[w] ← RBTREE_BLACK
6 color[p[x]] ← RBTREE_RED
7 LEFT-ROTATE(T, p[x])
8 w ← right[p[x]]
// 경우 2 : w가 블랙이고 자식들도 블랙인 경우
9 if color[left[w]] == RBTREE_BLACK and color[right[w]] == RBTREE_BLACK
10 then color[w] ← RBTREE_RED
11 x ← p[x]
12 else
// 경우 3 : w가 블랙이고 왼쪽 자식이 레드인 경우
13 if color[right[w]] == RBTREE_BLACK
14 then color[left[w]] ← RBTREE_BLACK
15 color[w] ← RBTREE_RED
16 RIGHT-ROTATE(T, w)
17 w ← right[p[x]]
// 경우 4 : w가 블랙이고 오른쪽 자식이 레드인 경우
18 color[w] ← color[p[x]]
19 color[p[x]] ← RBTREE_BLACK
20 color[right[w]] ← RBTREE_BLACK
21 LEFT-ROTATE(T, p[x])
22 x ← root[T]
// 경우 5, 6, 7, 8
23 else (same as then clause with "right" and "left" exchanged)
24 color[x] ← RBTREE_BLACK
RB-DELETE-FIXUP 함수의 파라미터인 x는 삭제한 노드의 자식 노드이다.
- line 1) x가 루트 노드이거나 x가 레드 노드라면 line 24처럼 x를 블랙 노드로 만들고 끝내면 된다.
- line 2~22) case 1, 2, 3, 4 즉, x가 부모의 왼쪽 노드
- line 3) x의 부모의 오른쪽 자식 노드(형제 노드를) w로 둔다.
- line 4) w가 레드인 경우 즉, case 1
- line 9) w의 왼쪽, 오른쪽 자식이 모두 블랙인 경우 즉, case 2
- line 13) w의 왼쪽 자식이 레드이며, 오른쪽 자식은 블랙인 경우 즉, case 3
- line 11, 22) line 11에 걸려서 x를 x의 부모 노드로 만든다면 while 문을 계속 돌고, line 22에 걸려서 x를 루트 노드로 하면 while 문에서 빠져나간다.
- line 23) case 5, 6, 7, 8 즉, x가 부모의 오른쪽 노드
DELETE 시간복잡도
BST에서 z 노드를 삭제하는데 이 걸리고, RB-DELETE-FIXUP을 수행하는 데도 이 걸리므로 DELETE의 시간복잡도는 이라고 할 수 있다.
RBTREE 구현 Github 링크
RBTREE
