4.1 On-policy vs Off-policy

Relationship between on-policy & off-policy

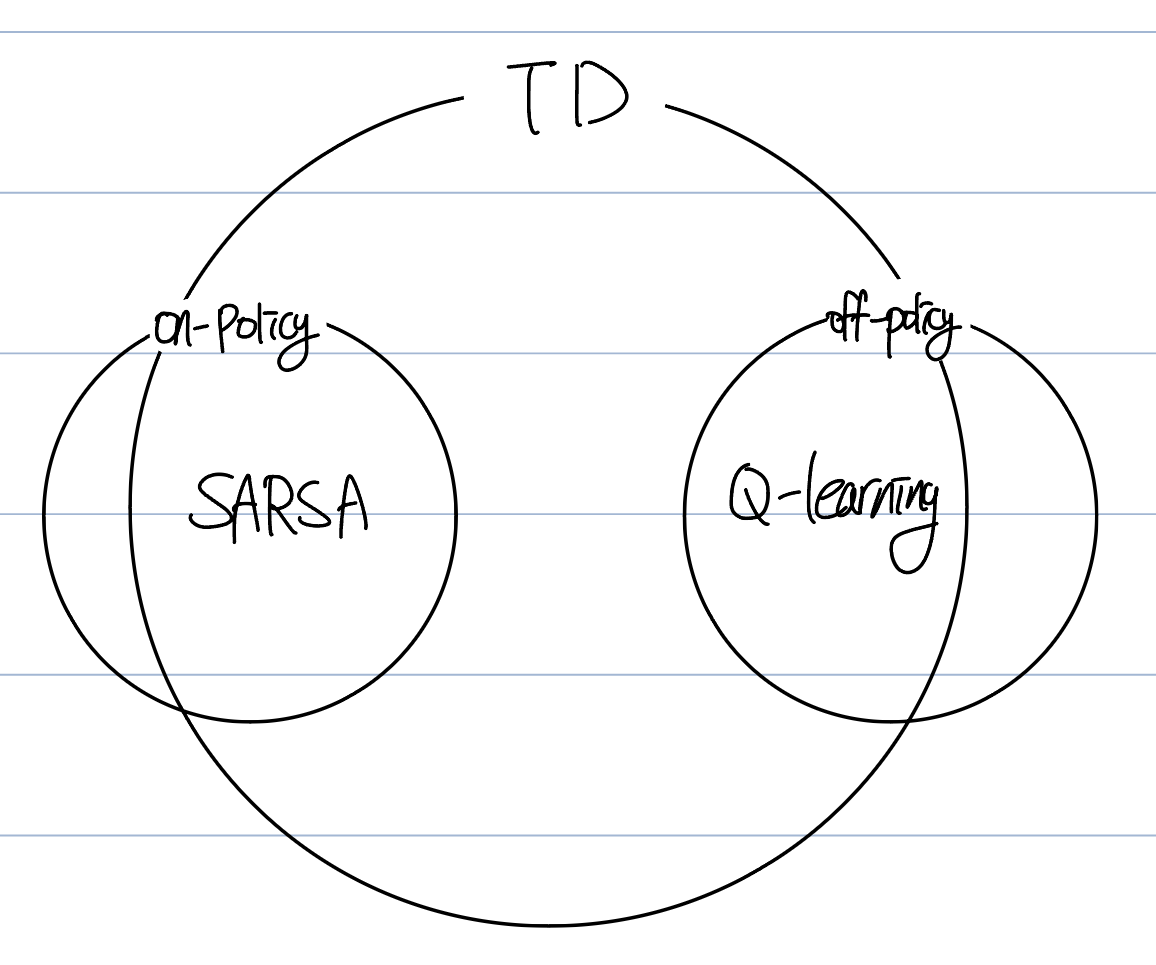
If a behavior policy equals to target policy, we call the policy On-policy. And if they are not equal, then we call the policy Off-policy.

What is behavior policy & target policy?

Recall action value function and TD approximation.

The yellow box is transition probability distribution function. As we have learned in the Bellman equation, we get current action($a_t$) by policy $p(a_t|s_t)$. Then we get next state($s_{t+1}$) by transition pdf(yellow box). We call this policy behavior policy, and also denote as $q(a_t|s_t$).

And the blue box is TD-target(as we’ve learned). TD-target is sampled data from probability distribution, and this probability distribution function is called target policy(The green box).

Since $R_t$ is from $s_{t+1}$, and we need $s_{t+1}, a_{t+1}$ for next Q : $Q(s_{t+1}, a_{t+1})$, the green box should be the target policy, not the yellow box.

In short, the pdf for transition(yellow box, for current action) is from the behavior policy($p(a_t|s_t) = q(a_t|s_t)$), and the policy for next action(green box) is the target policy. In the previous lecture, we applied same policy for transitions, actions. But we separate behavior and target policy at the off-policy. Why do we do this?

Why off-policy?

off-policy has several advantages.

1. The target policy can be determined by human designers or other agents. This flexibility allows the algorithms to utilize probability distributions that have been proven effective by other algorithms.
2. Thanks to Advantage 1, we can apply the target policy as the optimal policy (greedy). Even if the agent operates using the behavior policy $q$, we assume that future actions (under the target policies) should follow the optimal policy.
   To be specific, the agent actually use $q$ in every action, but assume every future actions to be optimal when updating $Q$.
   Therefore, by having the agent explore repeatedly with the optimal policy, we can obtain the sample, known as the TD-target.
3. The primary advantage of off-policy learning is the ability to re-evaluate. As we update the Q-values, the target policy also improves. Consequently, the post-update target policy diverges from its previous state. This means that even if the agent takes the same action (guided by the behavior policy), its assessment changes over time. Essentially, this dynamic enables re-evaluation. Such re-evaluation prompts the agent to reflect on its actions and discern which ones are more effective.
   In on-policy learning, the target policy and behavior policy are identical, resulting in a static TD-target. In contrast, with off-policy learning, as the target policy gets refined, we obtain an enhanced TD-target, leading the agent to continually reassess its actions.