
알고리즘 주차가 끝났다.
근데 곰곰히 생각해보니까 1년전에 알고리즘 풀었던게 머리에서 지워진 경험이 있었다.
그렇기 때문에 알고리즘 주차가 끝나더라도 계속해서 백준 문제를 풀어야 겠다고 생각했다.
하지만 무작정 풀기만 한다면 또다시 머리에서 지워질까봐 엄청 무서웠는데
그래서 따로 글을 작성하기로 했다.
브론즈 문제 풀면서 대충 답 나오는건 건너뛰고
계속 생각해야되고 처음 보는 알고리즘만 작성하기 때문에
기본 알고리즘은 개발일지 1~4주차를 참고하는게 좋을 것 같다.
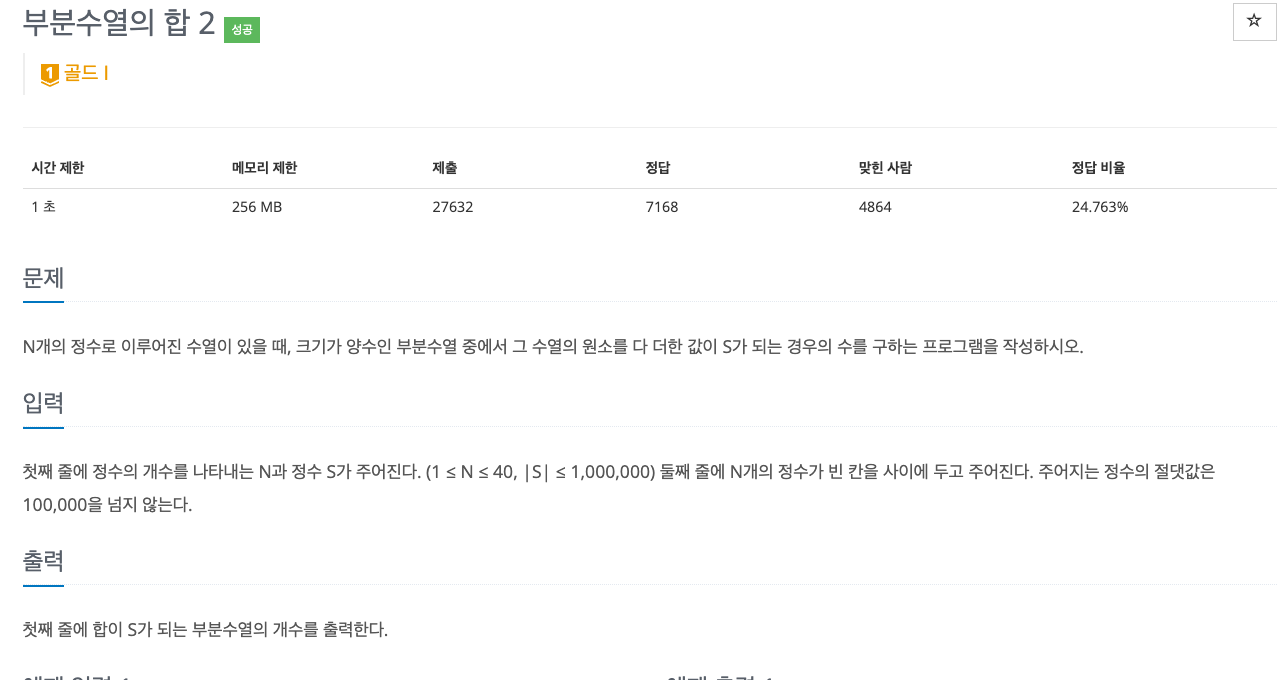
백준 1208 부분수열의 합2이다.
https://www.acmicpc.net/problem/1208
슬슬 골드 상위권 문제들은 메모리와 시간 압박을 엄청 쌔게 준다.
이 문제를 단순히 부르트포스를 쓰게 되면 O(2^n)이 나오기 때문에 대책이 필요하다.
보통 이럴때 가장 많이 들고오는게 binary search 아니겠는가..!
그래서 이 문제를 풀게 되면 이진탐색을 복습한다는 느낌이 엄청 강하다.
문제의 시간초과에 대해 이해를 하자면
-
어떤 수를 더하면 S가 나오는지 모르기 때문에 부르트 포스를 이용하게 되면 2^N이다.
-
2^n의 특징은 n이 반토막이 났을때 계산량은 엄청나게(생각보다 훨씬 더) 심하게 차이난다.
-
그래서 우리는 2^N -> 2*2^(N/2) 로 바꾸는 알고리즘을 짤 것이다.
이것을 다른말로 설명한다면
-
2^40 = 1.0995116e+12 (대충 조단위)
-
2^20 = 1048576
그렇다 우리는 1시간 걸리던걸 1초도 안되서 풀 수 있게 되는 것이다.
자, 하나의 수열을 생각해보자.
우리는 이 수열의 부분집합들을 하나하나 계산해서 계산을 할려고 하면 2^N이 나올것이다.
그래서 우리는 이 수열을 반으로 나눠서 부분집합을 만들것이다.

그런데 우리가 여기서 궁금한것은 멀쩡한 수열을 반토막내서 붙이는게 왜 정답과 같아지는 것인지 이다.
예시를 한번 봐 보자.
arr = [1,2,3,4,5,6]
우리가 찾는 부분집합의 합 = 14
그렇기 때문에 여기에 해당하는 부분집합을 한번 생각해 보면
[1,2,5,6] , [2,3,4,5] , [3,5,6]
이렇게 3개가 나올 것이다.(더나오는지는 모르겠다)
그럼 이제 수열을 잘라서 생각해보자.
arr1 = [1,2,3]
arr2 = [4,5,6]
이렇게 될 것이다.
이 수열들을 부분집합으로 만들어 보자.
sub1 = [[0] , [1] , [2] , [3] , [1,2] , [1,3] , [2,3] , [1,2,3]]
sub2 = [[0] , [4] , [5] , [6] , [4,5] , [4,6] , [5,6] , [4,5,6]]
이렇게 되고, 이 부분수열들을 각각의 합을 구하면
sub1 = [0 , 1 , 2 , 3 , 3 , 4 , 5 , 6 ]
sub2 = [0 , 4 , 5 , 6 , 9 , 10 , 11 , 15]
가 될 것이다.
그렇다면, sub1과 sub2의 값을 하나씩 더해서 14가 되는 수는?
3 + 11
3 + 11
5 + 9
이 될 것이다.
근데 잘 생각해보면...
5 , 9 , 11 , 3 모두 부분수열들의 합을 더해서 나온 것들이 아닌가?
그렇다면..
3 = [1 , 2]
3 = [3]
11 = [5 , 6]
5 = [2 , 3]
9 = [4 , 5]
이렇게 나오지 않는가?
그런데 위에서 우리가 나올 수 있는 3가지 수열이
[1,2,5,6] , [2,3,4,5] , [3,5,6]
이라 하였고
5 + 9 = [2 , 3] + [4 , 5]
3 + 11 = [1 , 2] + [5 , 6]
3 + 11 = [3] + [5 , 6]
이 되지 않는가?

여기까지 읽었으면 뭔가 오오~ 하는 생각이 들 것이다.
그렇다
우리는 수열을 반으로 나눈 후, 각각의 수열을 구해서
그 수열의 부분집합의 값을 더해도 원하는 결과를 얻을 수 있는 것이다!!
이제 소스코드를 보면서 어떻게 구성이 되나 살펴보자.
N, S = map(int, sys.stdin.readline().split())
arr = list(map(int, sys.stdin.readline().split()))-> 수열을 받는 부분
arr1 = arr[:ceil(N / 2)]
arr2 = arr[ceil(N / 2):]
sub1 = []
sub2 = []
for number in range(len(arr1) + 1):
for sub in combinations(arr1, number):
sub1.append(sum(sub))
for number in range(len(arr2) + 1):
for sub in combinations(arr2, number):
sub2.append(sum(sub))->수열을 반/반으로 나눈 후 각각의 combination 수열을 만들어주는 부분
sub1.sort()
ans = 0
for i in sub2:
sum_ = S - i
count = bisect_right(sub1, sum_) - bisect_right(sub1, sum_ - 1)
ans += count
if S == 0:
ans -= 1
print(ans)-> sort를 사용해서 sub1을 정렬해주고(이진탐색을 사용하기 위해)값을 찾아서 정답을 구하는 부분

