
느슨해진 알고리즘 공부 마지막문제에 갑자기 핵폭탄이 터졌다.
도전? 이라고 적힌 문제였는데 진짜 이거때문에 거의 12시간 가까이 붙어서 이게 뭔가 하고 계속 보니까 정신이 나갈것 같았다.(솔직히 일요일이라서 집중력이 낮아지긴 했다.)
근데 이걸 그냥 머리로만 이해할려고 하니 이해도 잘 되는것도 아니고 나중에 까먹을까봐 너무 억울해서 글로 정리를 해 볼려고 한다.
지금 반쯤 이해한 상태로 글을 쓰고 있기 때문에 이게 잘 설명할 수 있을지도 모르겠고 긴가민가 나도 내가 뭘 하고싶은지 뭘 할수있는지 잘 모르겠다.
그렇기 때문에 참고만 하고 이 글이랑 다른 글이 다르다면
진짜 잘하는 사람꺼 보거나 위키로 교차검증을 하는걸 추천한다.
그래서 뭐할때 쓰는거임?
https://www.acmicpc.net/problem/9249
백준 9249번 최장 공통 부분 문자열 문제이다.
실버 ~ 골드 문제와는 다르게 알고리즘 이해하는데도 한참 걸렸다.
문제를 간단하게 설명 하자면
두 문자열의 가장 많이 겹치는 문자열을 찾는다는 것이다.
예시로 들어보자면
- 나는초코파이가너무좋아요몽쉘딸기
- 우리모두초코파이가너무좋아요논산딸기
라는 글이 있다고 해보자. 그렇다면 이 두 문장에서
1. 가장 길게 겹치는
2. 공통되는 문자열
은 무엇일까?
- 나는초코파이가너무좋아요몽쉘딸기
- 우리모두초코파이가너무좋아요논산딸기
'초코파이가너무좋아요' 라는 글자가 두 문장 모두에 속해있고,
'딸기'라는 글자도 겹치긴 하지만 '겹치는 가장 긴 문자열'이 아니기 때문에 무시한다.
그럼 한가지 머리에 번뜩이는 생각이 있을 것이다.

아하! 이거 LCS 알고리즘 때려넣으면 한방에 풀리겠구나!
라는 생각을 하고 있으셨다면 정말 자연스럽고 좋은 생각입니다.
하지만
백준에서 그렇게 문제를 호락호락하게 내 줄 리가 없다.
무려 저 문제는 플래티넘3짜리 문제이기 때문이다.

LCS를 포함한 '기초'알고리즘들은 보통 골드 중하위 선에서 다 컷이 난다.
하지만 플래티넘 문제들은 '기본' 개념, 즉 알고리즘에 대해서 어느정도 기초가 잡힌 사람들이 배우는 더 어려운 개념이라는 것이다.(실제로 코딩테스트에서 어려운 문제들은 골드상위~ 정말 어려우면 플래 하위라고 카더라)
그래서 LCP, 맨버- 마이어스 알고리즘이 뭔데?
라고 물어본다면
LCS로는 풀기 싫은(약 20만,20만 문자열 비교 같은거)문제들을 풀기 위해
더 효율적인 방법을 찾은 것이다.
맨버 - 마이어스 알고리즘
일단 이 알고리즘을 이해할려면 먼저 suffix array라는 개념을 알아야 한다.
suffix array는 arr[i]의 모든 접미사를 배열로 나타내 정리한 것이다.
뭔소린지 이해가 안되니까 예시를 보자.
주말내내 지겹게 봤던 banana로 예시를 들어보겠다.
arr[0] = b
arr[0]의 접미사 = anana (banana <- b를 제외한 뒤 문자열)
arr[1] = ba
arr[1]의 접미사 = nana(banana <-ba 를 제외한 뒤 문자열)
이해가 가는가?
이렇게 i를 0부터 arr[-1]까지 앞의 글자를 하나씩 빼서 배열을 만드는 것이다.
이렇게 만들어진 배열을 보자.
접미사
접미사 i
banana$ 1
anana$ 2
nana$ 3
ana$ 4
na$ 5
a$ 6
$ 7글자 뒤에 $를 달아주는 이유는 문자열의 끝부분이(공백이) 사전상(정렬했을때) 앞으로 오게 되기 때문에 정렬에 방해되지 말라고 넣어주는 것이다.
그리고 이걸 오름차순 정렬 해버린다.
접미사
접미사 i
$ 7
a$ 6
ana$ 4
anana$ 2
banana$ 1
na$ 5
nana$ 3
이렇게 배열된 접미사 배열을 A[j]라고 정하자.
그리고 배열을 다시 정리하게 되면
j A[j] 해당하는 접미사
1 7 $
2 6 a$
3 4 ana$
4 2 anana$
5 1 banana$
6 5 na$
7 3 nana$짜잔! 정리가 되었다.
이렇게 정렬된 데이터를 가지고 다른 계산법을 쓰게 되면 우리가 원하는 값을 얻을 수 있다!
하지만 우리는 이러한 계산을 컴퓨터한테 명령하기 위한 알고리즘이 필요하다.
그렇게 해서 나온것이
- 나이브한 알고리즘
- 맨버 마이어스 알고리즘
이 2개가 대표적이다.
하지만 나이브한 알고리즘은 시간복잡도가 O(n^2 log n) 이기 때문에
문자열이 10만개쯤 넘어가면 컴퓨터가 죽을려고 한다. 즉 그럴바에는 LCS를 쓰는게 맞다.
하지만 맨버 마이어스 알고리즘은 다르다. 무려 시간복잡도가 O(n log n) 이기 때문에 무려 상수항이 n이다! log n 은 곱해 봤자 그렇게 크지 않기 때문에
장난아니게 빠르다!
그래서 여기서 강조할 것은
- 맨버 마이어스/나이브한은 suffix array를 이용하기 위한 전처리 과정이라고 생각하면 된다.
- 맨버 아이어스/나이브한은 속도 차이가 엄청나다
라고 알면 되겠다.
나처럼 맨버 마이어스/나이브한/suffix array가 전부 다른것이라 생각해 헛시간 보내지 않았으면 한다.
맨버 - 마이어스 알고리즘
여기 블로그가 설명이 잘 나와있다.
https://codable.tistory.com/14
이 알고리즘은 suffix array를 이용한 계산을 어떻게 빠르게 구할 수 있을까 라는 고민에서 나온 알고리즘이다.
우선 위키의 설명을 보자.
- 문자열 S 의 접미사들을 첫번째 글자와 두번째 글자에 대해 사전순으로 정렬한다.
- 정렬된 순서를 바탕으로 랭크를 부여한다.
- 접미사의 특성을 이용하여 부여된 두개의 랭크를 기준으로 정렬한다. (비교 범위가 두배가 된다.)
- 2로 돌아간다.
뭔가 생소한 글자가 나왔다. 우리가 중점으로 볼 것은 '랭크'와 '비교 범위가 2배가 된다'이다.
랭크는 정렬을 위해 정한 일정한 기준으로, 어떤 접미사에서 접두사를 빼도 접미사인 성질을 응용한 것이다. Manber-Myers 알고리즘에서는 각 단계마다 접미사에 랭크를 부여하고, 랭크를 기준으로 정렬을 한다. k번째 단계에서 사용되는 랭크는 접미사의 앞에서 2^k-1 글자의 순서 정보를 담고 있다.
라고 위키에 나와있다.
이해가 안되면 그냥 넘어가자. 한번만 정독하면 된다.
일단 배열을 해 보자.
배열의 규칙은 다음과 같다.
- 비교하는 범위에 해당하는 문자가 없으면 -1을 부여한다.
- 정렬된 배열에서 비교하는 범위에 대해 이전 인덱스(j-1)와 같으면 같은 랭크를, 다르면 1을 더한 랭크를 부여한다.
문자열 S = banana를 첫번째 문자에 대해 정렬한 뒤 첫번째 랭크를 부여한 결과는 다음과 같다.
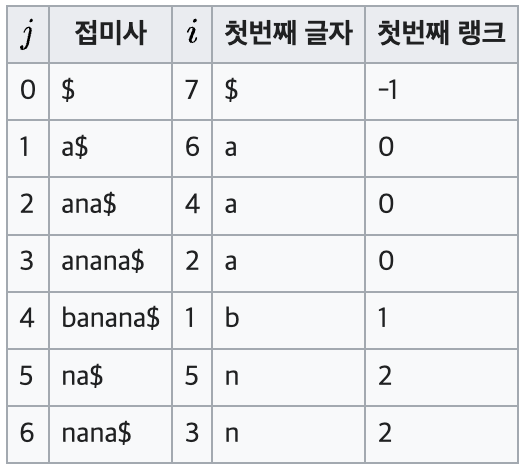
이런 배열이 나온다.
자, 첫번째 랭크를 위에서 부터 한번 봐보자.
기준 글자는 a이다.
그래서 a의 첫번째 랭크는 0이고, 공백인 $는 -1을 줬다.
그 후, b,n은 차례로 2,3을 줬다.(배열 규칙 2번)
이제 다음 랭크를 구해보자.
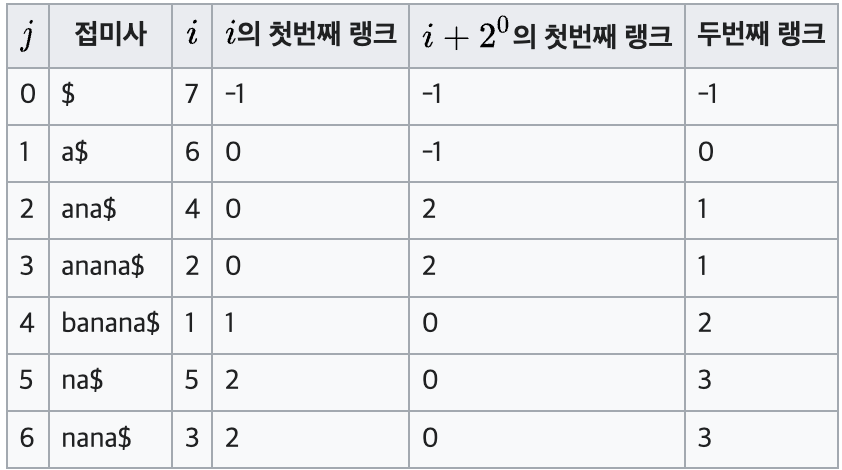
두번째 랭크까지 나왔다!
여기서 많은사람들이 혼란에 빠진다.
- 정렬된 배열에서 비교하는 범위에 대해 이전 인덱스(j-1)와 같으면 같은 랭크를, 다르면 1을 더한 랭크를 부여한다.
라고 했는데 랭크는 무슨 기준으로 계산하는거야?
아니라면 축하한다. 난 여기서 하루를 날렸다.
우선 한 부분을 보자.

뭔지 알겠는가?
j = 0,1 행의 일부를 가져온 것이다.
정말 간단하다.
- j = 0의 첫번째 랭크 vs j = 1 의 첫번째 랭크
- j = 0의 i+2^0의 첫번째 랭크 vs j = 1의 i+2^0의 첫번째 랭크
이걸 비교해서 둘 중 하나라도 틀리면
j = 0 의 두번째 랭크 값에서 +1 한게 j = 1 의 두번째 랭크 값이다.
이것이 햇깔리는가? 그럼 수식으로 써 보겠다.
- -1 != 0 or -1 != -1 => 두번째랭크[1] = 두번째랭크[0] +1
이렇게 된다.
위의 글자에 해당되는 수를 하나하나 대입한거다.
밑으로가도 다 똑같은소리 하고 있는거다.
밑도 똑같다.

- 0 != -1 or 0 != 2 => 0+1 = 1
이렇게 되는것이다.
그냥 이렇게 쭉쭉 적어나가면 되는건데
설명에 문제가 있다.
- 정렬된 배열에서 비교하는 범위에 대해 이전 인덱스(j-1)와 같으면 같은 랭크를, 다르면 1을 더한 랭크를 부여한다.
이 글만 보면 저게 저소린지 모른다는 것이다...
어쨌든 이런식으로 쭉쭉 채워 나가게 되면
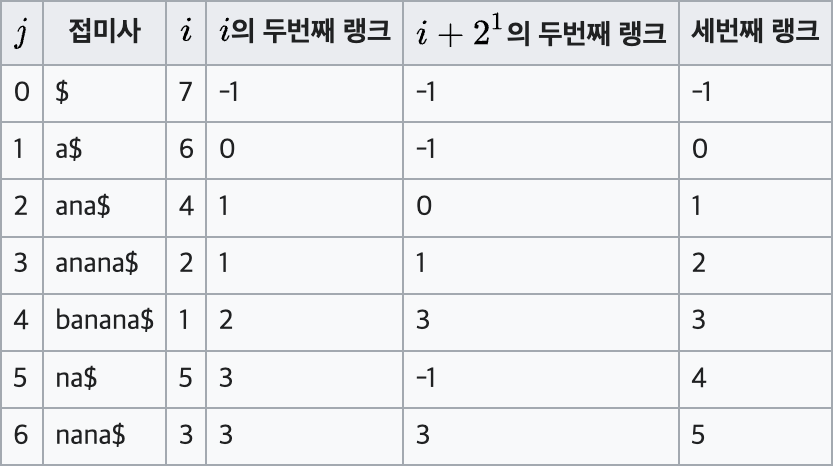
짜잔!
정렬 순서대로 세번째 랭크가 완성이 되었다!

근데 구하고 보니까 딱 이소리가 나온다.
아니 그냥 sort한 index 값으로 하면 되는거아님?
왜 굳이 이걸 따로 랭크값을 매기는거임?
이라는 반응이 나도 나왔기 때문이다.
다시 한번 정리를 하자면
- suffix array를 구하는 방법이 2개가 있다.
- 단순 sort 쓰다가는 컴퓨터가 죽는다.
- 근데 나이브이한 알고리즘은 겁나 느려서 쓰기 힘들다.
- 맨버 - 마이어스 알고리즘의 작동 원리가 랭크를 쓰는 방법이다.
- 이렇게 구한 배열은 LCP를 쓰기 위한 전처리 과정이다.
실제로 이 다음 LCP를 계산할 때 랭크값은 여기까지만 쓰고, 배열의 ord값(문자의 번호 -> 아스키 코드 번호라고 생각하면 편함)을 쓰게 된다.
그렇다면 다음 주제인
왜 비교 범위가 두배씩 늘어나는가?
에 대한 해답은 여기서 잘 적어줬다.
https://m.blog.naver.com/zxwnstn/221573201666
이제 다음 방법으로 넘어가자.
LCP
드디어 전처리 과정을 넘어 우리가 해야하는 주제로 돌아왔다.
LCP는 longest common prefix array,
즉 최장 공통 접두사 배열 이라고 한다.
여기서 우리는 비교를 할 때 어떻게든 시간을 줄여야 하는데,
이때 사용되는 것이 kasai 알고리즘이다.
kasai 알고리즘은 짧게 정리하면 이렇게 표현할 수 있다.
두 문자열을 비교할때
- A = EC(1)F
- B = EC(1)P
이때 C(1) 은 공통된 배열이다.(ex/ 초코파이가너무좋아요 -> 위의 예시)
공통접미사의 길이는 K이다.
이런 상황을 봤을때, A와 B의 앞 글자를 하나씩 때보자.
- A' = C(1)F
- B' = C(1)P
보이는가? A와 B 모두 하나씩 때도 뒤의 글자가 같다!
그렇기 때문에 공통접미사의 길이는 K-1 이상이라는 소리다.
이걸 이용해서
우리는 공통 접미사의 계산 내용을 계속 이용할 것이다.
이렇게 쭉쭉쭉 이용하다보면?
하나씩 다 대입해서 푸는 방법보다는 훨씬 빠른 시간 안에 풀 수 있다.
마치 DP의 bottom - up 방식과 같다.
어찌어찌 하기는 했는데 이걸 다른사람한테 말로 설명하라고 하면?
좀 불안하긴 하다.
만약에 이 글을 보는 여러분들은 진짜 고통받지 않기를 바라지만
이 글이 그렇게 도움이 될까? 라는 생각도 든다.

