SSC
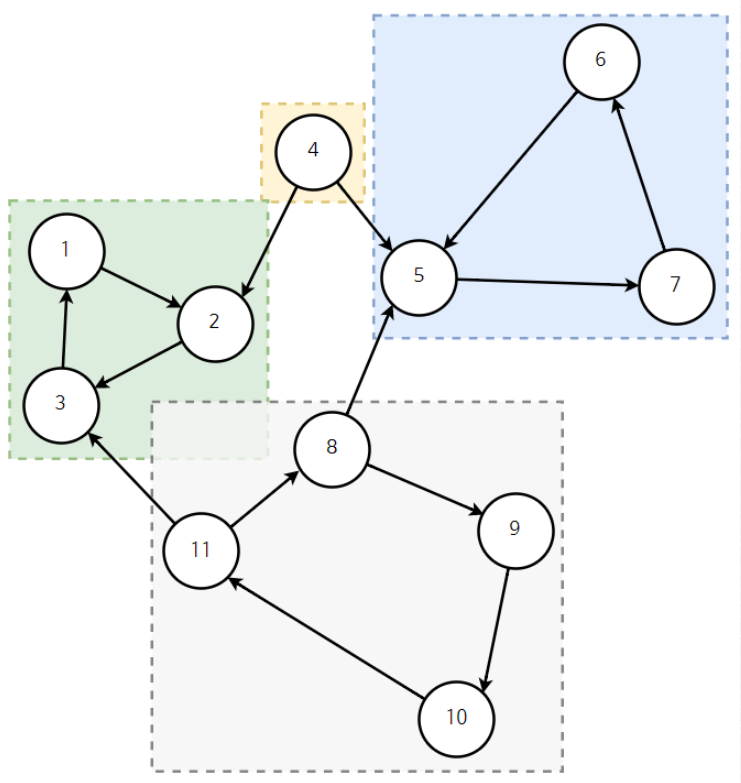
SSC : Strongly Connected Component
강한 결합 요소는 그래프 안에서 강하게 연결된 정점 집합을 의미한다.
위 그림에서 보면 ( 1 , 2 , 3 ) , ( 6 , 7 , 5) , ( 8 , 9 , 10 , 11 )은
서로가 서로를 가르키며 순환하는 구조를 가지고있다.
이러한 노드들을 SSC라고 한다.
SSC를 구하는 방법은 크게 2가지가 있다.
- Tarzan
- Kosaraju's
하지만 이 글에서는 Tarzan 알고리즘만 설명을 할 것이다.
두개의 차이점을 적어보자면
Tarzan은 dfs 한번으로 모든 정보를 얻을 수 있는 반면에,
Kosaraju는 한번 dfs를 한 후 역행 dfs를 한번 더 해야 한다는 단점이 있다.
그렇기 때문에 우리는 효율적인 Tarzan 알고리즘을 공부해야 한다.
Tarzan
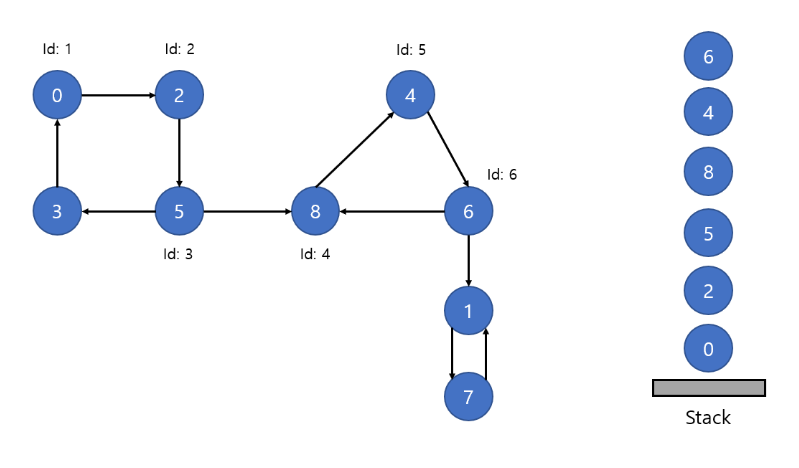
Tarzan 알고리즘은 stack을 이용한 알고리즘이다.
def SCC(node):
global idx , scc_num
visit[node] = idx
root = idx
idx += 1
stack.append(node)
for next in arr[node]:
if not visit[next]:
root = min(root,SCC(next))
elif not check[next]:
root = min(root,visit[next])
if root == visit[node]:
while stack:
top = stack.pop()
check[top] = 1
scc_idx[top] = scc_num
if node == top:
break
scc_num += 1
return root다음과 같은 절차를 따른다.
-
노드를 검사한다.
-
만약 방문하지 않은 노드면, SCC를 돈다.
-
방문한 노드라면, check를 확인하고 루프를 빠져나온다.
-
만약 root가 visit[node]라면(사이클에 처음 들어온 노드)
-
사이클의 노드 들을 모조리 pop하며 check, scc_idx를 갱신한다.
말로보면 참 편한 알고리즘인데.. 구현하는게 엄청나게 빡세다..
2-SAT
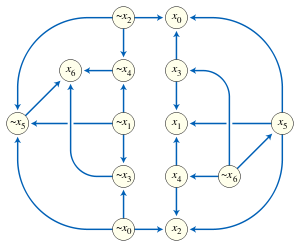
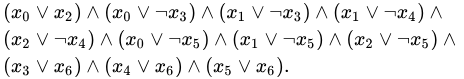
2-SAT 문제는 충족 가능성 문제 중 하나이다.
충족 가능성 문제는 boolean으로 문제의 식을 충족시킬 수 있을때,
각 변수가 True, False 중 하나를 선택해 전체 식을 True로 만들 수 있느냐 라는 문제이다.
간단하게 말해서 2-SAT 문제는 ( X , Y ) 에 OR 연산을 하고, 이러한 행들이 전부 True가 되게 하면 된다는것이다!!
물론 여기서는 notX도 있기 때문에 단순히 전부 True를 대입한다 하더라도 전체식이 False가 나올 수 있다.
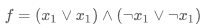
다음 그림으로 예제를 본다면
-
왼쪽 행은 X1 과 X1에 OR 연산을 한 것이고
-
오른쪽 행은 notX1과 notX1에 OR 연산을 한 것이다.
즉, 위 식은 X1에 어떠한 값을 집어넣더라도 항상 False가 나온다는 것이다.
이 문제도 개념 자체는 간단하다.
나올 수 있는 경우의 수는 2가지 밖에 없기 때문이다.
- X OR Y
- notX OR Y
(not - not은 1,2번과 같음으로 패스)
이렇게 될때, 어떤 명제가 가능해지는지 살펴보자.
X OR Y
X가 True이라면, Y는 어떠한 것이 나와도 상관없다.
X가 False라면, Y는 True가 나와야 한다.
즉, X -> notY , Y -> notX 가 되는 것이다.
물론, X -> Y도 되긴 할 것이다. 하지만 X,Y가 모두 True이여야만 참이 됨으로. X -> Y는 항상 참이라고 할 수 없으니, 명제가 아니다.
not X OR Y
위와 마찬가지로 어떤 값을 넣더라도 항상 참이되는 명제를 구해야 한다.
즉, X -> Y , Y -> X 가 되는 것이다.
이것을 알고리즘으로 구현하면 된다.

