
또 쉬워보인다고 물었다가 3시간이 날아갔다.
백준 18809 Gaaaaaaaaaarden
https://www.acmicpc.net/problem/18809
시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율
2 초 512 MB 5452 2510 1586 43.298%
문제
길고 길었던 겨울이 끝나고 BOJ 마을에도 봄이 찾아왔다. BOJ 마을에서는 꽃을 마을 소유의 정원에 피우려고 한다. 정원은 땅과 호수로 이루어져 있고 2차원 격자판 모양이다.
인건비 절감을 위해 BOJ 마을에서는 직접 사람이 씨앗을 심는 대신 초록색 배양액과 빨간색 배양액을 땅에 적절하게 뿌려서 꽃을 피울 것이다. 이 때 배양액을 뿌릴 수 있는 땅은 미리 정해져있다.
배양액은 매 초마다 이전에 배양액이 도달한 적이 없는 인접한 땅으로 퍼져간다.
아래는 초록색 배양액 2개를 뿌렸을 때의 예시이다. 하얀색 칸은 배양액을 뿌릴 수 없는 땅을, 황토색 칸은 배양액을 뿌릴 수 있는 땅을, 하늘색 칸은 호수를 의미한다.
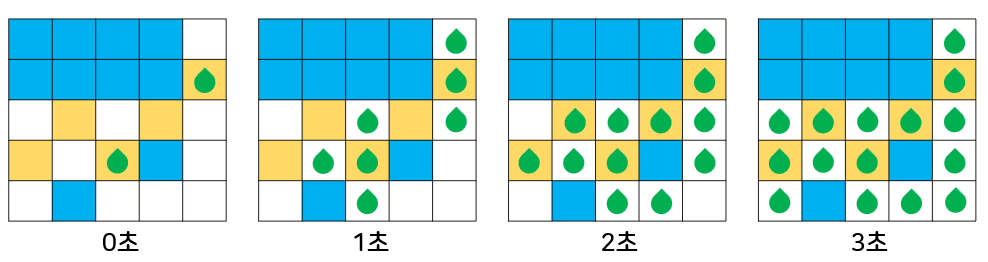
초록색 배양액과 빨간색 배양액이 동일한 시간에 도달한 땅에서는 두 배양액이 합쳐져서 꽃이 피어난다. 꽃이 피어난 땅에서는 배양액이 사라지기 때문에 더 이상 인접한 땅으로 배양액을 퍼트리지 않는다.
아래는 초록색 배양액 2개와 빨간색 배양액 2개를 뿌렸을 때의 예시이다.
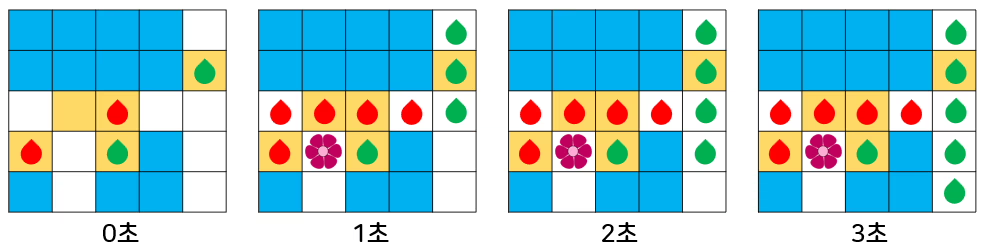
배양액은 봄이 지나면 사용할 수 없게 되므로 주어진 모든 배양액을 남김없이 사용해야 한다. 예를 들어 초록색 배양액 2개와 빨간색 배양액 2개가 주어졌는데 초록색 배양액 1개를 땅에 뿌리지 않고, 초록색 배양액 1개와 빨간색 배양액 2개만을 사용하는 것은 불가능하다.
또한 모든 배양액은 서로 다른 곳에 뿌려져야 한다.
정원과 두 배양액의 개수가 주어져있을 때 피울 수 있는 꽃의 최대 개수를 구해보자.
입력
첫째 줄에 정원의 행의 개수와 열의 개수를 나타내는 N(2 ≤ N ≤ 50)과 M(2 ≤ M ≤ 50), 그리고 초록색 배양액의 개수 G(1 ≤ G ≤ 5)와 빨간색 배양액의 개수 R(1 ≤ R ≤ 5)이 한 칸의 빈칸을 사이에 두고 주어진다.
그 다음 N개의 줄에는 각 줄마다 정원의 각 행을 나타내는 M개의 정수가 한 개의 빈 칸을 사이에 두고 주어진다. 각 칸에 들어가는 값은 0, 1, 2이다. 0은 호수, 1은 배양액을 뿌릴 수 없는 땅, 2는 배양액을 뿌릴 수 있는 땅을 의미한다.
배양액을 뿌릴 수 있는 땅의 수는 R+G개 이상이고 10개 이하이다.
출력
첫째 줄에 피울 수 있는 꽃의 최대 개수를 출력한다.
그냥 보면 참 쉬워보인다.
대충 백트래킹같은거 사용해서 배양액 위치 찾고 bfs 돌리면 될거같은데
제한시간이 2초밖에 안된다.
그런데 들어갈 수 있는 최대 크기가 50X50이다.
그게 뭔 말이냐면
50 50 2 2
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
ans = 114
https://www.acmicpc.net/board/view/88389
(테케 출처)
테스트케이스가 이따구로 나온다는 뜻이다.
백트래킹 몇번 써본사람은 감이 오겠지만 저런거 N^2으로 돌렸다가 대충 몇년씩 걸릴것으로 예상이 된다.
그래서 이 문제에서 가장 중요한것은 어떻게 시간복잡도를 최대한 줄일까에 대한 고민이다.
우리는 BFS문제를 아주 만만하게 보고 있고 실제로도 코딩 자체는 골드 1 치고 상당히 간단한 편이다.
하지만 구조를 처음부터 잘 짜지 않으면 디버깅 하루종일 하다가 코드 갈아엎는 불상사가 생기기 때문에 처음부터 잘 짜야 한다.
문제풀이는 간단하다.
-
combination으로 배양액 위치만 찾기
-
그 위치를 받아서 BFS를 위해 deque에 좌표 저장
-
좌표의 위,아래,좌,우 를 확인하면서 같은 시간에 다른 색이 칠해쳤다면 꽃으로 매핑, 아니라면 무시
-
return된 값들 중 최대값을 정답으로 출력
이렇게 구조만 잘 짜면 코딩 자체는 골드 하위권이다.
1. 하지만 combination으로 시간 줄이는 포인트,
2. time을 사용해서 경우의 수 줄이기
이 두가지를 잘 해야 되는 문제이다.
from itertools import combinations
from collections import deque
N , M , G , R = map(int,input().split())
garden = [list(map(int,input().split())) for _ in range(N)]
plant = []
lst = set()
def spread(G , R):
cal = 0
for i in range(N):
for j in range(M):
if garden[i][j] == 2:
plant.append((i , j))
plant_copy = set(plant)
for green in combinations(plant , G):
ground_nogreen = list(plant_copy - set(green))
green_list = list(green)
for red in combinations(ground_nogreen , R):
red_list = list(red)
result = blossom(green_list , red_list)
if cal < result:
cal = result
return cal
def blossom(green_list , red_list):
shadow = [[0 for _ in range(M)] for _ in range(N)]
for i in green_list:
shadow[i[0]][i[1]] = 1
for i in red_list:
shadow[i[0]][i[1]] = 2
print()
for k in shadow:
print(*k , end = '\n')
count = 0
dx = [1 , -1 , 0 , 0]
dy = [0 , 0 , 1 , -1]
location = deque()
for i in range(N):
for j in range(M):
if shadow[i][j] == 1 or shadow[i][j] == 2:
location.append([i , j , 1])
timer = 0
spread = [[0 for _ in range(M)]for _ in range(N)]
while location:
i , j , time = location.popleft()
for k in range(4):
x = dx[k] + i
y = dy[k] + j
if 0 <= x < N and 0 <= y < M and garden[x][y] != 0:
if shadow[x][y] == 0 and shadow[i][j] != 3:
shadow[x][y] += shadow[i][j]
spread[x][y] = time
location.append([x,y,time+1])
elif shadow[x][y] == 1 and shadow[i][j] == 2 and spread[x][y] == time:
shadow[x][y] = 3
count +=1
elif shadow[x][y] == 2 and shadow[i][j] == 1 and spread[x][y] == time:
shadow[x][y] = 3
count +=1
return count
print(spread( G , R))

