첫 다이아 문제 풀이다.
생각보다는 벡터쪽 문제라서 할만은 했지만.. 다른 문제들은 얼마나 어려울지 감조차 잡히지 않는다. 이 문제만 해도 정보 검색하는데만 거의 3시간 넘게 썼었고, 벡터의 길이 계산을 외적/내적을 이용하기 때문에 잠깐의 리마인딩 시간도 필요했다.

일반적인 코딩의 한계점은 여기까지인가? 라는 생각도 든다. 애초에 볼록껍질, 회전하는 캘리퍼스 까지는 데이터가 많이 나왔지만, minimum bounding rectangle은 문제를 검색하지 않으면 모르는 정보였다.

그리고 더욱 힘들었던 것은, direct 11에서 쓰는 물리엔진에 들어가는 충돌 판정에 minimum bounding rectangle이 쓰이고, 이를 3D로 만들어 numpy를 써서 연산하는 툴도 많았다.

하지만 나는 vanilla python 을 사용해야 했기에 외부 라이브러리는 사용하지 못했다...

앞으로 편의상 Minimum Bounding Rectangle은 MBR로 부르겠다.

울타리

시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율
1 초 1024 MB 387 107 58 24.268%
문제
준석이는 목장 N채를 가지고 있다. 각 목장은 좌표평면 위의 점으로 나타낼 수 있다. 두 목장이 같은 위치에 있을 수 있다.

준석이는 모든 목장을 둘러싸는 직사각형 모양의 울타리를 치려고 한다. 직사각형의 변이 x축이나 y축에 꼭 평행할 필요는 없고, 변 위에 목장이 놓여 있어도 된다. 목장의 너비와 높이가 0이여도 된다.

모든 목장을 둘러싸는 울타리를 세웠을 때, 울타리의 최소 둘레를 구하여라.

입력
첫번째 줄에 목장의 수 N(2 ≤ N ≤ 50,000)이 주어진다.

다음 N줄에는 한 줄에 하나씩 목장의 x좌표와 y좌표가 주어진다. 모든 좌표는 절댓값이 2 × 108를 넘지 않는 정수이다.

출력
필요한 울타리의 최소 둘레를 출력한다. 절대/상대 오차는 10−7까지 허용한다.






난생 처음 풀어보는 다이아몬드 4짜리 문제이다.
이 문제가 어려운 이유는 볼록껍질 구하고 회전하며 직사각형 연산을 하는데도 시간이 1초밖에 주어지지 않는다.

즉, O(n^2) 방식으로는 절대 풀리지 않고, O(n) 방식으로 직사각형을 구해야 한다는 말이다.

바로 풀이를 보자.

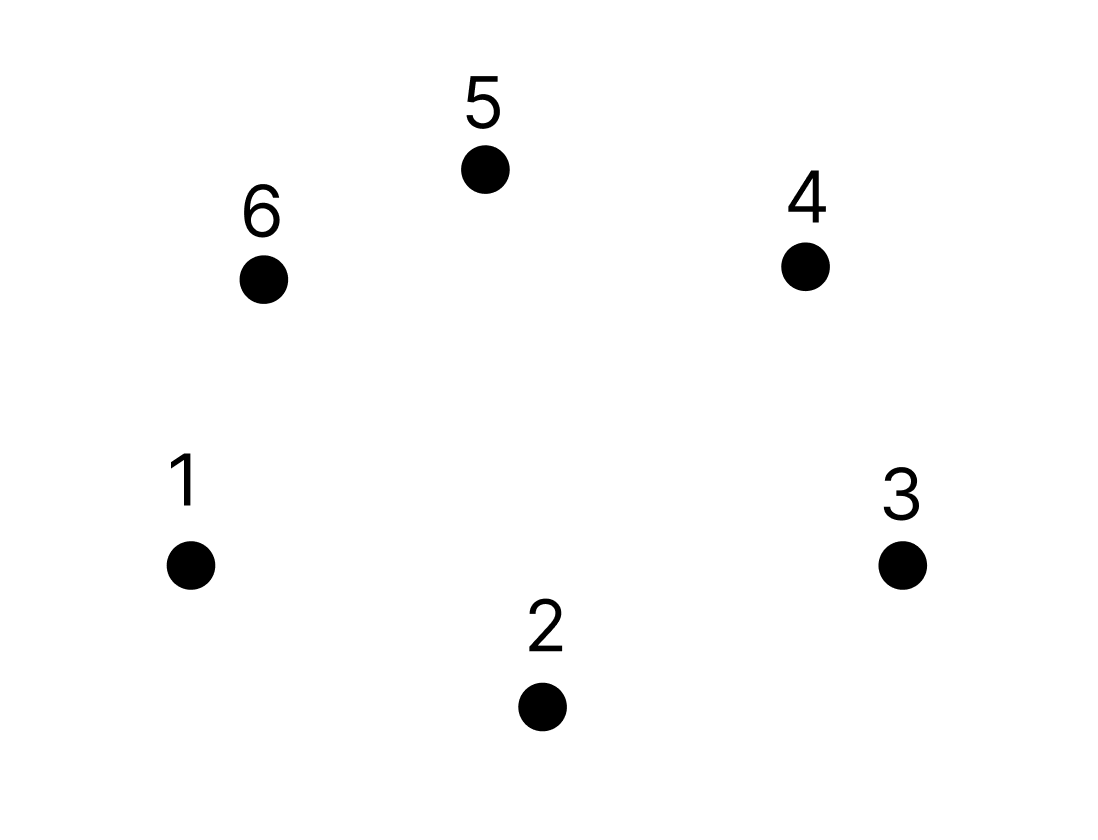
자, 우리는 6개의 점이 2차원 좌표평면 상에 뿌려져 있는걸 볼 수 있다.
여기서, 1-2 선분을 기준으로 MBR을 어떻게 구할 수 있을까?

간단하다! 1-2 선분을 x축으로 잡고, x값이 가장 큰 점, x값이 가장 작은 점, y 값이 가장 큰 점을 잡고 그걸로 rectangle을 만들면 된다.

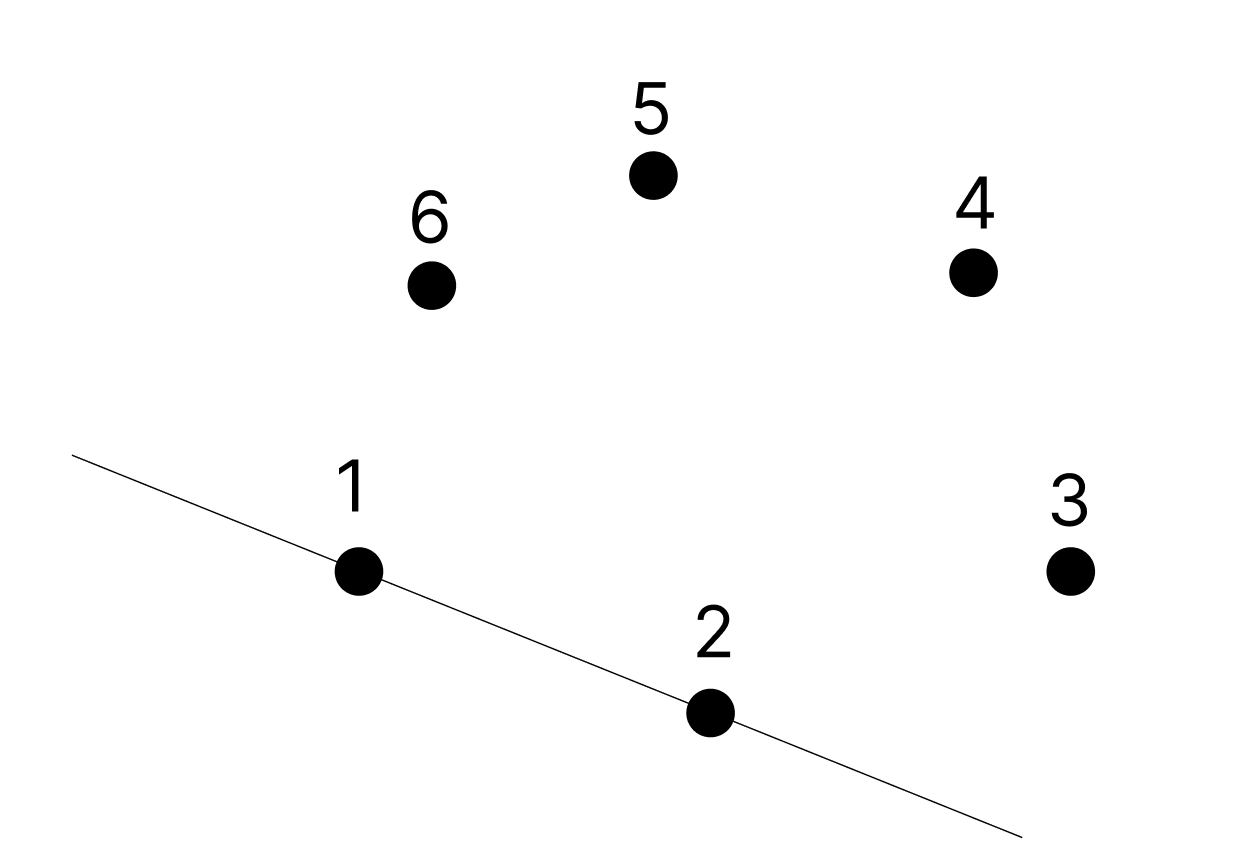
자, 새로운 x축이 되어줄 선을 그었다.
그럼 이제 우리는 1 -> 6번으로 한바퀴 돌았을때 최소값이 나와야 한다.

우선, 직사각형의 우측(2의 오른쪽) 점을 어떻게 잡는지 생각해 보자.

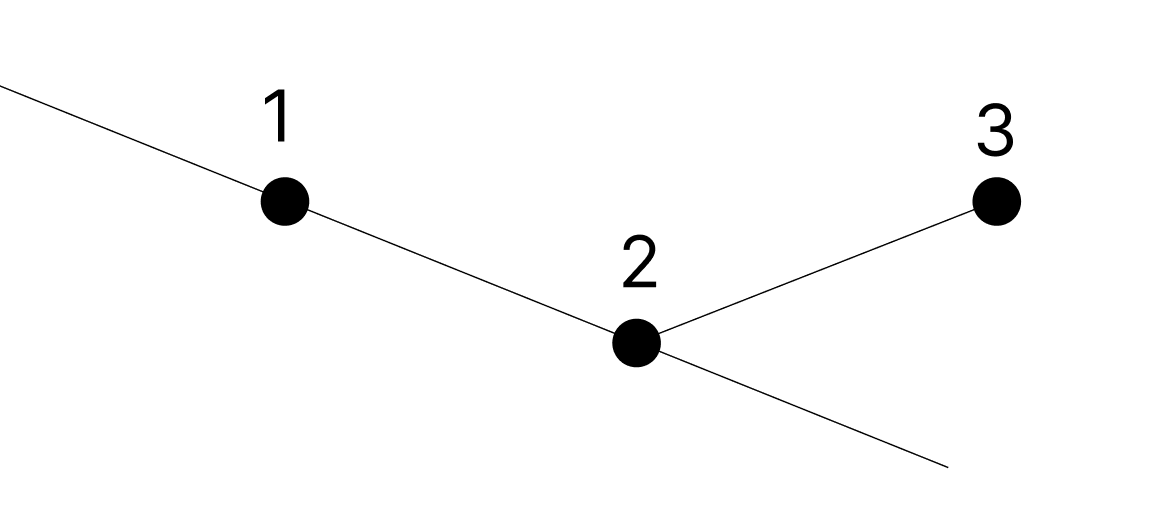
3번을 잡아봤다. 이때, ccw > 0, 내적값도 양수가 된다.
내적이 양수라는 것은 cos값이 90도 이하라는 것이다.
cos값이 90도 이하라는 것은 2번보다 x값이 크다는 소리다.

자 여기서 집중하고 이해해야 하는것이 있다.

• cos값이 90도 이하라서 x값이 커진다 != 실제 좌표의 x값이 커진다.

이것을 명심하여야 한다.
어디까지나 x'축(1-2)의 기준에서 x값이 커진다는 상대적인 x좌표의 증가이기 때문에, x축 기준 x좌표값이 -가 되더라도 x'축 기준에서는 x좌표가 증가할 수 있다.

이것만 이해한다면, 이번 알고리즘은 완벽하게 이해하고 넘어갈 수 있다.

위의 논리를 정확하게 이해하였다면

• 1-2축 기준 y값이 가장 큰 점
• 1-2축 기준 x값이 가장 작은 점

을 모두 구할 수 있다.
이번 문제는 코드적인 부분보다는 기하학 적인 이해도가 필요하기에, 코드 리뷰는 하지 않는다...

다음 문제를 보자.

약수 지우기 게임

시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율
2 초 512 MB 1266 782 674 64.068%
문제
A와 B가 약수 지우기 게임을 한다. 약수 지우기 게임은 두 사람이 즐기는 게임이다.

칠판에 1부터 N까지의 자연수가 적혀 있다. 각 사람은 자신의 턴에 칠판에 적힌 자연수 하나를 지우고, 그 자연수의 약수 중 칠판에 남아 있는 수들을 모두 지운다. 예를 들어, 칠판에 2,3,4,5,6이 적혀 있을 때, 6을 지우면, 그 약수인 2와 3 역시 지워야 한다. 자신의 턴에 숫자를 지우지 않을 수는 없다. 마지막 숫자를 지우는 사람이 지게 된다.

A와 B가 최적의 방법으로 게임을 할 때, 이기는 사람을 출력한다. 게임은 A가 먼저 시작한다.

입력
첫째 줄에 N이 주어진다. N은 1,000,000보다 작거나 같은 자연수이다.

출력
첫째 줄에 A가 이기는 경우 A, B가 이기는 경우 B를 출력한다.

애드훅 이라는 알고리즘이다.
이 애드훅이라는 놈도 참 골때리는것이, 사전적 의미는 다음과 같다.

• 특정한 문제나 일을 위해 만들어진 관습적인 해결책
• 일반화할 수 없는 해결책
• 어떤 다른 목적에 적응시킬 수 없는 해결책

아니 그러니까 정해진 방법도 없고, 증명도 없고, 그저 '그럴거 같다' 라는 관습적인 방법들을 애드훅이라는 이름으로 묶어서 알고리즘 문제를 낸다는 것이다.

위 문제의 풀이도 상당히 간단하다.

N = int(input())
if N == 1:
    print('B')
else:
    print('A')

이게 정답코드 끝이다.

????
나도 문제 풀고난 다음에 어이가 없었지만
애석하게도 위의 코드가 끝이다.

그렇다면 왜 저 코드가 끝인지 생각해 보자.

• 1은 모든수의 약수
• 1을 제외하고 게임을 한다고 가정.
• 1을 제외한 게임에서 B가 무조건 이긴다면, 처음에 1을 지운다.
• 1을 제외했을때 A가 무조건 이긴다면, 그냥 게임을 진행한다.
• 따라서 어떠한 경우에도 A가 무조건 이기는 상황이 나온다.
• 하지만 N = 1일때, 숫자를 지우면 바로 게임이 끝나기 때문에 B가 이기게 된다.

그러니까, N != 1 이라면 선공치는놈이 무조건 이긴다는 소리다.

애드훅은 진짜.. 말로는 형용할수 없는 혐오감이 드는 문제다.