볼록껍질 알고리즘과 이어지는 내용이다.
이번 알고리즘은 이름에서 알 수 있듯이, 길이를 측정하는 기준이 회전을 한다. 무슨말인고 하니, 볼록껍질 list를 탐색하면서 점 사이의 최대값을 구할때 볼록껍질 특성상 원형 도형 위를 회전하며 찾아야 하고 이 때 캘리퍼스로 빙빙 돌면서 측정하는거 같다고 해서 붙여진 이름이다.

일단 문제를 살펴보자.

고속도로

시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율
2 초 (하단 참고) 256 MB 9762 2191 1171 22.519%
문제
n개의 도시를 가진 나라가 있다. 이 나라에서는 도시들 중 가장 먼 두 도시 사이에 직행 고속도로를 놓으려 한다.

고속도로는 시작점과 끝점이 아닌 다른 나라를 통과해도 된다. 즉, n개의 도시 중 유클리드 거리가 가장 먼 두 도시를 찾으려 한다. 모든 도시는 한 평면 위에 있다.

위의 예제에서는 (12,0)의 도시와 (-6,3)의 도시가 가장 먼 유클리드 거리를 갖는다.

도시 n개의 좌표가 주어지면 모든 두 도시 쌍의 거리 중 가장 먼 두 도시를 찾아라.

입력
첫째 줄에 테스트 케이스의 수 T가 주어진다.

각 테스트 케이스의 첫 줄엔 도시의 개수 n이 주어진다. (2 ≤ n ≤ 200,000) 그 후 n줄에 걸쳐 각 도시의 x좌표와 y좌표가 주어진다. (-10,000,000 ≤ x, y ≤ 10,000,000) x, y는 항상 정수이며, 어떤 두 도시가 같은 점 위에 있는 경우는 없다.

출력
테스트 케이스마다 가장 먼 두 점의 좌표를 출력한다.

만일 그 두 점의 좌표가 각각 (x1, y1), (x2, y2)이라면 x1 y1 x2 y2를 출력하면 된다.

가장 먼 거리를 갖는 두 점의 쌍이 여러 개라면 그 중 아무 것이나 출력해도 상관없다.

간단하다. 정석적으로 볼록껍질을 구한 후 회전하는 캘리퍼스 알고리즘을 정확하게 구하면 끝나는 문제다. 하지만 이 문제가 플래티넘2라는 것은 알고리즘 자체가 쉽지 않다는 것을 의미하고 확실한 이해가 필요하다는 것이다.

한가지 주의할점은
인터넷을 뒤져봐도 명확하게 납득할 만한 내용은 나오지 않아 생각을 통해 결론을 낸 설명을 적기 때문에 반례가 나올수도 있다.

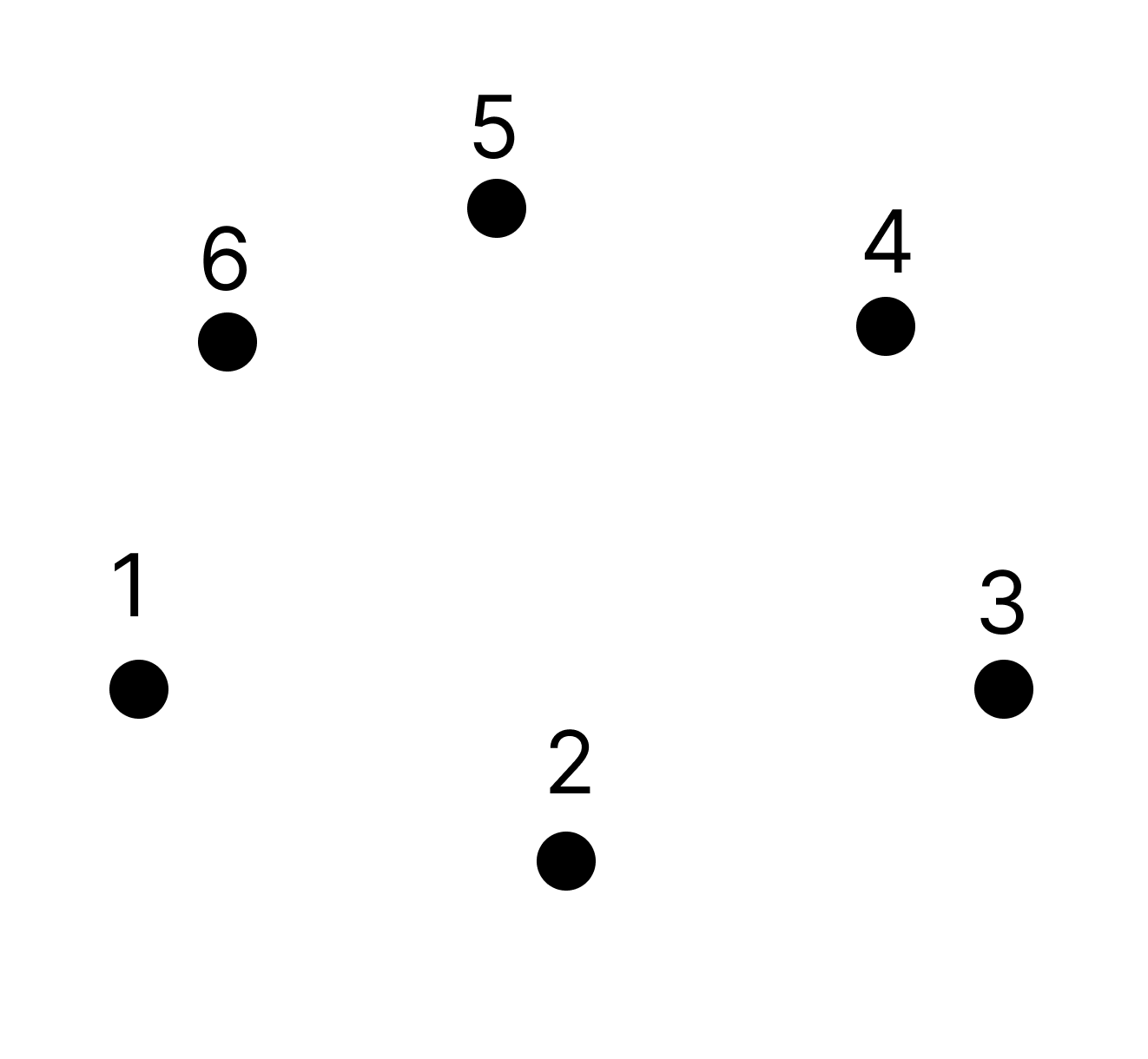
다음과 같은 볼록껍질 집합이 있다고 가정하자. 이때 점 사이의 최대 거리를 구할려면 어떻게 해야할까?

여기서 우리는 중요하게 생각할 점이 있다.

• 볼록껍질들은 원형으로 배치되어 있다.
• 그렇다면 다음 점이 지금 점보다 거리가 어떤지는 알수 있나??

무슨 말인지 이해가 가는가?

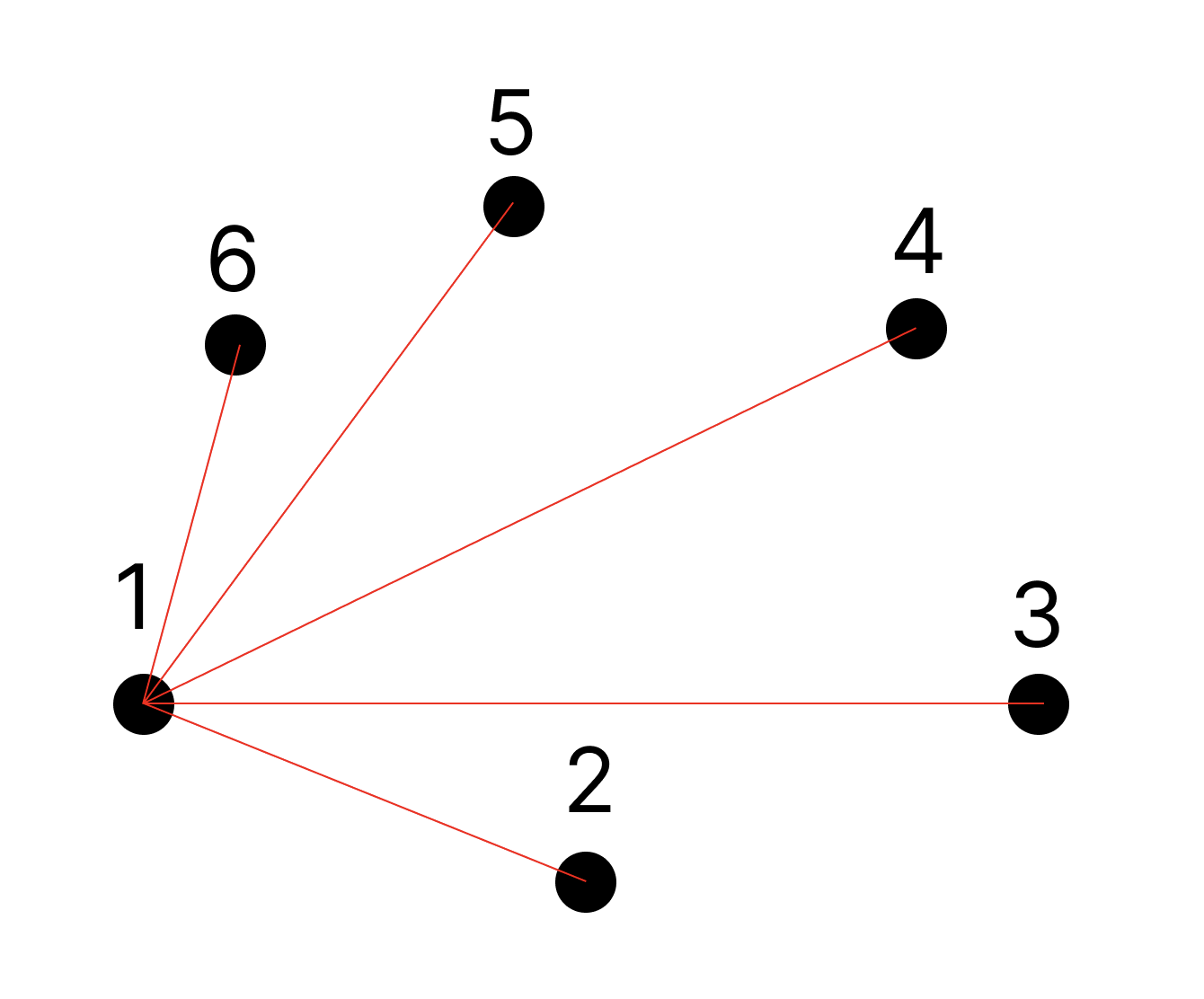
위의 그림에서 우리가 알 수 있는것은
5번 보다 6번이 1번에 가깝다는 것이다.
이것이 왜 중요한지는 다음 그림을 보면서 생각하자.

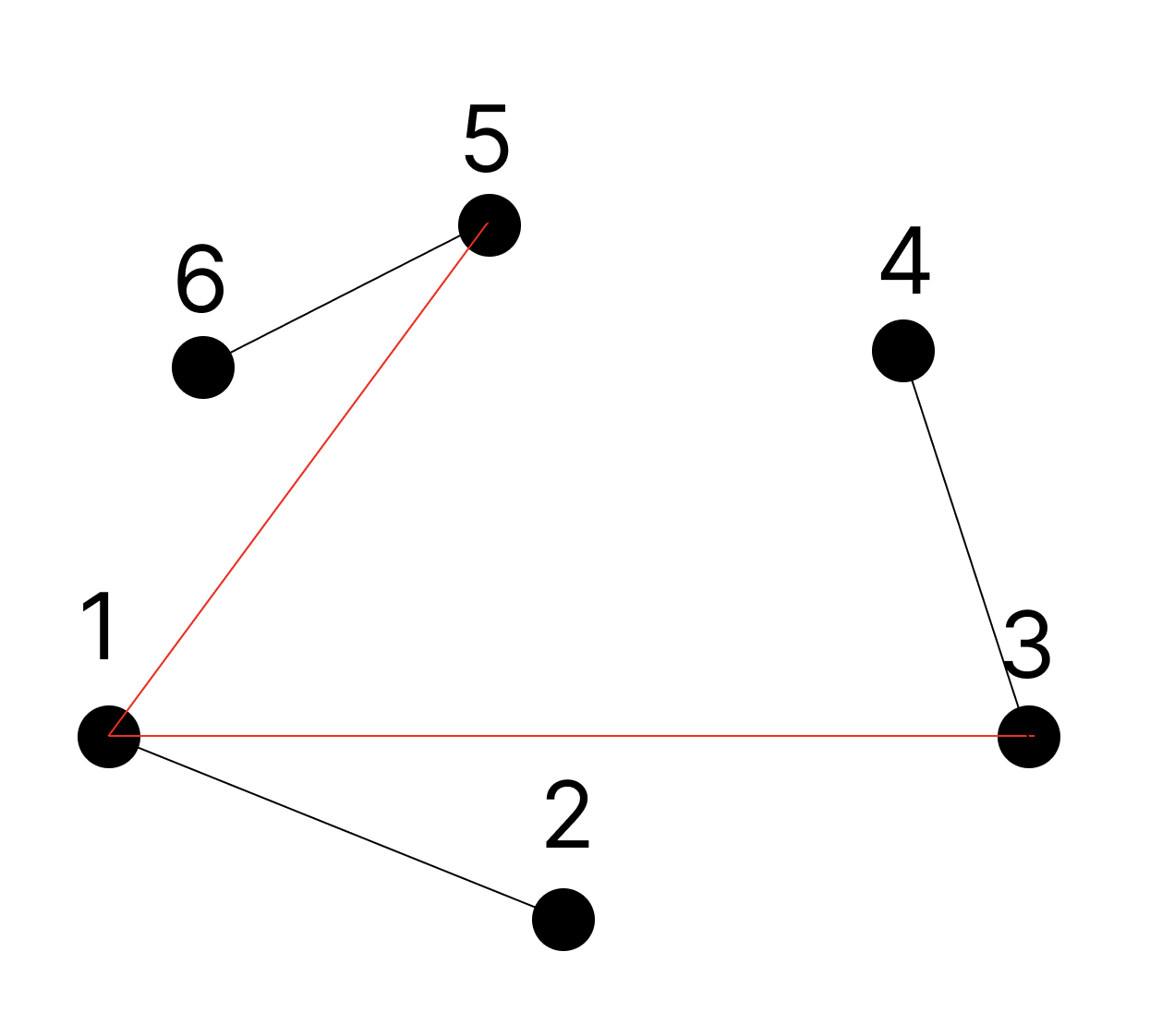
이 그림은 회전하는 캘리퍼스 알고리즘을 가장 정확하게 알려주는 그림이다.
위 그림을 봤을때 무슨 생각이 드는가? 직관적으로 3->4로 갈때는 1에서 멀어지고, 5->6으로 갈때는 1과 가까워 지는 느낌을 받았다면, 필자와 같은 느낌을 받았다고 할 수 있다.

한가지 생각을 더 하기 위하여 다음 그림을 보도록 하자.

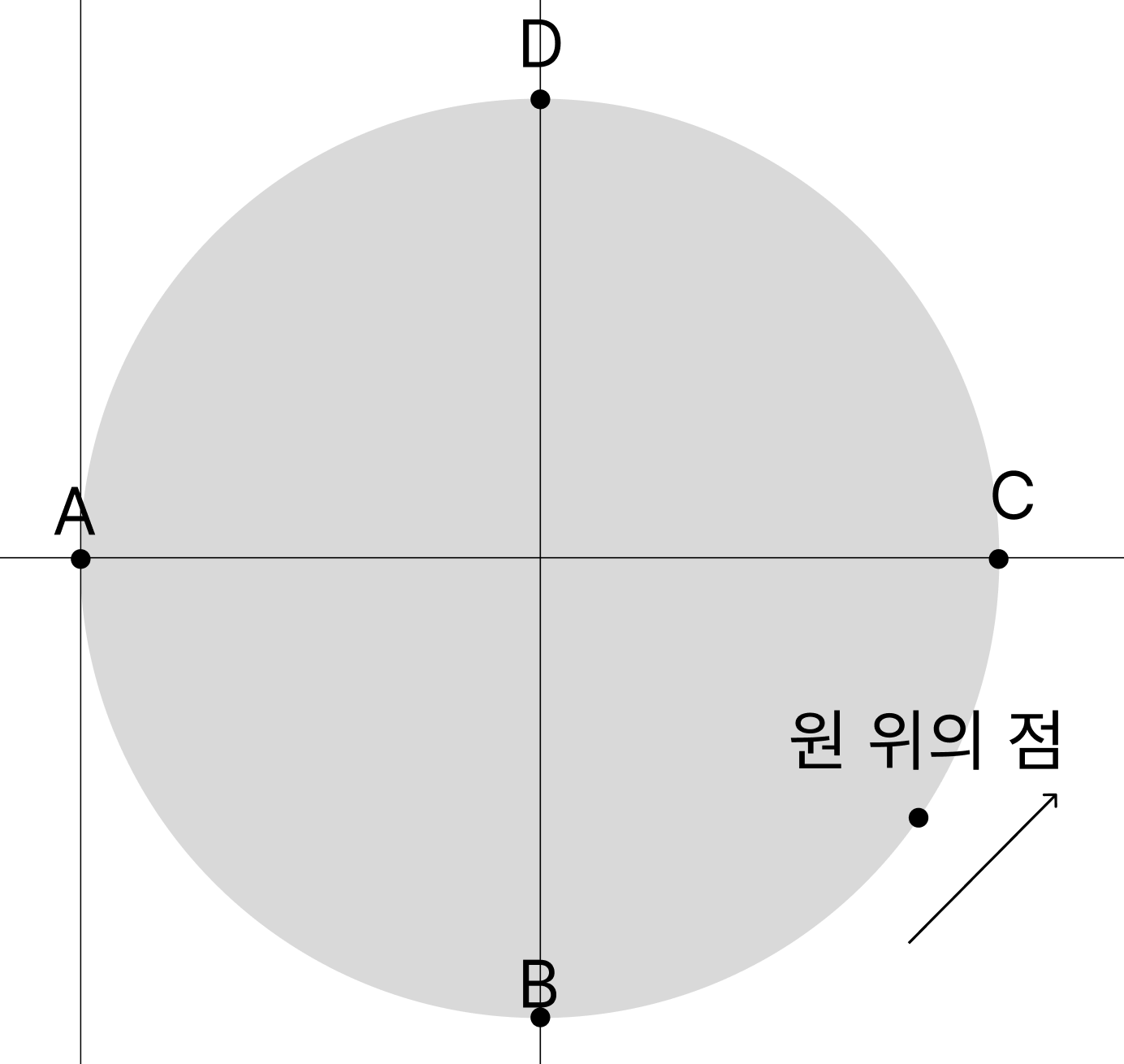
위의 원을 볼때, A -> B -> C 로 갈수록 점과 A의 거리는증가할 것이고,
C -> D -> A 로 갈수록 점과 A의 거리는 줄어들 것이다.

이때, 원과 원위의 점의 접선, 그리고 A와 A의 접선의 CCW를 구하면 다음과 같다.

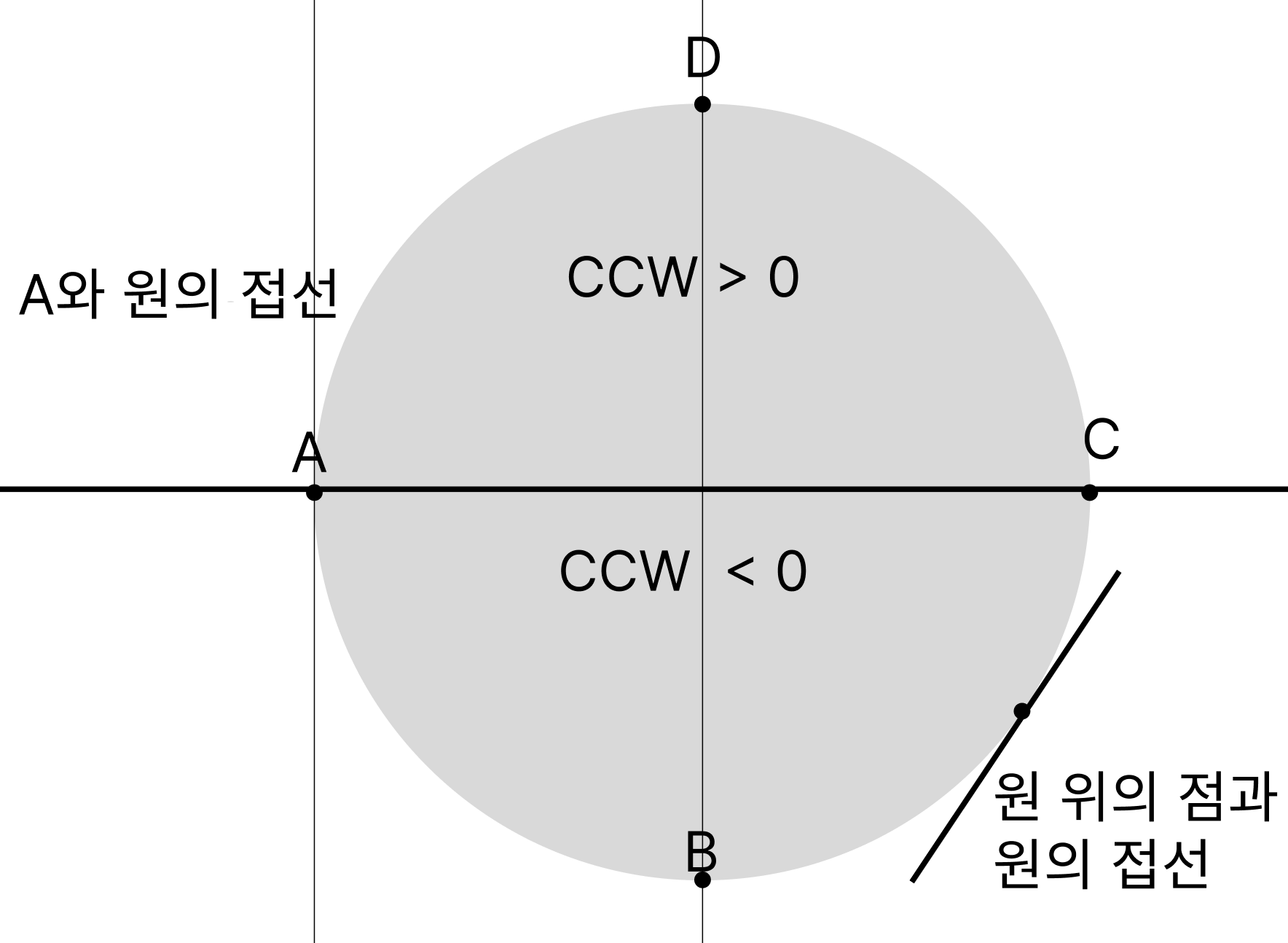
(A 접선은 아래로, 원 위의 점은 반시계방향으로 돈다고 했을때의 계산결과)
위의 계산 결과를 봐도 AC를 기준으로 위, 아래의 CCW가 다르다는 것을 알 수 있다.

자 그럼 결론만 먼저 말한다면, 우리는 CCW < 0인 부분만 계산하면 된다!
왜 그럴까?

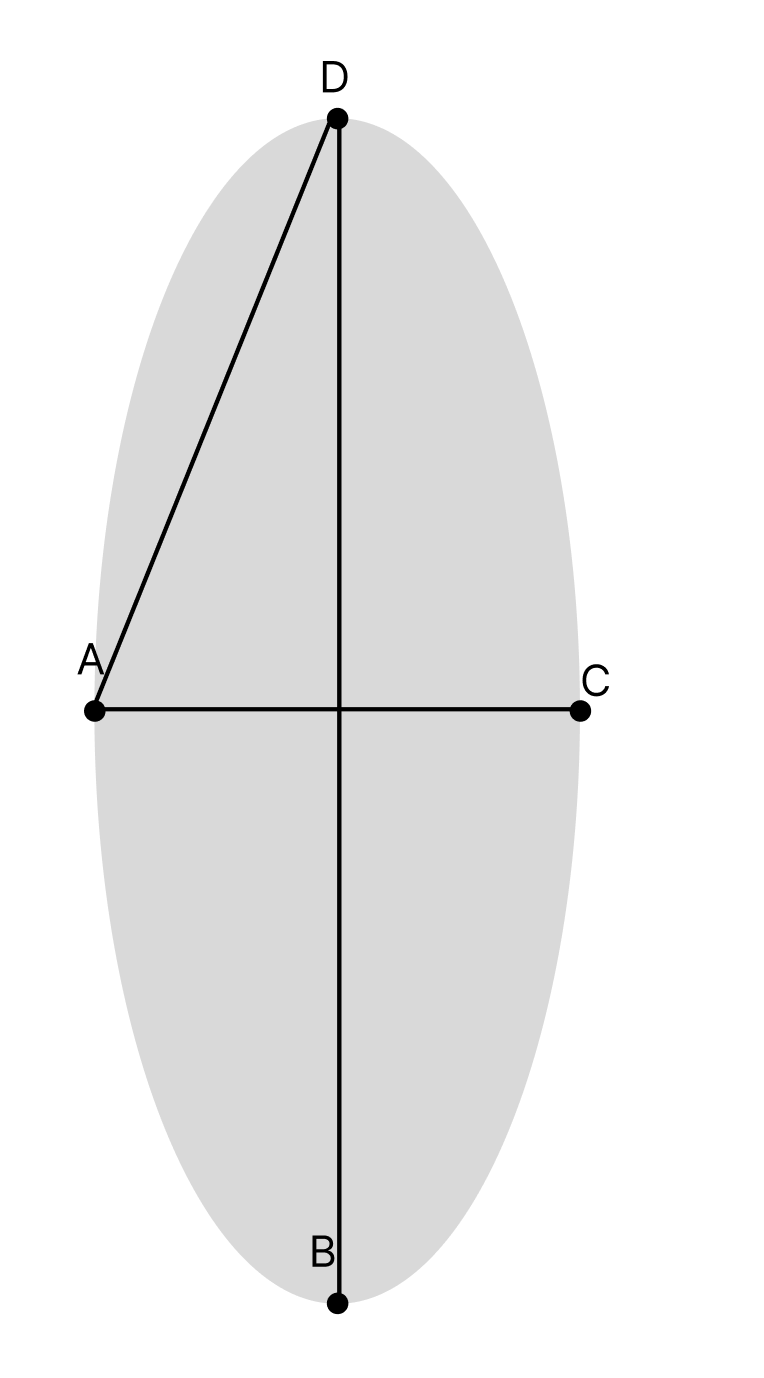
이 말만 들었을때 나오는 가장 간단한 반례는 D가 한참 위로 올라간 타원형일 것이다. 하지만, 우리는 조금 더 생각하면 알 수 있는것이, 그 경우에는 BD 가 가장 긴 선분이 될 것이고, 그것이 최대길이가 될 것이다.

그러니 무슨 말을 하는지 알겠는가?

• 회전하는 캘리퍼스는 한 볼록껍질 집단에서 최대 거리를 가진 두 점을 찾는 알고리즘이다.

• 물론 BD가 길어지는 타원형에서, A에서 CCW < 0인 경우를 찾았을때, B가 최대값이 될 것이고 B보다 D가 더 길어질 수 있다.

• 하지만 그렇다 할지라도, B에서 캘리퍼스 연산을 하였을때 BD의 길이는 AD 길이보다 한참 더 길 것이다.

• 그 이유는, 한 원형 도형에서 가장 긴 선분은 중심을 지나게 될 것이기 때문이다.

라고

필자가 생각해서 정리해 봤다.
수학을 전공하지도, 알고리즘을 잘 알지도 못하기 때문에 틀린점이 있을수 있다.
반례/추가적인 사항은 언제든지 댓글로 알려주시면 감사하겠습니다.

서론이 엄청 길었으니 풀이를 보자.

import sys

def ccw(a,b,c):
    return (a[0]*b[1] + b[0]*c[1] + c[0]*a[1]) - (a[1]*b[0] + b[1]*c[0] + c[1]*a[0])

def cccw(a,b,c,d):
    tmp = d[:]
    tmp[0] -= (c[0] - b[0])
    tmp[1] -= (c[1] - b[1])
    return ccw(a,b,tmp)

def distance(a,b):
    return (a[0]-b[0])**2 + (a[1]-b[1])**2


T = int(sys.stdin.readline())
for i in range(T):
    N = int(sys.stdin.readline())
    city = [list(map(int,sys.stdin.readline().split())) for _ in range(N)]
    city.sort()
    
    
    cal_1 = []
    for i in range(N):
        while len(cal_1) > 1 and ccw(cal_1[-2],cal_1[-1],city[i]) <= 0:
            cal_1.pop()
        cal_1.append(city[i])
            
    cal_2 = []
    for i in range(N-1,-1,-1):
        while len(cal_2) > 1 and ccw(cal_2[-2],cal_2[-1],city[i]) <= 0:
            cal_2.pop()
        cal_2.append(city[i])
    
    cal = cal_1[:-1] + cal_2[:-1]
    num = len(cal)

    MAX = 0
    j = 1
    ans = [[],[]]
    for i in range(num):
        while j+1 != i and cccw(cal[i],cal[(i+1)%num],cal[j%num],cal[(j+1)%num]) > 0:
            if distance(cal[i],cal[j%num]) > MAX:
                ans[0] = cal[i]
                ans[1] = cal[j%N]
                MAX = distance(cal[i],cal[j%num])
            j += 1
        if distance(cal[i],cal[j%num]) > MAX:
                ans[0] = cal[i]
                ans[1] = cal[j%num]
                MAX = distance(cal[i],cal[j%num])
                
    print(*ans[0],*ans[1])

전체 코드이다.
위쪽은 그냥 똑같다.

• 데이터를 sort 하고
• up, down 볼록껍질을 구했다.

이제 할것은 캘리퍼스를 통해서 길이를 구하는 것이다.

    for i in range(num):
        while j+1 != i and cccw(cal[i],cal[(i+1)%num],cal[j%num],cal[(j+1)%num]) > 0:
            if distance(cal[i],cal[j%num]) > MAX:
                ans[0] = cal[i]
                ans[1] = cal[j%N]
                MAX = distance(cal[i],cal[j%num])
            j += 1
        if distance(cal[i],cal[j%num]) > MAX:
                ans[0] = cal[i]
                ans[1] = cal[j%num]
                MAX = distance(cal[i],cal[j%num])
                

이 코드가 캘리퍼스를 구하는 것이다.
CCCW는 뭔가 하겠지만

def cccw(a,b,c,d):
    tmp = d[:]
    tmp[0] -= (c[0] - b[0])
    tmp[1] -= (c[1] - b[1])
    return ccw(a,b,tmp)

단순히 ab / cd 선분을
cd의 c값을 b에 겹치도록 벡터 이동을 한 것 뿐이다.

이 외의 코드를 살펴보면

while j+1 != i and cccw(cal[i],cal[(i+1)%num],cal[j%num],cal[(j+1)%num]) > 0:

while을 통해서 연산을 하는 코드이다.
ccw와 같이 그저 특정 조건일때(ccw > 0) 연산을 한다.

            if distance(cal[i],cal[j%num]) > MAX:
                ans[0] = cal[i]
                ans[1] = cal[j%N]
                MAX = distance(cal[i],cal[j%num])
            j += 1

단지 ccw > 0 이라는 것은 최대값 일 수도 있는 예비 후보이기 때문에 MAX 값과 비교해 가면서 최대값을 구해주고,

        if distance(cal[i],cal[j%num]) > MAX:
                ans[0] = cal[i]
                ans[1] = cal[j%num]
                MAX = distance(cal[i],cal[j%num])

이건 마지막 경계값도 한번 구해주는 것이다.