경로 알고리즘

어느 한 농가를 생각해보자.
이 농가는 엄청 큰 기업농이라 많은 차량이 출입한다.
그리고 농가에서 생산한 농산물을 판매하기 위해서는 주변 상권에 쉽게 접근 가능해야 한다.
이때, 어떤 도로를 통해 이동하면 경제적으로 최대한의 이율을 낼 수있을까?
여기서 관점이 2가지로 나뉜다.
하나는 농가의 주인 시점
다른 하나는 도로까는 사람의 시점(보통 정부)
이때, 도로 경로 계산에 필요한 알고리즘을 생각해 보자.
- 우리집에서 특정 지역까지 갈때 최소비용
- 각 지역에서 다른 지역까지 갈때 최소비용
- 전체 도로의 최소비용
경로 알고리즘을 알아봤던 사람이라면 무슨말인지 대충 기억이 날 것이다.
위를 알고리즘으로 정리해 보면
- 다익스트라 , 벨만-포드, BFS, SPFA
- 플로이드 - 워셜
- 크루스카, 프림 (MST)
이 되겠다.
특징을 적어보자면
점과 점 경로
다익스트라
- 보편적인 경로탐색 알고리즘
벨만-포드
- 음의 경로가 포함되어도 가능함
BFS
- 모든 경로의 가중치가 같을때 사용가능
SPFA
- 벨만-포드의 최적화 버전, 다익스트라와 비슷한 작동방식
각 노드의 경로
플로이드-워셜
- 각 노드별로 다른 노드까지 최소경로를 계산할 수 있음
MST
크루스카
- union - find 기법을 사용하는 알고리즘
- 간선중심, 상황에 따라서 프림한테 밀릴수도 있음
프림
- 우선순위큐를 사용하는 알고리즘
- 정점 중심의 알고리즘
그래서 간선의 개수가 많다면 프림이, 적은 희소그래프라면 크루스카가 유리하다.
코드
다익스트라
import sys
import heapq
V, E = map(int, sys.stdin.readline().split())
N = int(sys.stdin.readline())
graph = [[] for _ in range(V + 1)]
weight = [float('inf') for _ in range(V + 1)]
weight[N] = 0
seq = []
visit = [False for _ in range(V + 1)]
check = V
heapq.heappush(seq, (0, N))
for _ in range(E):
u, v, w = map(int, input().split())
graph[u].append((w, v))
while seq:
dist, node = heapq.heappop(seq)
if visit[node] or weight[node] < dist:
continue
visit[node] = True
check -= 1
for w, v in graph[node]:
if not visit[v]:
if weight[v] > weight[node] + w:
weight[v] = weight[node] + w
heapq.heappush(seq, (weight[v], v))
if check == 0:
break
for i in range(1, V + 1):
if weight[i] == float('inf'):
print("INF")
else:
print(weight[i])
레퍼런스 : 백준 1753 최단경로 풀이
흐름은 다음과 같다.
1. 시작 지점을 정한다.
2. 시작 지점에서 움직일 수 있는 경로를 탐색한다.
3. 그중 이전 경로와 비교해서 더 짧은 경로로 갱신한다.
여기서 중요한건
이전에 추가된 가중치보다 더 작은 값이 들어왔을때
관련된 모든 노드를 재탐색 하여 값을 다시 갱신한다.
오버헤드라고 생각할 수는 있겠지만
한 경로에서 다른 경로까지의 최소 비용을 계산하는 것이기 때문에 어쩔수 없다.
그리고 오버헤드를 줄이기 위한 최적값으로
지금 가진 경로 가중치보다 기존 값이 작다면, continue를 통해 계산을 하지 않는다.
벨만-포드
def bellman_ford(graph, source):
# Step 1: Initialize distances
distances = {vertex: float('inf') for vertex in graph}
distances[source] = 0
# Step 2: Relax edges |V| - 1 times
for _ in range(len(graph) - 1):
for u in graph:
for v, weight in graph[u].items():
if distances[u] != float('inf') and distances[u] + weight < distances[v]:
distances[v] = distances[u] + weight
# Step 3: Check for negative weight cycles
for u in graph:
for v, weight in graph[u].items():
if distances[u] != float('inf') and distances[u] + weight < distances[v]:
raise ValueError("Graph contains negative weight cycle")
return distances
# Example
graph = {
'A': {'B': -1, 'C': 4},
'B': {'C': 3, 'D': 2, 'E': 2},
'C': {},
'D': {'B': 1, 'C': 5},
'E': {'D': -3}
}
source = 'A'
shortest_distances = bellman_ford(graph, source)
print(shortest_distances)
레퍼런스 : https://www.geeksforgeeks.org/bellman-ford-algorithm-in-python/
효율성을 버린 알고리즘이다.
'어떻게 음수 간선도 파악 가능한가?' 라고 한다면
그냥 다 돌려보니까 라고 답할 수 있다.
핵심 코드도 참 간단한데,
# 간선 정보를 이용해 V-1번 반복
for i in range(V - 1):
for u, v, weight in graph:
# 현재 노드 u에서 v로 가는 거리가 더 짧으면 업데이트
if distances[u] != float('inf') and distances[u] + weight < distances[v]:
distances[v] = distances[u] + weight이게 끝이다.
노드수 - 1번 모든 경로를 완전탐색한다.
하나 주의해야 할 부분은
distances[u] != float('inf') 부분이다.
갱신되지 않은 노드에 갱신을 하려고 한다면
-inf + a < distances[v]가 항상 참이 될 것이라 오버헤드가 발생할 것이다.
SPFA
from collections import deque
graph = [[] for _ in range(100000)]
def addEdge(frm, to, weight):
graph[frm].append([to, weight])
def print_distance(d, V):
print("Vertex","\t","Distance from source")
for i in range(1, V + 1):
print(i,"\t",d[i])
def shortestPathFaster(S, V):
d = [10**9]*(V + 1)
inQueue = [False]*(V + 1)
count = [0]*(V + 1)
d[S] = 0
q = deque()
q.append(S)
inQueue[S] = True
while (len(q) > 0):
u = q.popleft()
count[u] += 1
if count[u] > V-1:
print('negative')
inQueue[u] = False
for i in range(len(graph[u])):
v = graph[u][i][0]
weight = graph[u][i][1]
if (d[v] > d[u] + weight):
d[v] = d[u] + weight
if (inQueue[v] == False):
q.append(v)
inQueue[v] = True
# Print the result
print_distance(d, V)
# Driver code
if __name__ == '__main__':
V = 5
S = 1
# Connect vertex a to b with weight w
# addEdge(a, b, w)
addEdge(1, 2, 1)
addEdge(2, 3, 7)
addEdge(2, 4, -2)
addEdge(1, 3, 8)
addEdge(1, 4, 9)
addEdge(3, 4, 3)
addEdge(2, 5, 3)
addEdge(4, 5, -3)
# Calling shortestPathFaster function
shortestPathFaster(S, V)레퍼런스 : https://www.geeksforgeeks.org/shortest-path-faster-algorithm/
(음의 사이클을 찾는 부분이 비어서 추가했음)
Shortest Path Faster Algorithm 이라고 한다.
위의 벨만-포드와의 차이점이라고 한다면
Que와 inQueue를 활용해서 연산을 관리한다.
여기서 좀 놀랐는데, 왜 Que에 넣을때 inQueue[v] = True를 할까?
그 답은 이미 Que에 들어가 있는 노드는 중복해서 연산하지 않는다는 것이다.
또한 연산을 해서 Que에서 빠졌음으로, 재연산이 가능하게 만든다는 것이다.
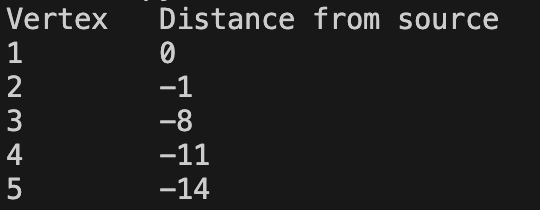
또한, 각 노드를 갱신하는 횟수가 V-1보다 많다면 음의 간선이 발생해서 계속 갱신하는것이라 판단할 수 있다.
그리고 생각보다 엄청 빠르다고 한다.
플로이드 워셜
# Floyd-Warshall 알고리즘 구현
def floyd_warshall(graph, V):
# 최단 거리 배열을 초기화
dist = [[float('inf')] * V for _ in range(V)]
# 자기 자신으로의 거리는 0으로 초기화
for i in range(V):
dist[i][i] = 0
# 간선의 가중치로 초기화
for u in range(V):
for v, weight in graph[u]:
dist[u][v] = weight
# 플로이드-워셜 알고리즘 수행
for k in range(V):
for i in range(V):
for j in range(V):
if dist[i][j] > dist[i][k] + dist[k][j]:
dist[i][j] = dist[i][k] + dist[k][j]
return dist
# 그래프 표현: 인접 리스트
# graph[u] = (v, weight) : u에서 v로 가는 가중치 weight
graph = [
[(1, 2), (2, 5)], # 0번 노드에서 1번 노드로 가는 가중치 2, 2번 노드로 가는 가중치 5
[(2, 3)], # 1번 노드에서 2번 노드로 가는 가중치 3
[(3, 5)], # 2번 노드에서 3번 노드로 가는 가중치 -4 (음수 간선)
[(1, 6)] # 3번 노드에서 1번 노드로 가는 가중치 -2 (음수 간선)
]
# 노드의 개수
V = 4
# 모든 노드 쌍 간의 최단 경로 계산
distances = floyd_warshall(graph, V)
# 결과 출력
print("최단 거리 행렬:")
for row in distances:
print(row)
모든 간선을 확인하고 싶다 = 브루트 포스 실행
for k in range(V):
for i in range(V):
for j in range(V):
if dist[i][j] > dist[i][k] + dist[k][j]:
dist[i][j] = dist[i][k] + dist[k][j]
핵심 코드도 간단하다.
다 계산하면 된다.
크루스카
# 유니온-파인드(Union-Find) 자료 구조 구현
class UnionFind:
def __init__(self, n):
self.parent = list(range(n)) # 각 노드는 자기 자신을 부모로 초기화
self.rank = [0] * n # 트리의 높이(랭크) 저장
def find(self, u):
if self.parent[u] != u:
self.parent[u] = self.find(self.parent[u]) # 경로 압축
return self.parent[u]
def union(self, u, v):
root_u = self.find(u)
root_v = self.find(v)
if root_u != root_v:
# 트리의 높이가 낮은 쪽을 높은 쪽에 붙인다 (랭크에 따라 union)
if self.rank[root_u] > self.rank[root_v]:
self.parent[root_v] = root_u
elif self.rank[root_u] < self.rank[root_v]:
self.parent[root_u] = root_v
else:
self.parent[root_v] = root_u
self.rank[root_u] += 1
# 크루스칼 알고리즘 구현
def kruskal(graph, V):
# 결과 저장 (MST에 포함된 간선)
mst = []
# 간선을 가중치 기준으로 정렬
edges = sorted(graph, key=lambda x: x[2])
# 유니온-파인드 자료 구조 초기화
uf = UnionFind(V)
# 간선들을 순회하면서 MST 구성
for u, v, weight in edges:
# u와 v가 같은 트리에 속해 있지 않으면, 간선을 추가하고 union
if uf.find(u) != uf.find(v):
uf.union(u, v)
mst.append((u, v, weight))
return mst
# 그래프 표현: (출발 노드, 도착 노드, 가중치) 형태로 간선 정보 저장
graph = [
(0, 1, 2), # 0번 노드에서 1번 노드로 가는 가중치 2
(0, 3, 6), # 0번 노드에서 3번 노드로 가는 가중치 6
(1, 3, 8), # 1번 노드에서 3번 노드로 가는 가중치 8
(1, 2, 3), # 1번 노드에서 2번 노드로 가는 가중치 3
(2, 3, 5), # 2번 노드에서 3번 노드로 가는 가중치 5
(2, 4, 7), # 2번 노드에서 4번 노드로 가는 가중치 7
(3, 4, 9) # 3번 노드에서 4번 노드로 가는 가중치 9
]
# 노드의 개수
V = 5
# 크루스칼 알고리즘을 사용하여 최소 신장 트리를 구합니다.
mst = kruskal(graph, V)
# 결과 출력
print("최소 신장 트리의 간선들:")
for u, v, weight in mst:
print(f"({u}, {v}) - 가중치: {weight}")
흐름을 살펴보자면
- 함수를 초기화한다.
- 간선들을 순회한다.
- 이때 둘이 같은 트리에 있지 않으면, union을 통해 merge한다.
왜 되는가 싶겠지만
간선을 기준으로 sort() 해버렸기 때문에
먼저 나온 간선부터 확인해서 append 해도 MST가 완성된다.
이때, 위의 코드에서는 union을 할때 경로압축을 철저하게 했지만,
단순하게 해도 시간복잡도가 정말 많이 줄어든다.
def find(parent, x):
if parent[x] != x:
parent[x] = find(parent , parent[x])
return parent[x]
def union(parent , start , end):
A = find(parent , start)
B = find(parent , end)
if(A != B):
parent[A] = B
이렇게만 해도 충분하다 왠만하면..
대회나갈꺼면 rank까지 해야겠지만
rank 최적화 안해서 떨어질 시험은 애초에 공부 해서 나가야된다..
프림
import heapq
def prim(graph, V):
# MST에 포함된 노드들
visited = [False] * V
# 우선순위 큐: (가중치, 시작 노드, 끝 노드) 형태로 간선 저장
min_heap = [(0, 0)] # 시작 노드는 0번, 가중치는 0으로 초기화
mst_cost = 0
mst_edges = []
while min_heap:
weight, u = heapq.heappop(min_heap)
# 이미 방문한 노드는 무시
if visited[u]:
continue
# 노드를 MST에 추가
visited[u] = True
mst_cost += weight
# 현재 노드와 연결된 간선들을 우선순위 큐에 추가
for v, w in graph[u]:
if not visited[v]:
heapq.heappush(min_heap, (w, v))
return mst_cost
# 그래프 표현: 인접 리스트
graph = [
[(1, 2), (3, 6)], # 0번 노드에서 1번 노드로 가는 가중치 2, 3번 노드로 가는 가중치 6
[(0, 2), (2, 3), (3, 8)], # 1번 노드에서 연결된 노드들
[(1, 3), (3, 5), (4, 7)], # 2번 노드에서 연결된 노드들
[(0, 6), (1, 8), (2, 5), (4, 9)], # 3번 노드에서 연결된 노드들
[(2, 7), (3, 9)] # 4번 노드에서 연결된 노드들
]
# 노드의 개수
V = 5
# 프림 알고리즘을 사용하여 최소 신장 트리를 구합니다.
mst_cost = prim(graph, V)
# 결과 출력
print(f"최소 신장 트리의 비용: {mst_cost}")
크루스카는 1차원 리스트 형식으로, 프림은 BFS형식으로 푼 문제이다.
하지만 중요한 것은 간선의 가중치를 heapq를 기준으로 넣을때마다 최적화 시켜야한다는 것이다.
간선의 개수가 많아질수록 프림이 유리한 이유는
각 노드별로 BFS를 실시하기 때문에 가중치는 작지만 갱신시키지 못하는 간선들을 생략하고 계산에 필요한 간선들을 우선적으로 계산할 수 있다는 장점이 있다.

