이번 글은 '코딩테스트'를 중점으로 정리를 할 계획이다.
하지만 많이 적을건 아니고, 이런 개념은 알았으면 한다는 것으로 이해해주면 된다.
글 쓰는 주인장 주관이 100프로 들어가있기 때문에 '이렇게 하는 사람도 있구나' 느낌으로 보면 된다.
그리고 알고리즘 쪽은 안풀어본사람이 이해 못할수 있음.
문제 풀이 전략
- 일단 푸는거를 목표로 한다.
- 풀었으면 시간을 줄일 수 있는지 확인한다.(이진탐색, 오버헤드 제거 등등)
- 안되면 포기하고 딴거로 넘어간다.
- 빠르게 한번 훑고, 뒤에도 안되면 그냥 앞에꺼부터 시간 쓴다.
라이브러리
기본 함수
import sys
a = int(input()) # 기본 입력
b = int(sys.stdin.readline()) # sys 입력
c, d = map(int,input().split()) # 띄어쓰기 입력
# input data = '1 2' / c = 1, d = 2
e = list(map(int,input().split())) #띄어쓰기 리스트
# input data = '1 2 3 4 5', e = [1,2,3,4,5]
f = str(input().strtip()) # 문자열 공백 제거
# input data = ' 123 ' . f = '123'
data = [3,5,6,2,1,4]
data.sort() // data = [1,2,3,4,5,6] 정렬기능
cal = sorted(data) # cal = [1,2,3,4,5,6] 정렬한 데이터를 가져옴
min(data) # 최소값, 1
max(data) # 최대값, 6
sum(data) # 리스트 합, 21
String = [c,o,d,i,n,g, ,t,e,s,t]
''.join(String) # 'coding test' , 문자열 합치기
data = "}replacetest"
data = data.replace('}', '') # 특정 데이터 치환
print(data) # replacetest
안쓰는거
eval -> 쓰지마세요 너무나도 위험한 함수이고, 코테에서는 쓸일도 없습니다.
복사에 관해
a = [1]
b = a
a[0] += 1
print(b)이거 값 2나온다.
a = 1
b = a
a += 1
print(b)이건 1나온다.
list는 linked 자료형이기 때문에 같은 데이터를 2개의 리스트가 가리키고 있는것에 불과하다.
a = [1]
b = a.copy()
a[0] += 1
print(b) # [1]
a = [1]
b = a[:]
a[0] += 1
print(b) # [1]
그러니까 깊은 복사를 하던, 슬라이싱을 하던 참조가 아닌 새로운 리스트를 만들어야 한다.
근데 파이썬 쓰다보면 list 복사는 잘 안하게 된다.
itertools
import itertools
arr = ['A', 'B', 'C']
nPr = itertools.permutations(arr,2)
nCr = itertools.combinations(arr,2)각각 순열, 조합이 나온다.

순열은 '중복을 허용한 모든 경우'
조합은 '중복이 불가능한 모든 경우'
라고 생각하면 된다.
근데 하나 골때린거는 리턴값이 튜플값으로 튀어나오기 때문에 list연산하면 오류가 난다.
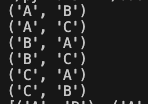
for i in nPr:
print(list(i))
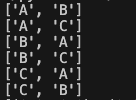
그래서 데이터를 가지고 뭘 할려면 그대로 사용하거나, list로 바꾼다음에 써야 한다.
heapq
2개만 외우자.
import heapq
lst = []
heapq.heappush(lst, A) # A를 heap으로 lst에 추가
heapq.heappop(lst) # lst에서 heappop 하나 함.
간단하지만 강력한 테크닉
위에서 heapq를 사용하면 '작은 숫자부터' 꺼낸다.
import heapq
lst = []
heapq.heappush(lst, -A) # A를 음수로 lst에 추가
heapq.heappop(lst) # lst에서 heappop 하나 함. 이때 음수가 붙은 A가 큰순서대로 나옴
위 처럼 음수로 만든다음에 함수에 집어넣으면 절대값이 커질수록 작은 수가 되기 때문에,
큰수부터 튀어나오게 된다.
그러니까, 넣을때 음수 붙여서 넣고, 뺀 다음 음수 때버리면 큰수부터 나오는 heap을 만들 수 있다.
간단한데 이거 알고 모르고는 풀수있고 없고 차이다.
bisect
binary search 기반이라서 무진장 빠르다.
import bisect
# case 1
lst = [1,2,3,4,5,6,7,8,9]
print(bisect.bisect_left(lst,2)) # 특정값의 왼쪽 인덱스, 1
print(bisect.bisect_right(lst,2)) # 특정값의 오른쪽 인덱스, 2
print(lst[1:2]) # [2]
# case 2
lst = [1,3,5,7,9]
print(bisect.bisect_left(lst,4)) # 2
print(bisect.bisect_right(lst,4)) # 2
print(lst[2:2]) # []
# case 3
lst = [1,3,5,7,9]
print(bisect.bisect_left(lst,3)) # 1
print(bisect.bisect_right(lst,8)) # 4
print(lst[1:4]) # [3,5,7]
왜 햇깔리게 리스트에 있는수를 적었냐?
그래야 재대로 이해가 되기 때문이다.
case1을 보면 bisect 계산의 범위로 list를 짜르니 정상값이 나온다.
case2은 bisect 계산 범위로 짜르면 []값이 나온다.
case3은 [3,5,7]이 나오는걸 알 수 있다.
그러니까, bisect로 짤랐을때 값이 어떻게 나올지 예상해보면 쉽게 이해할 수 있다.
collections
import collections
lst = collections.Counter(['a','b','a','a','c','b'])
print(dict(lst)) # {'a': 3, 'b': 2, 'c': 1}솔직히 이번에 정리하면서 처음 본 함수이다.
Counter로 dict 자료형을 뱉는다.
이거 다른 연산나오면 그냥 죽어라는 소리니까 딴거나 열심히 풀자.
import collections
lst = collections.deque()
lst.append(3)
lst.popleft()
print(lst)deque다. 위의 3개만 알아놔도 잘 써먹는다.
math
솔직하게 말하면 나는 math를 거의 안쓴다.
수학 문제를 많이 풀지도 않아서 그렇다.
조금만 외워도 유용하지만 쓸 상황이 나올까?
개인적으로는 math 연산이 필요한 상황이 나오면 그 코테는 변별력이 없다고 본다.
특정 라이브러리를 알고 모르고 차이가 너무 심하다.
하지만 몇몇을 정리해 보겠다.
import math
math.gcd(121,154) # 11, 최대공약수
math.sqrt(3) # 제곱근
# 내림, 올림
math.floor(12.345) # 12
math.ceil(12.345) # 13이 외에도 자연상수니, pi니 있는데 안쓸거고
저 gcd가 유클리드 호제법 기반이라 엄청 빠르다.
괜히 최대공약수 구할려고 하지말고 math.gcd 쓰자. 저거보다 빠른거 만드는건 현실적으로 힘들다.
자료구조
알아야 할 내용
코테칠때 필요한 지식을 적음.
- 스택
- 큐
- 힙큐
- 리스트
- 해시
- 그래프
- 트리
stack, queue, heapq
stack = .append(), .pop() 사용. LIFO
queue = .append(), popleft() 사용. FIFO
heapq = 데이터를 오름차순/내림차순으로 빠르게 관리하는거
List
a = list(map(int,input(),split()))위의 형태를 많이 가짐.
특정값을 저장하고 가공하기 매우 편함.
hash
쉽게 말하면 전화번호부 같은거
특정 값을 Key로 Value를 찾기 쉽게 만듬.
해시 작성
lst = [1,2,3,4,5]
hash = {}
for i in lst:
if i in hash:
hash[i] += 1
else:
hash[i] = 1
print(hash)
print(hash[1] + hash[3]) # 1+1 = 2
hash['text'] = 'coding'
print(hash['text']) # 'coding'
for i in hash:
print(hash[i])
해시에 값을 집어넣는건 가능하다.
.append()를 쓰는게 아니라, hash[key] = value 모양으로 집어넣으면 된다.
그리고 Key값에 맞게 데이터를 가져올 수 있고, Key, Value 둘다 str 자료형이 된다.
중복값 제거
lst = [1, 2, 2, 3, 4, 4, 5]
dup = set(lst) # 중복 제거
print(dup) # {1, 2, 3, 4, 5}중복된 데이터를 쉽게 제거할 수 있다.
위의 2개만 알아도 코테에서 정말 유용하게 쓸 수 있다.
하지만 중요한 점은, set은 dict와 달리 Value값이 없다.
해시로 사용할려면 set으로 리스트를 변환하지 말고, {}를 통해서 직접 집어넣자.
그래프 vs 트리
트리 상위개념이 그래프
트리는 루트 노드 하나 가지고 하위 노드가 달린거
그래프는 노드끼리 연결된거
그래프가 트리를 포함하는 개념임
튜플?
일단 나는 튜플 안쓴다.
어차피 list로 변형해서 쓸 수도 있고, permutation/combination에서 나온 튜플들도 값만 빼와서 쓸 수 있다.
튜플은 순서를 따르는 데이터라는 점이 중요하다.( [1,2] != [2,1])
그러니 tuple()에 잡히지 말고, list형태로 바꿔서 풀 수도 있다.
중요한건 순서다.
알고리즘
진짜 간단하게 훑고 지나갈거다.
그리디
순서대로 계산하다가 걸리면 return 하면된다.
그리디는 직관적으로 풀어야 하기 때문에 감만 잘 잡으면 된다.
브루트 포스
각 잘보자. 괜히 DP같은 문제 브루트 돌려도 답 나오게 자료줄 수 있음.
DFS/BFS
DFS는 루트에서 하나를 깊게 들어간다는 느낌.
def DFS():
# 알고리즘 로직
DFS()이러한 형식을 가지고 있다.
추가적으로 백트래킹은 공부좀 해야 한다.
def DFS():
# 알고리즘 로직
count += 1
DFS()
count -= 1뭐 이런 느낌이다.
하지만 BFS는 루트에서 하위 노드들을 전부 훑는다는 느낌.
que = deque()
def BFS(A):
# 로직을 위한 셋팅
for i in range(N):
# 로직
if ~~~:
que.append(i)
대략 이런 모양을 가지고 있다.
공통점이라면 Visited와 같은 중복 check 기능이 들어갈 수 있다는것.
코드 짤때 팁은
모든 과정을 다 집어넣으려고 하지 말고
가장 작은 단위가 되는 부분을 구현하려고 해라
어차피 모듈 반복연산이다.
DP
탑다운/바텀업 방식이 있다.
설명을 위해 내가 자주 예시를 드는 fibo를 사용하겠다.
탑다운은 memoization을 쓴다.
def fibo(n):
return fibo(n-1) + fibo(n-2)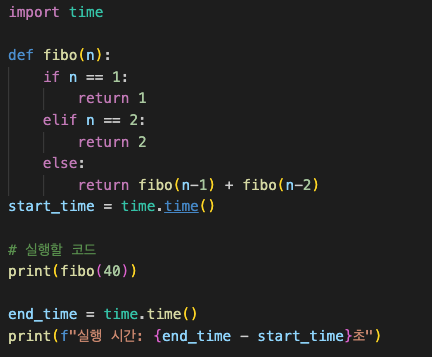

탑다운은 구현이 간단하다. 대신에 컴퓨터가 혹사한다.
fibo 40 넣었는데 7초나 걸린다.
n에 10000 정도 넣으면 cpu가 뜨끈해지는걸 느낄 수 있다.
적은 자료를 가지고 구현하는 것이라면 복잡하게 바텀업 하겠다고 시간쓰는것보다
탑다운으로 빨리 구현하고 넘어가는것도 하나의 좋은 선택지가 될 수 있다.
하지만 위에서 봤듯이 잘못걸렸다가는 컴퓨터가 작살난다.
바텀업은 tabulation을 사용한다.
def fibo(n):
lst = [0]*(n+5)
# 대충 짤때 패딩 한두개 넣어도 아무 문제 없음.
# 특히나 이런 문제에서는 n에 패딩 좀 넣은걸로 if문을 줄여 깔끔한 코드를 작성할 수 있음.
lst[1] = 1
lst[2] = 1
if n > 2:
for i in range(3,n+1):
lst[i] = lst[i-1] + lst[i-2]
return lst[n]
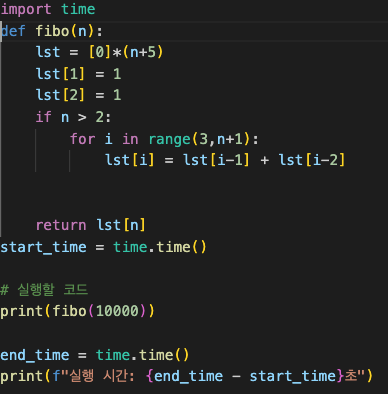

단 0.002초만에 fibo(10000) 연산이 가능한 모습을 보인다.
이처럼 바텀업 방식은 끝내주는 성능을 보여주지만, 상대적으로 구현하기 어렵다는 단점이 있다.
이분탐색
포인터 2개 잡고 반나누기 반나누기 하면 된다.
- left, right 잡고
- middle = (left + rignt) // 2 값 잡는다.
- 이때 middle 값이 원하는 값 보다 크다면, middle이 작아져야 하니 middle = right 한다.
- 원하는 값보다 작다면, middle이 커져야 하니 middle = left 된다.
- 위 과정을 while 통해서 계속 빙글빙글 돌리면 된다.
기타
여기에서는 안적을껀데 해볼만한거 적어봄.
- 다익스트라
- 플로이드 와샬
- 프림
- lcs
- lis
- 비트마스킹
- KMP
- 트라이
- 트리에서 가장 멀리 떨어진 노드
이런게 있는데
솔직히 생각해서 저런게 나올까? 라는 생각을 한다.
다익스트라의 경우는 나온다는 말이 종종 있고, 실제로 카카오 코테에서 다익스트라 문제가 나왔다.
하지만 다익스트라 - 플로이드 워셜 - 프림 - 유니온파인드(+경로압축) - 벨만/포드 등등
전부 경로 탐색 과정에서 나오는거라 하나만 이해해도 나머지는 다 되는 수준이긴 하다.
진짜 문제는 다음과 같다.
1. KMP, Trie 같은 문제는 기본이 백준 기준으로 골드 상위 ~ 플래권이다.
2. 이런거 공부할사람들은 내 블로그 안읽는다.
그러니 내가 말하고 싶은건 다음과 같다.
일단 기본적인 알고리즘부터 빡세게 공부한 다음에 위의 문제를 준비하자.
물론 다 알고 준비하면 좋긴 하겠지만, 우리의 시간은 한정적이다.
잡기술 몇개
.append

시간 체크할때 쓰는 timer 함수이다.
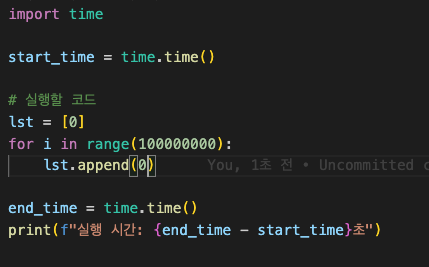

.append를 사용할때 = 3.287초
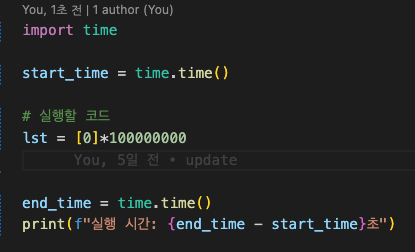

그냥 *사용해서 만들때 = 0.139초
.append는 부득이할때나 쓰는거지
시간잡아먹는 괴물이다.
절때 함부로 사용하지말자.
in
자료가 무식하게 많을때 in을 사용하는게 시간낭비가 될 수 있음.
import time
import bisect
start_time = time.time()
# 실행할 코드
lst = [0]*100000000
for i in range(100000000):
lst[i] = i
if 99999999 in lst:
print('yes')
# 실행 시간: 4.4952287673950195초
print(bisect.bisect_left(lst,99999999 ))
# 실행 시간: 5.383937120437622초
end_time = time.time()
print(f"실행 시간: {end_time - start_time}초")
위의 경우를 보면 1억번 해서 1초 늦어진건데 뭔 호들갑이냐 라고 할 수 있지만
5.3초와 4.5초는 약 20퍼 차이다.
logn과 n의 차이는 생각보다 크다.
정렬되고, 특정값을 뽑는 경우라면 이진탐색을 고려하자.
2중 for문
대놓고 풀지말라는게 있다.
특히 코테에서 함정 파놓고 2중 for문으로 간단하게 풀리는 문제가 있을수 있는데,
이때는 DP가 아닌지, 다른 방법은 없는지 항상 고민하자.
캐시 히트율
약간 어이가 없을 것이다.
import time
start_time = time.time()
# 실행할 코드
lst = [[0]*10000] * 10000
for i in range(10000):
for j in range(10000):
lst[i][j] = i
#실행 시간: 5.185602188110352초
for j in range(10000):
for i in range(10000):
lst[i][j] = i
#실행 시간: 4.775227069854736초
end_time = time.time()
print(f"실행 시간: {end_time - start_time}초")위의 실행은 아래쪽이 약 10프로 빠르다.
왜 사람들이 관습적으로 2중 포문을 lst[i][j]로 쓰는지 고민 해 봤는가?
재귀 호출 깊이 제한
import sys
sys.setrecursionlimit(100000)이거 limit 숫자 높히면 스택 크기 커져서 메모리 잡아먹는다. 적절하게 사용하자
해시 사용
import time
import bisect
start_time = time.time()
lst = [i for i in range(100000000)]
if 999999999 in lst: # O(n)
print("Found")
# 실행 시간: 1.2391316890716553초
s = set(lst)
if 500 in s: # O(1)
print("Found")
# 실행 시간: 5.158193826675415초
end_time = time.time()
print(f"실행 시간: {end_time - start_time}초")
위를 각각 실행시켜보면 set이 훨씬 느리다.
import time
import bisect
lst = [i for i in range(100000000)]
s = set(lst)
start_time = time.time()
if 500 in s: # O(1)
print("Found")
# 실행 시간: 0.000141143798828125초
end_time = time.time()
print(f"실행 시간: {end_time - start_time}초")
하지만 위와 같이 바꾸면 0.0001초만에 연산을 끝낸다.
Hash로 전환하는데 비용이 발생했지만, 이후 검색할때 O(1)이 되기 때문에
비교할 수 없이 빠르다.
len()
이거 작동시간 O(1)이다.
내적으로 카운터가 있다고 한다.
그러니까 자료형 길어졌다고 변수 하나 지정해서 쓰다가 시간 늘려먹지말고
편하게 len() 쓰면 된다.

