(코테를 처음 봤는데 내 자신을 되돌아보게 되었다..)

청사진이라는 아키텍처 또는 공학 설계를 문서화한 기술 도면을 인화로 복사하거나 복사한 도면을 의미한다.

알고리즘을 처음 배운 사람들은 알고리즘을 이해하기에 바빠서 어떻게 적용시키는가에 많은 고민을 하게 되는데 , 막연하게 적용시킬려는게 아닌 , 알고리즘을 도면화 시켜서 대입을 하면 된다.

그러니까 문제를 봤을때 , 이건 어떤 알고리즘으로 풀어야 하는가? 를 고민하는 것이 아닌 , BFS로 풀때 , DFS로 풀때 , TRI로 풀때 등등 여러가지를 대입하면서 견적을 짜는것이다. 이 과정이 숙달이 되면 문제를 봤을때 어떤 알고리즘은 어느정도 시간이 걸리고 , 어떤 알고리즘은 구현이 너무 힘들고 하는 대략적인 사이즈가 나온다.

이러한 과정이 반복숙달되면 문제풀이 속도는 비약적으로 상승하게 된다.

알고리즘을 풀때도 정규화가 필요하다.

Introduction

기본적으로 코드는 '대충' 적을 것이다.
성의없이 적는 것이 아닌 , 알고리즘의 흐름을 이해하는 것이 중요하다는 것이며 , 세세한 디테일은 본인이 직접 알고리즘 문제를 풀면서 확인하도록 하자.

하지만 바로 밑에 나오는 거듭제곱과 같이 디테일 자체가 중요한 코드들은 자세하게 적을 예정이다.

무엇보다도 이 글에서 가장 중요한 것은 알고리즘을 풀때 어떠한 흐름으로 진행되는가를 이해하는 것이고 , 밑에 나오는 흐름들은 코테 치기전에 '필수'로 이해하고 손코딩 할 줄 알아야 한다.

즉 , 아래에 나오는 코드들은 어떠한 도움도 받지않고 스스로 구현할 수 있어야 한다는 뜻이다.

++ 필자는 python을 주력으로 사용해 알고리즘을 풀기 때문에 python으로만 작성한다.
++ 흐름만 신경쓰면서 적었기 때문에 수도코드를 보면 문법에 안맞거나 디테일이 깨지는 코드가 다수 있을것이다.

거듭제곱

이 코드는 복잡한 방법으로 쓰여진 코드입니다. 2진수로 치환하지 않더라도 곱해야 하는 수를 2로 나누며 0이나올때 pass , 1이나올때 곱하는 방식으로 풀어도 같은 값이 나옵니다.

def matrix(a:list,b:list,n:int): # 행렬곱
    c = []
    for i in range(n):
        row = []
        for j in range(n):
            result = 0
            for k in range(n):
                result += a[i][k] * b[k][j]
            row.append(result)
        c.append(row)
    return c

while True :     #B를 2진수로 치환
    t = B%2
    if t == 1:
        B = (B-1)//2 
    else: B = B//2
    binary.append(t)
    if B <= 1:
        binary.append(B)
        break


for i in range(len(binary)): #2진수로 바꾼 binary를 이용해서 계산
    if binary[i] == 1:
        answer = matrix(answer,in_matrix,N)
        answer = [[x % 1000 for x in row] for row in answer]
    in_matrix = matrix(in_matrix,in_matrix,N)
    in_matrix = [[x % 1000 for x in row] for row in in_matrix]

10830 행렬 제곱의 코드 일부를 가져온 것이다.
가끔가다보면 어떤 숫자의 10만번 1억번씩 곱하라는 문제들이 나오는데 , 이거 전부다 제곱을 사용하면 편하게 나온다.

제곱을 할때의 연산량은 엄청 낮다.
65536번 곱하는것도 한 4번정도 제곱하면 나온다.

위의 코드를 보자.

• 곱해야 하는 횟수를 2진수로 나타낸다.

• 행렬을 제곱하다가 2진수에 맞게 곱해준다.

2줄만에 풀리긴 하지만 처음 보는 사람들은 뭔가 이해가 잘 안될것이다.
왜냐하면 거듭제곱과 2진수가 잘 생각이 되지 않기 때문이다.

다음 2진수를 보자.

1 1 1 1 1 1

이 수를 10진수로 바꿀려면 어떻게 해야할까?
정답은 바로 2^(각 자릿수)를 한 후 더하면 된다.

2^(5) + 2^(4) + 2^(3) + 2^(2) + 2^(1) + 2^(0)

계산값은 63이 된다.

그럼 이제 13번 곱해야 하는 수의 계산량을 2진수로 바꿔보자.(랜덤한 수를 정한거고 아무 의미없음)

2^(3) + 2^(2) + 0*2(1) + 2^(0)

즉 우리는 큰 수를 곱할때 제곱수를 계산하고 있다가 2진수에 맞춰서 곱해주면 되는 것이다.

BFS

from collections import deque()
dx = [1 , -1 , 0 , 0]
dy = [0 , 0 , 1 , -1]

def BFS (lst):
	while lst:
	a , b = lst.popleft()
    for k in range(4)
    x = a + dx[k]
    y = b + dy[k]
    if 0<= x < N and 0 <= y < M and ~~~:
        // 추가조건~~
        lst.append([x , y])
    return count

lst = deque(input())
table = []
print(BFS(lst))

위 코드는 2차원 테이블에서 상하좌우로 움직일 수 있을때 , 특정 조건을 만족하기 위해서 몇 턴이 지나야 하는지를 찾는 수도코드 이다.

• input()으로 lst와 table의 값을 입력받는다. 이때 lst는 deque 선언이다.

• while lst로 lst의 내용이 없을때 반복을 끝낸다.

• x , y 좌표를 받아낸 후 , if문을 돌려서 조건에 맞는 좌표를 추가한다. 이때 table의 값을 변경하거나 count를 세거나 상황에 맞게 추가조건을 정해주면 된다.

• 이후 값은 return 으로 받아내거나 , 함수를 쓰지 않고 특정 리스트에 값을 저장하는 방식으로 해도 되고 여러가지 방법 중 하나를 사용해 원하는 답을 얻어낸다.

DFS(재귀)

def DFS (lst) :
	ans = 0
    for i in lst:
    	DFS(i)
	return ans  

lst = [input()]
print(DFS(lst))

문제에 따라 디테일의 차이가 많겠지만 BFS에 비해 정말 간단하게 구현이 가능하다.

• 리스트 , 배열을 받는다.

• 함수로 재귀를 돌리며 원하는 값을 얻어낸다.

• 원하는 값을 얻어내며 다른 루트에서 얻은 값들과 비교하며 최종답안을 return 한다.

백트래킹

DFS와 문제 구조가 매우 흡사한 알고리즘이다.

def DFS (lst) :
	ans = 0
    for i in range(len(lst)):
    	lst - i
        DFS(lst)
        lst + i
    return

lst = [input()]
print(DFS(lst))

기본적으로는 DFS와 매우 흡사한 모양을 가지게 되는데 한가지 틀린점이 있다.
그건 바로

    	lst - i
        DFS(lst)
        lst + i

이 부분일 것이다.

이렇게 코드를 적은 이유는 다음과 같다.

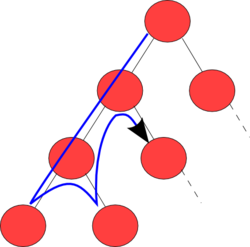
위 트리를 예시로 들자면

• 루트 노드는 밑의 자식 노드 2개를 실행시킬려고 한다.

• 하지만 자식노드는 실행되고 난 후에 바로 종료가 되는것이 아닌 , 자신의 자식을 실행시키려고 한다.

• 이렇게 계속 실행되다보면 결과적으로 제일 왼쪽에 있는 자식이 실행이 된다.

• 제일 왼쪽의 자식의 실행이 완료가 되면 , 그 부모 노드는 다음 자식을 실행시키려고 한다.

• 위의 과정을 반복하게 되면 위의 사진과 같은 실행순서대로 진행이 흘러간다.

• 이러한 과정으로 우리는 모든 경우의 수를 순회하면서 계산 할 수 있는 것이다.

DP

DP는 크게 2가지 방법으로 나뉜다.

# top-down

def fibo (N) :
	if N == 1 or N == 2:
    	return 1
	return f(N-1) + f(N-2)


N = int(input())
print(fibo(N))

첫번째 방법인 top-down 방법이다. memoization을 사용하며 , 코드에서도 알 수 있듯이 구현이 엄청 간단하다. 코드의 흐름은 다음과 같다.

• 함수를 선언한다.

• 함수는 자신을 입력값에서 적절한 조취를 취한 값으로 다시 한번 재귀 돌린다.

• 이러한 과정을 반복하고 , 특정 분기부터 return 한다.

간단하고 구현도 편하다는 장점이 있지만 , 메모리가 터져버린다는 단점이 있다.
간단한 예시로 fibo(1000)만 되어도 메모리나 cpu나 터져버리게 된다.

# bottom-up

a = int(input())
dp = [[for _ in range(M)] for _ in range(N)]

for i in range(N):
	for j in range(M):
    	dp[i][j] = min(dp[i-1][j] , dp[i-1][j-v] + V)

print(dp[-1][-1])

tabulation을 사용하는 bottom-up 방식이다. 계산값을 미리 적어놓고 참조하는 것이라 계산량도 적고 메모리 관리하기도 편하다. 그리고 위의 방법과 비교했을때 상당히 간편해 보인다. 하지만 이 문제는 몇가지 디테일을 잡기 힘들다.

• 점화식을 찾아야 함

• 진행방향을 찾아야 한다.

이렇게 dp는 2가지 방법이 있는데 , 상황에 맞는 알고리즘을 쓰기 위해서는 여러 문제를 보면서 감을 잡아야 한다.

투포인터

lst = []
ans = []
left = 0
right = 0

while True:
	if lst[left] + lst[right] < N:
    	right += 1
        
    else:
    	if lst[left] + lst[right] == N:
        	ans.append([left , right])
    	left += 1
print(ans)

투포인터는 두개의 포인터를 잡고 데이터를 탐색하는 알고리즘이다. 위와 같이 리스트의 부분합을 구하는 문제가 나올 수도 있고 , 두 리스트에 각각 하나씩 배정해서 탐색을 할 수도 있고 여러가지 상황에서 쓰일 수 있다.

그냥 포인터 두개 쓰고(c언어에서 쓰는 포인터와 의미가 같음) 원하는 값을 얻기위해서 사용한다고 보면 된다. 이 알고리즘은 간단하고 범용적이지만 성능은 무시무시한데

브루트포스로 O(n^2)이 나와버리는 부분합 문제도 O(n)으로 만들어버린다..

그리디

시뮬레이션

말 그대로 시뮬레이션 하는 문제들이다.
설명을 더 이상 할게 없으니 예제를 보자.

https://www.acmicpc.net/problem/3190 -> 뱀
https://www.acmicpc.net/problem/13460 -> 구슬탈출2
https://www.acmicpc.net/problem/2638 -> 치즈

정렬

사실 알고리즘의 정의만을 따진다면 여러가지가 있겠지만
파이썬에서 제공하는 sort()의 기능이 너무나도 강력하다.

시간복잡도는 O(nlogn)이며 우리가 풀어야 하는 문제의 난이도를 생각했을때는 굳이 Quick sort의 구현을 배워야 할 필요성은 못느낀다.

단순히 오름차순/내림차순을 해야할때는 그냥 sort()쓰면된다.

덱 , 큐 , 스택

#deque
from collections import deque()

lst = deque() # deque 선언
lst.append(a) # 원소 뒤로 추가
lst.appendleft(b) # 원소 앞으로 추가
A = lst.pop() #뒤의 원소 제거
B = lst.popleft() 앞의 원소 제거

큐 , 스택은 좋긴하지만 코테만 생각했을때는 생각하지 않아도 된다.
그냥 deque 하나면 다 끝난다.
덱 , 큐 , 스택의 정확한 계산량이 어떠한지는 잘 모르지만
코테수준의 문제들은 이러한 것을 생각하지 않아도 된다.

물론 다이아를 노리는 코딩 고수들이라면 정확하게 알긴 해야하지만
아직은 그럴 필요가 없다.

바이너리 서치

def binary(lst:list , find:int):
	# 리스트에서 find 값이 어디인지 위치를 찾는 문제
    # lst의 값은 sort 되어있어야 찾을 수 있다.
	left = 0
    right = len(lst)-1
    mid = (left + right)//2
    while left < right:
    	if lst[mid] < find:
        	left = mid
        elif lst[mid] > find:
        	right = mid
        else :
        	return mid

문제를 풀면서도 놀라는 강력한 도구이다.
bisect를 사용하고 싶어도 사용하지 못하는 경우가 발생하게 되는데 , 이때 사용하는 것이 바이너리 서치이다. 계산량이 O(logn)이라 계산속도도 엄청 빠르고 한두번만 손코딩 해보면 바로 사용할 수 있을만큼 간단한 알고리즘이다.

우선순위 큐

https://blog.encrypted.gg/1015
바킹독의 정석적인 우선순위 큐 강의

thread-safe 해야할때는 priority - queue를 사용해야하지만
코테는 thread-non - safe 환경이라 heapq를 사용하면 된다.

import heapq
# 기본적으로 heapq는 최소힙
lst = [] # heapq.heapify(lst)를 쓰면 원소가 있는 lst도 정렬이 됨.
heapq.heappush(lst , 11) # heapq 배열로 삽입
heapq.heappop(lst) # 최소값 반환

https://www.acmicpc.net/problem/1655

heapq를 활용하는 좋은 문제이다.
기본적인 원리는 최대힙을 만들기 위해 원소를 전부 음수로 만들어버리면
최대값의 음수가 최소값이라는걸 응용하는 것이다.

[1 , 2 , 3 , 4 , 5] # heapq 배열
[-5 , -4 , -3 , -2 , -1] # 음수를 붙이면 heapq배열을 했을때 최대힙이 만들어짐.

그래프

그래프에서 쓰이는 알고리즘을 모아봤다.

• BFS
  https://www.acmicpc.net/problem/2206

• DFS
  https://www.acmicpc.net/problem/2573

• 다익스트라
  https://www.acmicpc.net/problem/2665

• 벨만 - 포드
  https://www.acmicpc.net/problem/1865

• 크루스카
  https://www.acmicpc.net/problem/1197
  크루스카 / 프림은 최소 스패닝 트리의 풀이 알고리즘이다.

• 프림 -> 잘 안쓰임

• 위상정렬
  https://www.acmicpc.net/problem/1005

• 최소 공통조상 LCA(Lowest Common Ancestor)
  https://www.acmicpc.net/problem/11437

정리

코딩 테스트용 간단한 알고리즘을 정리해 봤다.