크래프톤정글0주차 - 배열,재귀함수,빅O til

배열

배열이란?

• 흩어진 코드들을 쉽게 묶어서 사용하기 위한 기능
• 알아볼 자료형 = list,tuple

list

• 리스트 = mutable list형 객체
• 만드는 방법

>>list01 = []
>>list02 = [1,2,3]
>>list03 = ['A','B','C', ] #마지막에 쉼표 써도됨
---------------------
>>list04 = list() #[] 빈 리스트
>>list05 = list('ABC') #['A','B','C']
>>list06 = list([1,2,3]) #list로부터 값 받음
>>list07 = list((1,2,3)) #tuple로부터 값 받음
>>list08 = list({1,2,3}) #집합으로부터 값 받음
>>list09 = [None]*5 #[None,None,None,None,None]
---------------------
* 특이사항
>>list05 = list('ABC') #['A','B','C']
>>list051 = list(['ABC']) #['ABC']
>>list052 = list('ABC',1) #Type error
--> list + tuple

tuple

• 튜플 = immutable 자료형
• 만드는 방법

>>tuple01 = () #빈 튜플
>>tuple02 = 1, #(1,)
>>tuple03 = (1,) #(1,)
---------------------
*주의) 다음은 튜플이 아닌 int형 변수
>>v01 = 1
>>v02 = (1)
---------------------
>>tuple04 = 1, 2, 3 
>>tuple05 = 1, 2, 3, 
>>tuple06 = (1,2,3)
>>tuple07 = (1,2,3, ) # 여백은 상관없음
-> 04~07까지 #(1,2,3)으로 동일
>>tuple08 = 'A','B','C', #('A','B','C')
---------------------
>>tuple09 = tuple() #() 빈 튜플
>>tuple10 = tuple('ABC') #('A','B','C')#각 문자로부터 원소를 생성
>>tuple11 = tuple([1,2,3]) #list로부터 원소를 생성
>>tuple12 = tuple({1,2,3}) #집합으로부터 원소를 생성
---------------------
>>tuple13 = tuple(range(7))
>>tuple14 = tuple(range(3,13,2)) #(3,5,7,9,11)
-> range를 써도 만드는게 가능!

리스트/튜플의 사용

• 풀어내기

>>x = [1,2,3]
>>a,b,c = x
>a,b,c #(1,2,3)

• 인덱스식/슬라이스식 사용

>>x = [1,2,3,4,5,6,7]
>>x[2] # 3
>>x[-1] # 7

>>x[0:6] #[1,2,3,4,5,6]
>>x[0:7:2] #[1,3,5,7]
>>x[-4:-2] #[4,5]
>>x[3:1] #[] *오류는 나지 않음

뮤터블/이뮤터블?

-정말 간단하게 변경가능/변경 불가능이라고 생각하면 된다.
그 이유는 한번 이해하면 절대 까먹지 않을 것이다.

x = [5]
y = [5]
print(id(x),id(y)) #4345347584 4345666560

x = (5)
y = (5)
print(id(x),id(y))#4295993776 4295993776

위 두 식의 차이가 보이는가?
리스트는 id값이 다른 반면, 튜플은 값이 같으면 id값이 같다.
즉 tuple은 자료를 저장하는 것이 아닌, 자료가 있는 위치를 지정해주는 것이다.
그렇기때문에, tuple의 값을 변경하게 되면, 지정해준 위치의 값이 변하게 되는것이고,
그럼 다른 자료들에도 영향을 미치기 때문에 변경 불가능이다.

반대로 list는?
정보를 list에 저장하는 것임으로 변경해도 상관없다.

배열

• .max()
• .min()
• .reverse() #list만 가능, 배열을 역순으로 배열하는것
• reversed()#list, tuple 모두 사용가능, 값을 저장하는것

reverse/reversed 차이
>>x = [1,2,3,4,5]
>>x,reverse()
>print(X) #[5,4,3,2,1]

>>x = [1,2,3,4,5]
>>y = list(reversed(x))
print(y) #[5,4,3,2,1]

이후 진수전환/소수판별은 스킵

재귀 알고리즘

한마디로 요약하면 자신이 자신을 반복한다는 것이다.

def function(n)
	if n == 0 :
    	return 1
    else : 
    	return n*function(n-1)
    
##대충 이런느낌이다.    

자신이 자신을 실행한다 라고 보면 된다.
예제를 풀어보며 좀 더 자세하게 설명해보자.

백준 1914번 하노이탑이다.

하노이탑은 개념만 놓고 보면 참 간단한 문제이다.

• 어찌저찌 해서 모든 디스크를 3번에 큰 디크스부터 작은 디크스 순서로 쌓아라.

근데 이렇게만 적고 보면 식으로 바꾸기 참 힘들다.
그래서 10개를 쌓던 100개를 쌓던 반복되는 부분을 찾아야 한다.
그 방법은 다음과 같다.

1. n번을 제외한 모든 디스크를 2로 옮긴다.
2. n번 디스크를 3으로 옮긴다
3. 2번에 있는 n번을 제외한 모든 디크스를 3으로 옮긴다

이 과정은 n이 2,10,100 .... 어떤 숫자가 들어와도 동일하게 적용된다.
이것을 코드로 적어보자.

def move(no:int,x:int,y:int) -> None:
    if no>1:
        move(no-1,x,6-x-y)
    print(x,y)
    if no>1:
        move(no-1,6-x-y,y)

1. n번을 제외한 모든 디스크를 2로 옮긴다.

    if no>1:
        move(no-1,x,6-x-y)

2. n번 디스크를 3으로 옮긴다.

	print(x,y)

3. 2번에 있는 모든 디스크를 3으로 옮긴다.

    if no>1:
        move(no-1,6-x-y,y)

세세한 과정을 이해하는것이 아닌, 왜 재귀적인 방법으로 풀어지는지에 초점을 맞춰
이해하면 될 것 같다.

Big O(시간복잡도)

알고리즘의 속도는 결과까지 걸리는 절차의 수로 표시한다.

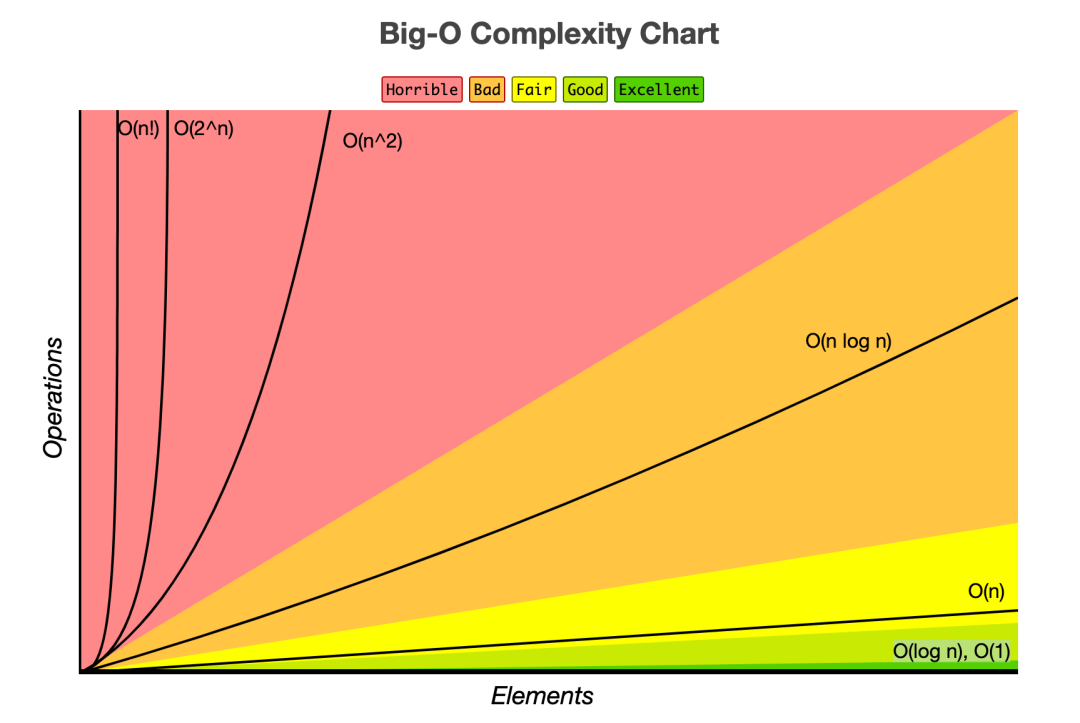
1. O(1) : 스택에서 Push, Pop
2. O(log n) : 이진트리
3. O(n) : for 문
4. O(n log n) : 퀵 정렬(quick sort), 병합정렬(merge sort), 힙 정렬(heap Sort)
5. O(): 이중 for 문, 삽입정렬(insertion sort), 거품정렬(bubble sort), 선택정렬(selection sort)
6. O() : 피보나치 수열