
스택
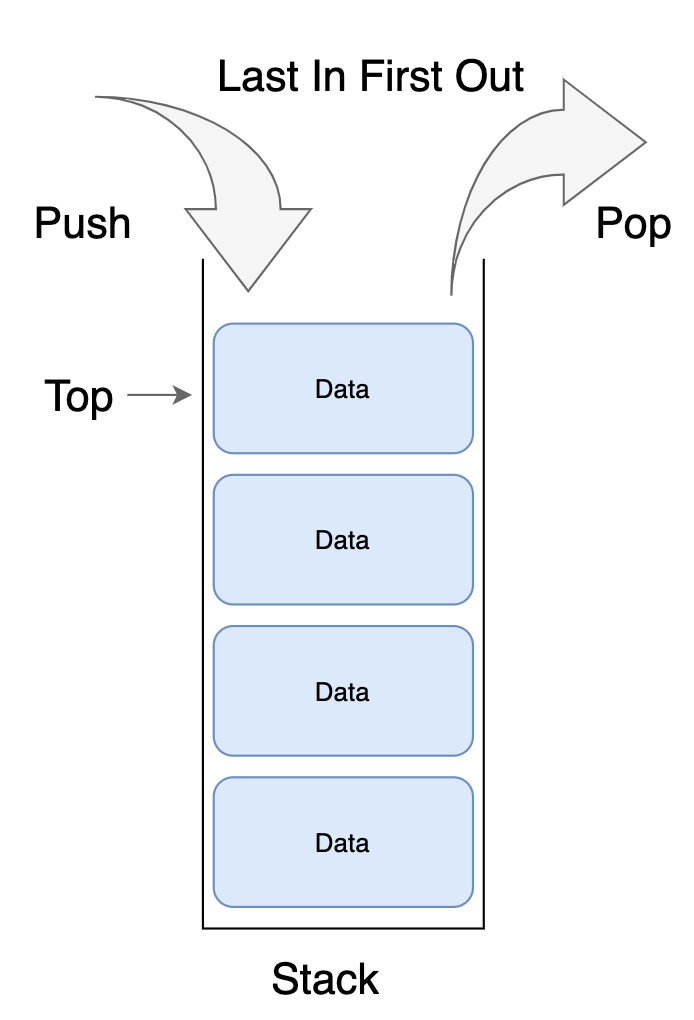
스택을 표현한 그림이다. 사실 다른거 다 필요없이 이 한장에 스택의 모든것이 설명된다고 봐도 과언이 아니다.
다음은 스택의 구조를 알아보자.
- push = 스택에 data를 추가하는 행위이다.
- pop = 스택에서 data를 제거하는 행위이다. 가장 늦게온 data를 우선적으로 제거한다. 즉 가장 먼저 추가된 데이터는 가장 나중에 제거된다.
- capacity = 말 그대로 용량이다. 스택에 10개의 data를 넣을 수 있다면, capacity는 10이다.
- ptr = stack pointer이다. 단순하게 스택에 지금 몇개의 데이터가 쌓여있냐는 것이다. 위 그림에서의 ptr은 4가 된다.
- bottom = 가장 밑부분의 data가 있는 방향을 의미한다. 바닥에 있는 데이터는 위쪽에 데이터가 있는 이상 pop으로는 절대 꺼낼 수 없다.
- top = bottom과는 다르게 가장 최근에 push 한 데이터의 방향이다. 제일 위쪽에 있는 데이터는 가장 최근에 들어온 data이며, pop을 할 시 가장 먼저 제거된다. 이를 last in first out(가장 늦게 들어온 data가 가장먼저나감)이라 한다.
큐
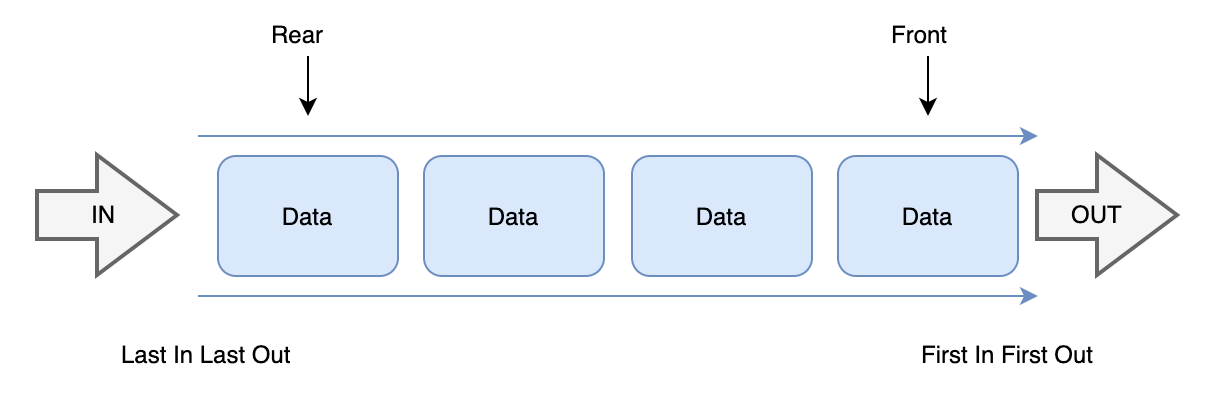
큐를 표현한 그림이다. 스택과 마찬가지로 이 한장에 모든것이 설명된다.
- enqueue = 인큐, 즉 큐에 데이터를 집어넣는 행위이다. 스택과 비슷하게 앞쪽으로 데이터가 쌓인다. 하지만 스택은 bottom으로, 큐는 front로 쌓인다는 차이점이 있다.
- dequeue = 디큐, 큐에서 데이터를 제거하는 행위이다. 디큐는 pop과는 다르게 가장 먼저 들어온 데이터를 가장 먼저 삭제한다. 이를 fifo(first - in - first - out), lilo(last - in - last - out)이라고 한다.
- front = 데이터를 꺼내는 위치를 말한다. 가장 먼저 들어온 데이터가 위치한 곳이기도 하다.
- rear = front와는 다르게 데이터를 추가하는 위치를 말한다. 데이터는 rear에서 front 방향으로 움직이며, front에서 rear방향으로 쌓이게 된다.
우선순위 큐
하나 짚고 넘어가야 할 것이 있다.
이것으로 거의 3시간은 찾은거같은데, 보통 우선순위 큐라고 검색을 하면 많이 나오는것이
'완전이진트리' , '최대/최소 힙'이다.
그래서 처음에 생각했을때는
'완전이진트리는 뭐 이런 구조이고... 완전이진트리로 만든 최대/최소 힙이 우선순위 큐인것인가?'
라는 고민을 했고, 이것때문에 시간이 엄청 오래 끌렸다.
하지만, 우선순위 큐는 추상적인 개념일뿐이고, (우선순위 큐는 "리스트"나 "맵"과 같이 추상적인 개념이다 - 위키) 그러한 개념을 최대/최소 힙이라는 방법을 통해서 구현한 것일 뿐이다.
설명은 정말 금방 끝난다.
- 우선순위 큐라는건 뭔데? -> 각 원소들이 우선순위를 가지고 있고, 높은 우선순위를 가진 원소가 먼저 처리되는 자료형.
이라고 생각하면 된다.
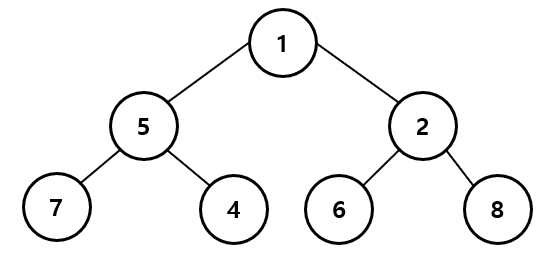
다음은 우선순위 큐의 종류 중 하나인 최소 힙이다.
각각의 원소들은 위로 하나, 아래로 둘의 원소와 이어질 수 있는데,
이때 위의 원소는 부모 노드, 아래의 원소는 자식노드 라고 한다.
정말 간단한 원칙 하나만 정하면 된다.
최소 힙 = 부모 노드의 key는 자식 노드의 key 보다 작으면 된다.
최대 힙 = 부모 노드의 key는 자식 노드의 key 보다 크면 된다.
이해가 되는가? 위 그림에서 상단의 1-(5,2)를 보도록 하자.
부모 노드인 1은 자식 노드인 5,2 보다 작다.
이걸 전체 노드에 정하면 되는 것이다.
그리고 데이터를 추가하고자 한다면, 왼쪽부터 오른쪽 순으로 자식노드를 채우고,
한 줄이 다 찼으면 다음줄부터 채우면 된다.
위의 그림에서는 새로운 7 노드의 왼쪽부터 채우면서, 8 노드의 오른쪽까지 모두 채우고 나면
다음줄을 채우면 된다는 것이다.
여기서 내가 궁금해 했던것은 '그럼 자식 노드들 간에 숫자 차이는 어떻하지?' 라는 것이었다.
하지만 그런건 어차피 별 상관이 없었는데, 트리가 어떻게 정렬이 되어 있던 우리가 원하는
'우선순위 별로 데이터를 처리한다'만 해결되면 되기 때문에
이 기능만 잘 작동한다면 나머지 데이터가 어떻게 정렬되어 있던 아무런 상관이 없다.
그래서 이러한 방법을 통해 우리는 시간복잡도를 n -> logn으로 줄일 수 있게 되었다.
