마코프 체인(Markov chain; 마르코프 연쇄)은 현재의 데이터를 기반으로 미래를 예측하는 모델링이라고 할 수 있다.
(A Markov chain is a sequence of events in which the probability of the next event depends only on the state of the current event.)
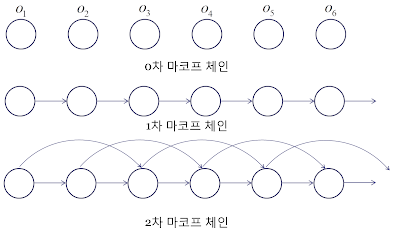
Markov property
마코프 체인은 마코프 성질을 가지는데, 마코프 성질이란 시스템의 과거 상태 와 현재 상태 가 있을 때, 미래 상태 가 현재 상태 에 의해서만 결정되는 성질이다. (각 는 discrete하게 변한다.)
이에 따르면 는 에 의해 결정되고, 은 에 의해 결정되고, ..., 은 에 의해 결정되기 때문에 결국 마코프 성질은 현재 데이터가 과거 데이터를 내포한다는 의미가 된다. 이를 다시 말하면 과거 상태들을 고려한 조건부 확률과 현재 상태만을 고려한 조건부 확률이 동일하다.
예를 들어 날씨가 마코프 성질을 따른다고 가정해보자. (더욱 복잡한 물리 변수들의 상호작용 때문에 실제로 마코프 성질을 따르지는 않는다고 함) 마코프 성질에 따르면, 내일의 강수 확률을 계산할 때 오늘의 습도를 고려한 강수 확률과 일주일 전부터 오늘까지의 습도를 고려한 강수 확률이 같게 된다.
구성 요소
마코프 체인은 상태 공간(state space), 전이 확률(transition probability), 전이 행렬(transition matrix), 초기 상태 분포(initial distribution)으로 구성된다.
상태 공간
가능한 모든 상태들의 집합을 말한다. 날씨의 예로 보면 상태 공간 = {맑음, 비, 눈, 강풍, ...}으로 표현할 수 있다.
전이 확률 & 전이 행렬
전이 확률은 한 상태에서 다른 상태로 변화할 확률이다. 로 상태가 변할 때 확률을 라고 하면
라고 표현한다.
전이 행렬은 전체 상태 간 전이 확률을 행렬로 표현한 것이다.
예를 들어 날씨의 전이 행렬을 만들어보자. 아래 표에 따르면 오늘이 맑을 때 내일도 맑을 확률이 0.8이고, 내일은 비 올 확률이 0.2이다. 오늘이 비가 올 때 내일은 맑을 확률이 0.4, 비가 올 확률은 0.6이다.
| 맑음 | 비 | |
|---|---|---|
| 맑음 | 0.8 | 0.2 |
| 비 | 0.4 | 0.6 |
이를 행렬로 표현한 것이 전이 행렬이다.
초기 상태 분포
시작할 때의 상태 확률 분포이다.
확률 계산
전이 행렬이 , 초기 상태 분포를 라 하면 t일 후의 상태 분포 는 와 같다.
수렴 성질과 정적 분포
초기 상태에 상관 없이, 시간이 충분히 지나면 상태 확률 분포가 수렴하게 된다. 이를 정적 분포(Stationary Distribution)라고 한다.
위의 확률 계산 식에서, 로 가면 이 일정한 행렬로 수렴하게 되고, 따라서 확률 분포가 특정 값으로 고정된다. 가 일정한 행렬로 수렴하는 이유는, 전이 행렬 가 확률 행렬로써 모든 원소가 0 이상의 값을 갖고 각 행은 원소의 합이 1인 하나의 확률 분포여서 항상 가장 큰 고유값 을 갖기 때문이다. 나머지 고유값들은 절대값이 1보다 작기 때문에, 이 되면서 영향이 사라지고 인 부분만 남고, 이 고유값에 해당하는 고유 벡터가 정적 분포가 된다.
코드로 이해하기
날씨를 예측하는 마코프 체인 시뮬레이션을 해보자. 편의상 날씨가 마코프 체인 성질을 지니고, {sunny, cloudy, rainy}의 3개 요소의 상태 공간으로 이루어져 있다고 가정하자. 이 때의 전이 행렬은 아래 표와 같은 형태라고 하자.
| From/to | sunny | cloudy | rainy |
|---|---|---|---|
| sunny | 0.7 | 0.2 | 0.1 |
| cloudy | 0.3 | 0.4 | 0.3 |
| rainy | 0.2 | 0.3 | 0.5 |
import numpy as np
import random
# 상태 공간
states = ['sunny', 'cloudy', 'rainy']
state_to_idx = {state:i for i, state in enumerate(states)}
# 전이 행렬
transition_matrix = [
[0.7, 0.2, 0.1], # from sunny
[0.3, 0.4, 0.3], # from cloudy
[0.2, 0.3, 0.5] # from rainy
]
def next_state(current_state):
return np.random.choice(states, p=transition_matrix[state_to_idx[current_state]])
def markov_chain(start='sunny', n_days=15):
sequence = [start]
current = start
for _ in range(n_days-1):
current = next_state(current)
sequence.append(current)
return sequence
# 마코프 체인 시뮬레이션 실행
weather_sequence = markov_chain(start='sunny', n_days=15)
print(" → ".join(weather_sequence)
# sunny → cloudy → cloudy → cloudy → cloudy → rainy → cloudy → sunny → rainy → cloudy → cloudy → cloudy → cloudy → sunny → cloudy위와 같이 파이썬 코드로 마코프 체인 시뮬레이션을 실행해서 처음 상태가 맑음이었을 때 그 다음에 어떤 날씨 상태가 되는지 확인해볼 수 있다.
위의 정적 분포 부분에서 살펴본 것처럼, 시간이 충분히 지나면 상태 확률 분포가 수렴하게 된다. 이를 실제로 계산해서 확인해보자.
import matplotlib.pyplot as plt
# 초기 상태 분포: 맑음에서 시작
state = np.array([1.0, 0.0, 0.0])
# 시간에 따른 상태 분포 기록
states_over_time = [state]
for _ in range(50):
state = @ transition_matrix
states_over_time.append(state)
states_over_time = np.array(states_over_time)
# 그래프 그리기
plt.plot(states_over_time[:, 0], label='sunny')
plt.plot(states_over_time[:, 1], label='cloudy')
plt.plot(states_over_time[:, 2], label='rainy')
plt.xlabel('number of days')
plt.ylabel('Probability')
plt.title('Markov chain example (weather)')
plt.grid(True, ls='--', alpha=0.5)
plt.legend()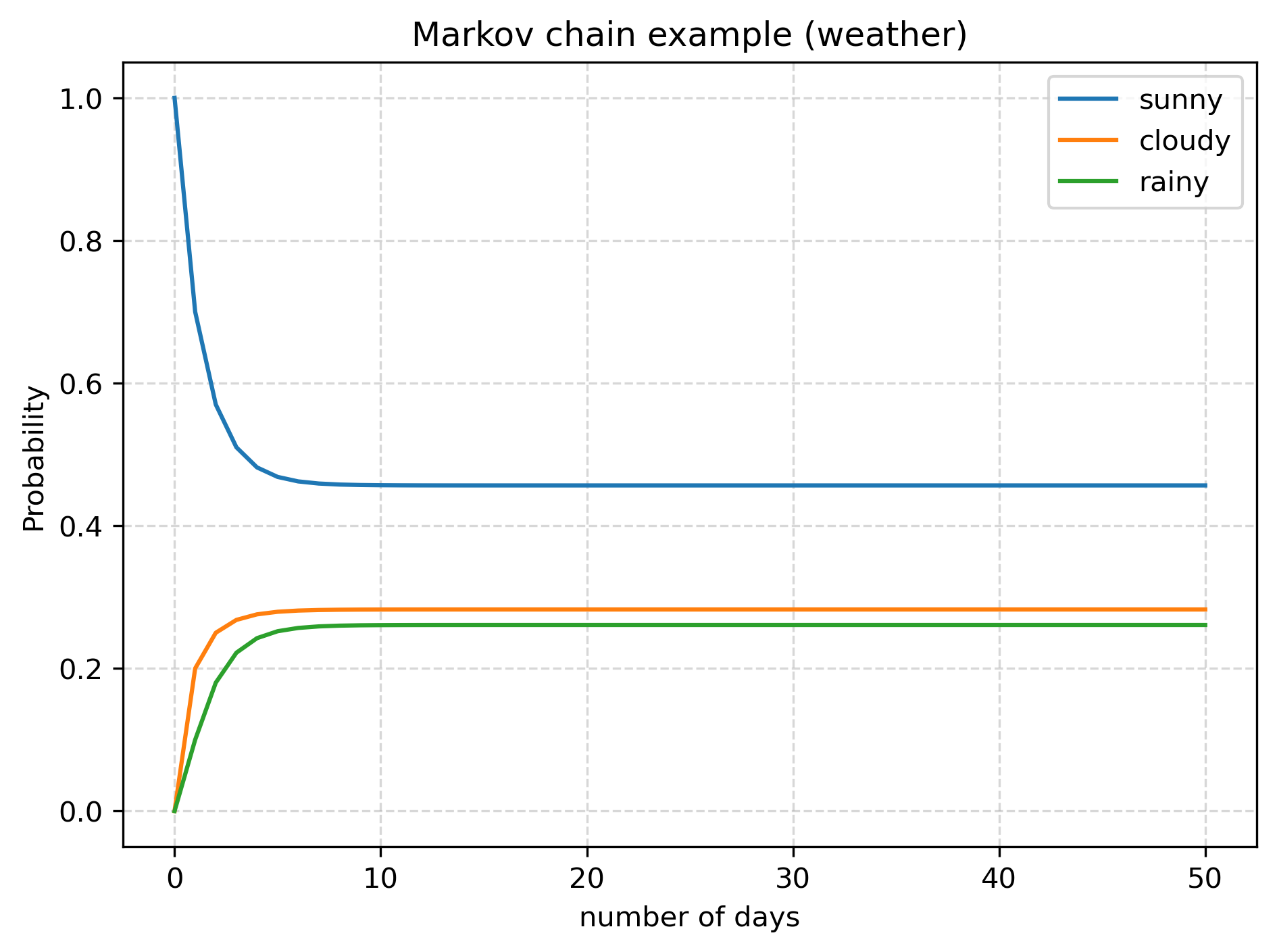
처음에는 맑음, 흐림, 비 = 1, 0, 0의 확률이었지만 시간이 많이 지나면서 맑음, 흐림, 비 = 0.4565, 0.2826, 0.2608으로 값이 수렴하는 것을 확인할 수 있다.
적용
강화 학습
강화 학습은 에이전트가 어떤 상태가 있고, 행동을 선택하여 다음 상태로 전이하면서 보상을 받는 구조로 이루어진다. 이 때 다음 상태와 보상이 현재 상태와 행동으로 결정되기 때문에, 마코프 성질을 가진다고 할 수 있다.
텍스트 생성 (언어 모델링)
앞의 n개 단어를 보고 다음 단어를 예측하는 것에 n차 마코프 모델이 적용된다.
ex) n-gram
References
https://velog.io/@nochesita/%ED%99%95%EB%A5%A0%ED%86%B5%EA%B3%84-%EB%A7%88%EB%A5%B4%EC%BD%94%ED%94%84-%EC%B2%B4%EC%9D%B8-Markov-Chain
https://people.duke.edu/~ccc14/sta-663-2018/notebooks/S10B_MarkovChains.html
https://m.blog.naver.com/jinis_stat/221686989847
https://wikidocs.net/203336
https://roytravel.tistory.com/358
https://velog.io/@qkrdbwls191/Markov-chain
