🌈 클로저 closure

클로저란 폐쇠된 공간 안에 데이터에 접근하기 위한 테크닉입니다.

좀 더 풀어서 얘기하자면, 외부 함수에 대한 접근 권한을 내부 함수에 위임함으로서 폐쇠된 공간 안의 데이터에 접근할 수 있도록 하는 테크닉입니다

예제 1

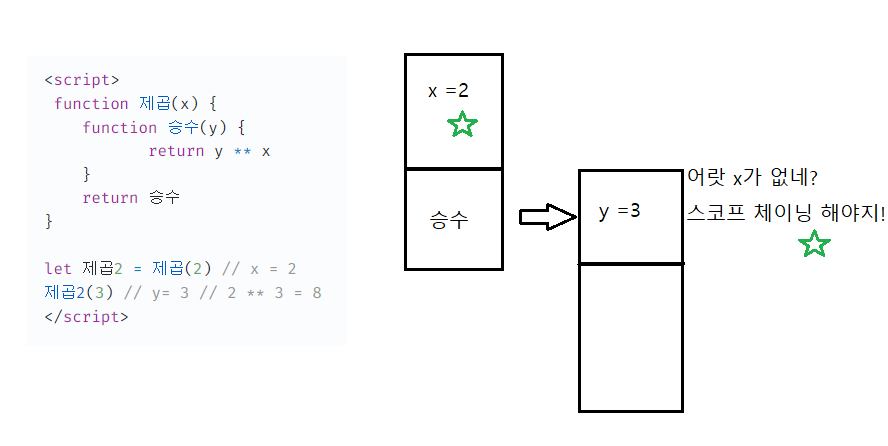
즉, 클로저란 여기서 폐쇠된 function 승수에 접근해서 활용할수있는 테크닉이다.

예제 2

add5, add10이 클로저입니다.

<script>
function makeAdder(x) {
    var y = 1;
    return function(z) {
        y = 100;
        return x + y + z;
    };
}

var add5 = makeAdder(5);
var add10 = makeAdder(10);
//클로저에 x와 y의 환경이 저장됨

console.log(add5(2));  // 107 (x:5 + y:100 + z:2)
console.log(add10(2)); // 112 (x:10 + y:100 + z:2)
//함수 실행 시 클로저에 저장된 x, y값에 접근하여 값을 계산
//지역스코프에서 값을 찾고, 없으면 그 밖에 있는 스코프에서 찾고, 계속해서 찾아 올라가 전역 스코프까지 찾아보는 것을 스코프체이닝
//어려운 얘기로는 내부 렉시컬 환경에서 찾고 없으면 전역 렉시컬 환경에서 찾는다 얘기함.
//함수가 수행된 이후에도 상위함수의 렉시컬 환경에 접근 가능
</script>

예제 3

<script>
function 제곱(x) {
    function 승수(y){
        return y ** x
    }
    return 승수
}

let 제곱2 = 제곱(2) //2 제곱해주는 함수 //x에 2가 들어간거에요

function 제곱(2) {
    function 승수(y){
        return y ** 2
    }
    return 승수 //함수를 리턴함
}




let 제곱3 =  제곱(3) //3 제곱해주는 함수 //x에3 들어간거에요
let 제곱4 =  제곱(4) //4 제곱해주는 함수 //x에4 들어간거에요

제곱2(2) //x에 2, y에 2       //반환값: 4
제곱2(3) //x에 2, y에 3      //반환값: 9
제곱2(4) //x에 2, y에 4// 제곱(2)(4) //2의 4승...16
제곱3(3) //x에 3, y에 3     //반환값:27
제곱4(3) //x에 4, y에 3 //3x3x3x3 //반환값:81

</script>

예제 4

<script>
//함수를리턴해줄수있음을 나타내는 예제
function 리턴함수(){
    function sum(a,b) {
        return a+b
    }
    return sum
}

let 합 = 리턴함수()
합(2,3) //5

//함수부분이 1001 // (a,b) {}이부분
//sum ->1001
//합 -> 1001



</script>

예제 5

<script>

function closure() {
  let cnt = 0;
  function cntPlus(){
    cnt = cnt + 1;
  }
  function setCnt(value){
    cnt = value;
  }
  function printCnt(){
    console.log(cnt);
  }
  return {
    cntPlus,
    setCnt,
    printCnt,
  }
}

const cntClosure = closure();

console.log(cntClosure.printCnt()); //0, undefined 출력
cntClosure.cntPlus();
cntClosure.setCnt(100);
cntClosure.printCnt(); //100

</script>