7. Kernel method

KVV·2025년 2월 5일

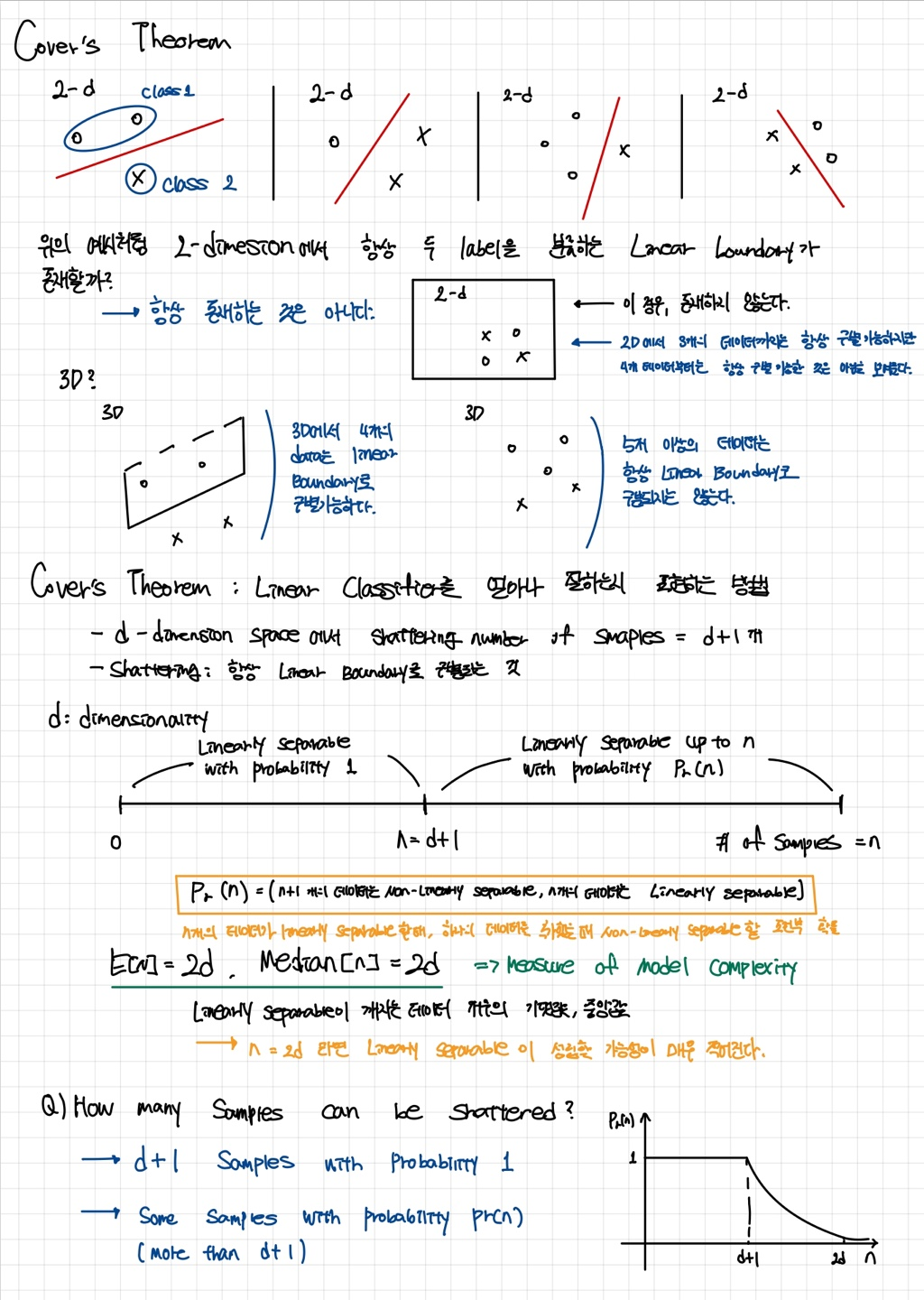
Cover's theorem

d-차원에서는 (d+1) 개의 데이터를 완벽하게 선형 분류할 수 있으며, d-차원에서 Linearly separable한 데이터의 평균값은 2d이다.

Kernel method

Cover's theorem 에서 확인한 것처럼, Low-dimension을 High-dimension으로 확장하면 복잡한 데이터도 Linearly seperable 가능하다는 믿음에 근거해 Low-dimension 에서 High-dimension을 다루기 위한 방법

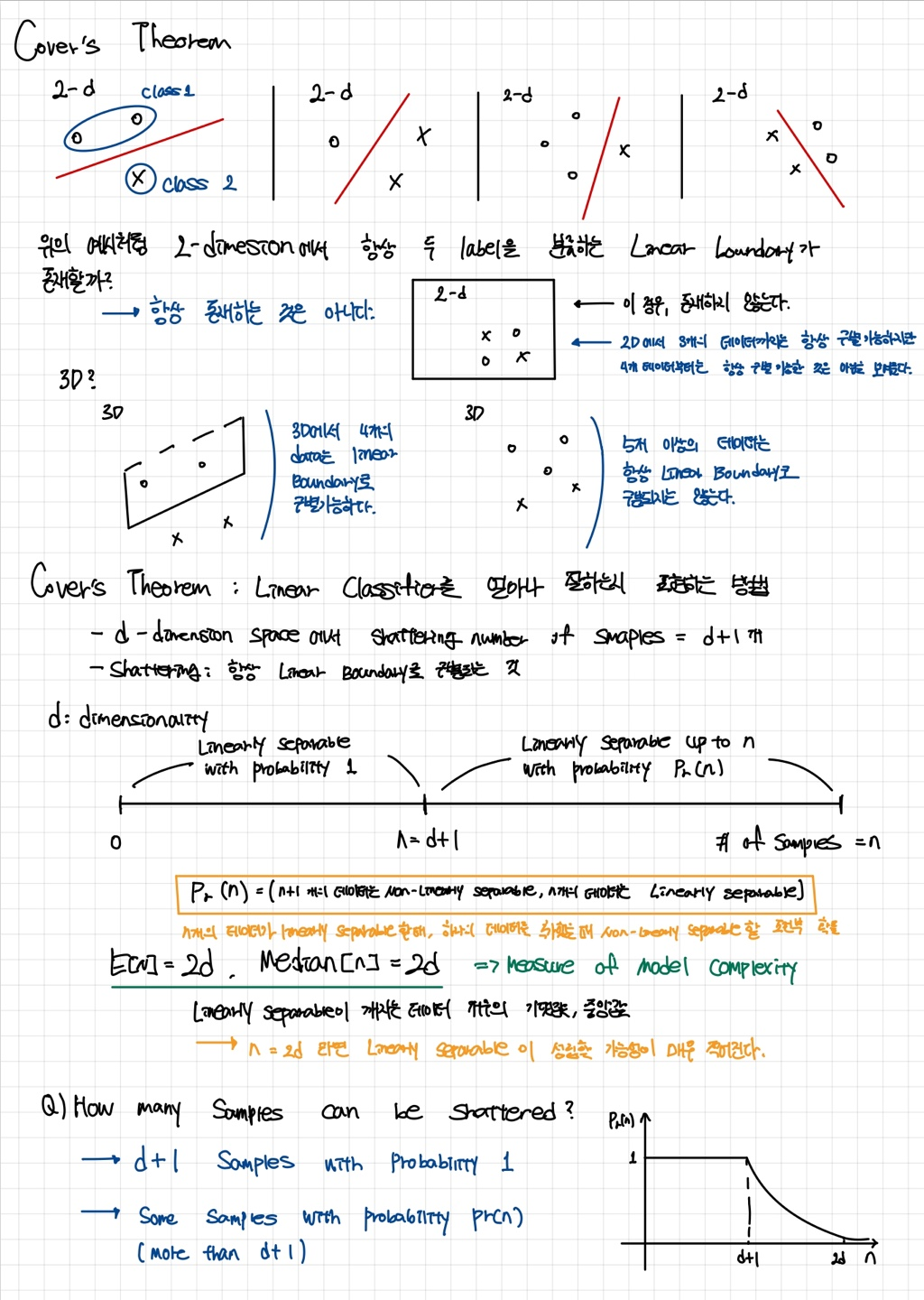
Kernel method의 기본 원리는 다음과 같다. 데이터가 원래 d차원(특성의 개수가 d)인 경우, 각 데이터 포인트 $x_i$ , $i = (1, ... d)$ 를 선형 조합하여 고차원 k차원 (k>d)으로 매핑하는 함수 Φ를 정의한다. 이 매핑 함수들끼리 내적을 수행하면, 고차원 공간에서의 연산을 원래의 저차원에서 수행할 수 있게 되어, 효율적으로 계산할 수 있다.

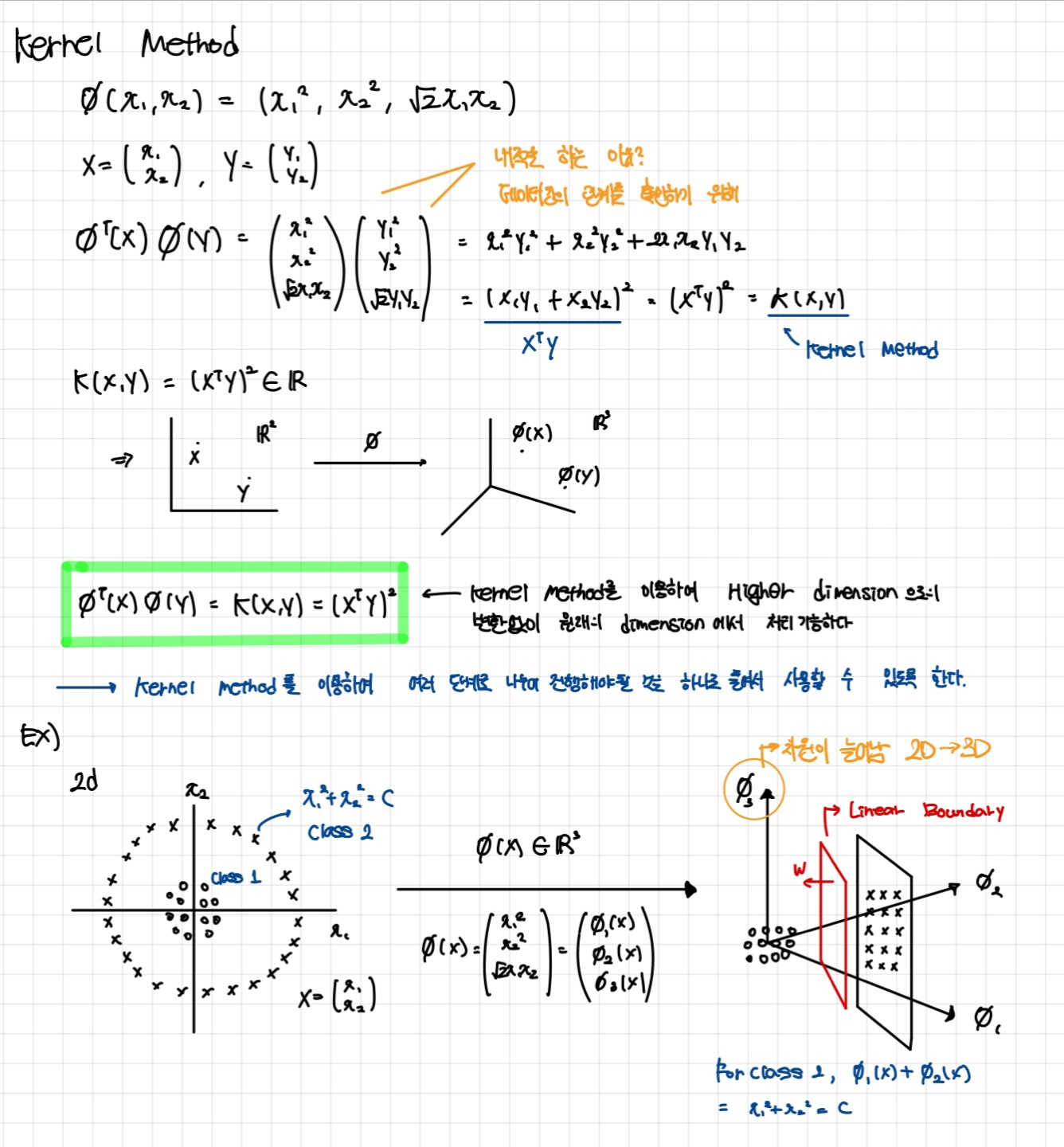
$x_1, x_2$ 를 이용하여 매핑 함수를 정의하고, 매핑 함수의 내적을 Kernel function 으로 간단히 정리한다.
Kernel function만을 이용하면 매핑 함수를 이용하여 고차원을 다루는 것과 같은 효과를 낼 수 있다.
- Kernel method가 위와 같은 결과를 만들 수 있는 이유는 매핑 함수의 내적과 Kernel method의 계산 결과가 동일하기 때문이다.
- 해당 그림은 2차원에서 Liearly separable 하지 않던 데이터가 3차원에서는 Linearly separable 가능한 예시를 보여준다.

Kernel method는 고차원에서의 표현을 실제로 만들지 않고 Kernel method의 계산 결과만 사용하면 된다는 이점이 있다.

Kernel method는 내적을 이용하므로 유사도 함수 (Similarity function) 으로 해석할 수도 있다. 각 Kernel의 식을 살펴보면 거리를 측정하는 느낌을 받을 수 있다. Kernel method는 각 kernel의 상수를 이용하여 거리가 가까운 것에 큰 유사도 점수를, 먼 것에 작은 유사도 점수를 부여하는 방식으로 동작한다.

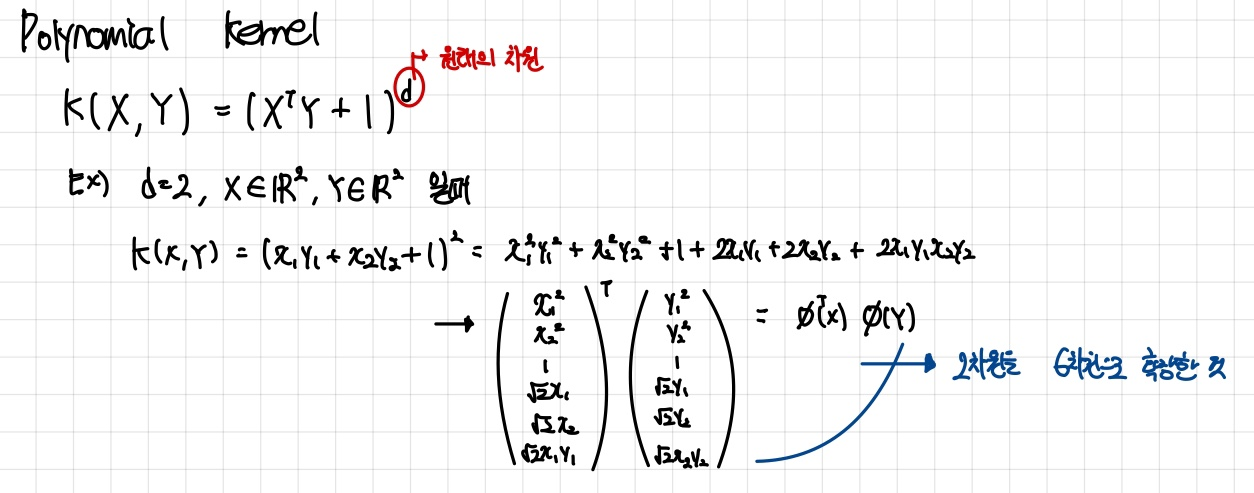
Polynomial kernel

데이터 포인트들 간의 내적을 다항식 함수로 확장한 형태

사이킷런으로 Polynomial kernel 구현

import sklearn.svm import SVC

#X_xor, y_xor: 비교적 random 하게 분포되어있는 데이터셋
# kernel = 'poly'
svm = SVM(kernel='poly', random_state=1, C=10.0)
svm.fit(X_xor, y_yor)

Gaussian kernel

두 데이터 포인트 사이의 거리를 기준으로 두 데이터 포인트 사이의 유사성을 측정하는 함수

Gaussian kernel은 두 벡터의 유클리드 거리라고도 생각할 수 있다.

사이킷런으로 Gaussian kernel 구현

import sklearn.svm import SVC

# kernel = 'rbf' 
# Radial basis function 의 줄임말으로 Gaussian kernel의 다른 표현
# gamma=: Gaussian shpere 의 크기를 조절
svm = SVM(kernel='rbf', random_state=1, gamma = 0.10, C=10.0)
svm.fit(X_xor, y_yor)

$\gamma = \frac{1}{2 \sigma^2}$ 으로 나타낼 수 있다.
Underfitting: $\gamma$ 가 너무 작고 $\sigma$ 가 너무 큰 경우
Overfitting: $\gamma$ 가 너무 크고 $\sigma$ 가 너무 작은 경우
- Support vector의 영향이나 범위가 줄어든다.

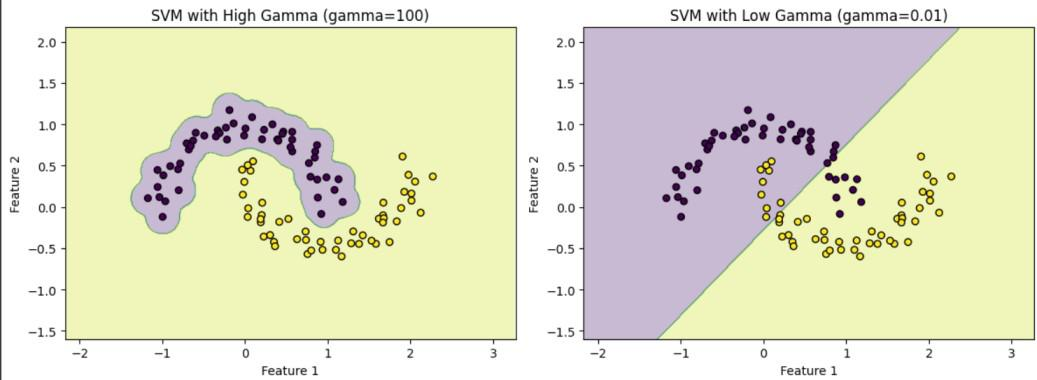
이 그림에서 보듯이 gamma가 큰 경우에 결정 경계가 샘플에 가까워지고, 구불구불해지는 것을 확인할 수가 있다.

Kernel method로 SVM 해결

Kernel method를 이용하여 Nonlinearly separable 한 데이터를 SVM으로 Linearly separate 할 수 있다. 수학적인 증명을 알아보자.

사이킷런의 SVC class의 parameter kernel = " "은 해당 식에서 사용될 Kernel method의 종류를 선택하는 것이다.

다른 방법

Mapping function은 $x_i$ 를 고차원으로 확장하기 위해 $x_i$ 대신 사용하는 것이다.

Mercer's theorem

Kernel method가 만족해야하는 정리로 Mapping function을 직접 구하지 않아도 Kernel method를 사용할 수 있음을 확인할 수 있다.

Kernel method는 상수값을 출력하는 연속 함수이다.
Kernel matrix는 Symmetric이고 Positive semi-definite라면, 위 식을 만족하는 어떤 Mapping function이 존재한다.

Positive definite matrix

Eigenvalue가 양수인 Symmetric matrix를 의미한다.

가장 유명한 조건은 0이 아닌 벡터 x에 대해 $X^TAX > 0$ 이라면, A는 Positive definite matrix라는 것이다.

Kernel matrix

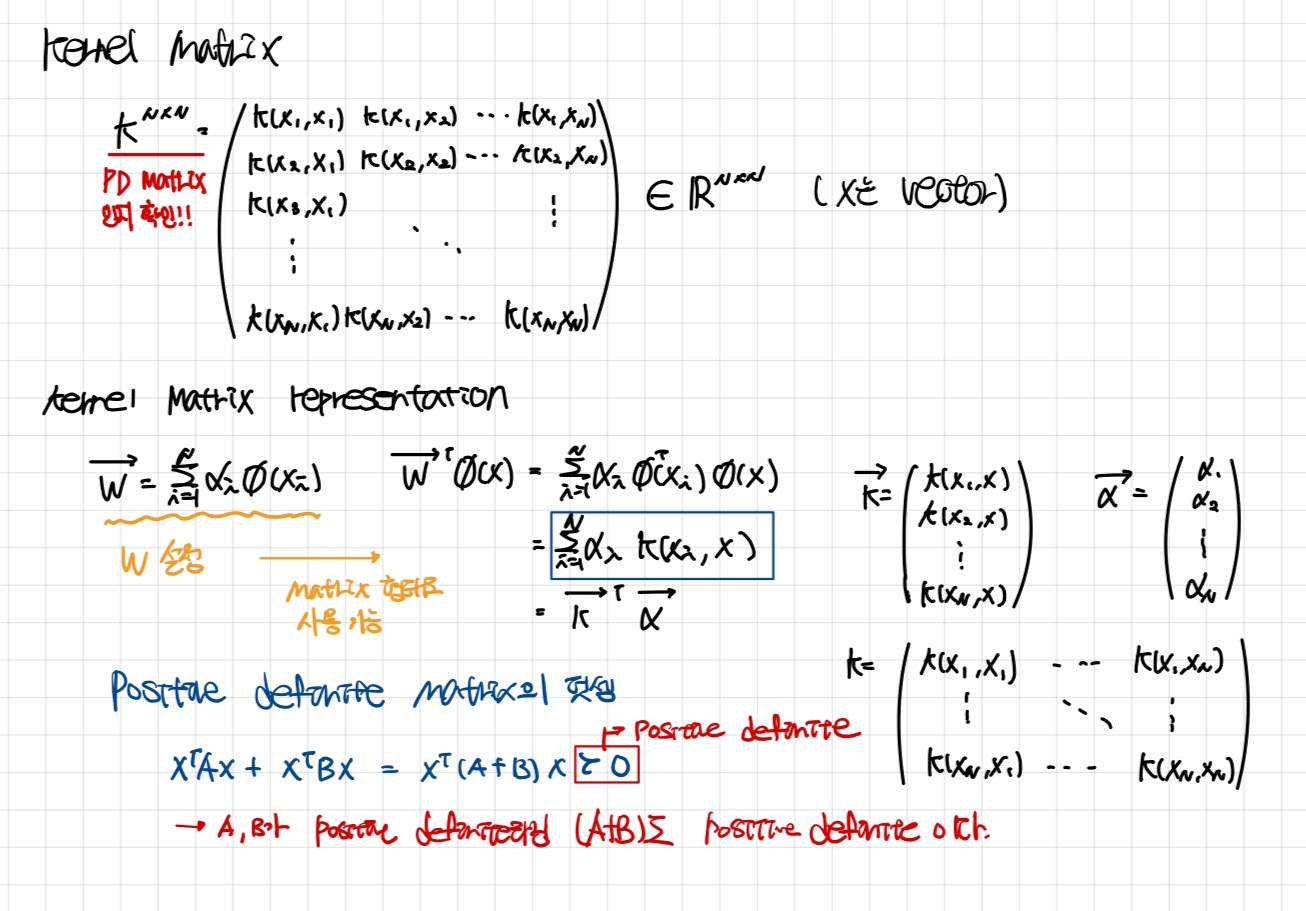
우리는 kernel method를 이용하기 위해, $w$ vector를 위처럼 정의할 수 있다.
$W^T\Phi(X)$ 는 단순한 커널 함수들의 선형 조합으로 표현된다.
- Positive definite matrix의 덧셈으로 이루어진 행렬도 Positive definite martix임을 위에서 확인할 수 있다.
$W^TW$ 는 Kernel martix의 형태로 표현된다.
- 이 또한 Positive definite 임을 확인할 수 있다.

여러 방법을 사용하여 kernel matrix가 Positive definition 임을 확인할 수 있다.

Representer theorem

모델의 해를 데이터 샘플의 커널 함수의 선형 조합으로 표현할 수 있음을 보장하는 정리

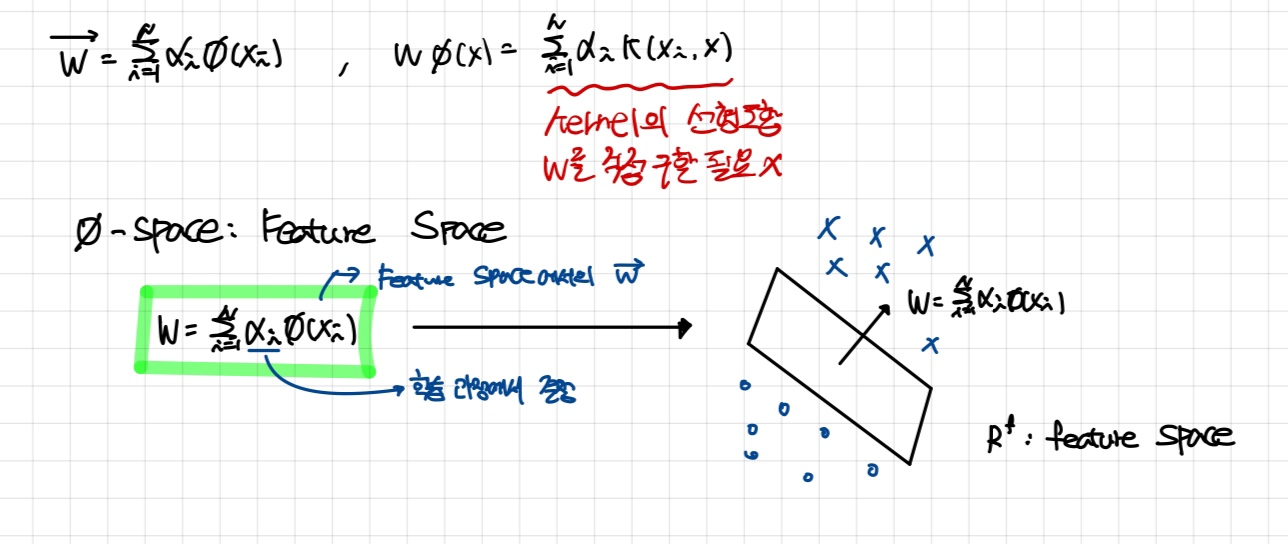
위 그림에서처럼 $w$ 를 $\Phi$ 에 대해 표현한다면, $W^T\Phi(X)$ 는 kernel method의 선형 조합으로 나타낼 수 있다.
즉, 데이터 X 를 $\Phi$ 로 나타나는 feature space로 classification 할 수 있다는 뜻이다.

Logistic regression with kernel method

Parameter의 개수가 Kernel method를 사용하지 않을 때보다 현저히 줄어든 것을 확인할 수가 있다.
- f + 1 dimension -> N + 1 dimension
- Mapping function을 이용하여 확장한 차원 (f dimension)을 데이터의 개수 (N개) 로 표현할 수 있다.