[프로그래머스] ⭕두 원 사이의 정수 쌍

😀문제 설명

x축과 y축으로 이루어진 2차원 직교 좌표계에 중심이 원점인 서로 다른 크기의 원이 두 개 주어집니다. 반지름을 나타내는 두 정수 r1, r2가 매개변수로 주어질 때, 두 원 사이의 공간에 x좌표와 y좌표가 모두 정수인 점의 개수를 return하도록 solution 함수를 완성해주세요.
※ 각 원 위의 점도 포함하여 셉니다.

---

😁제한 사항

• 1 ≤ r1 < r2 ≤ 1,000,000

---

😂입출력 예

r1	r2	result
2	3	20

---

🤣입출력 예 설명

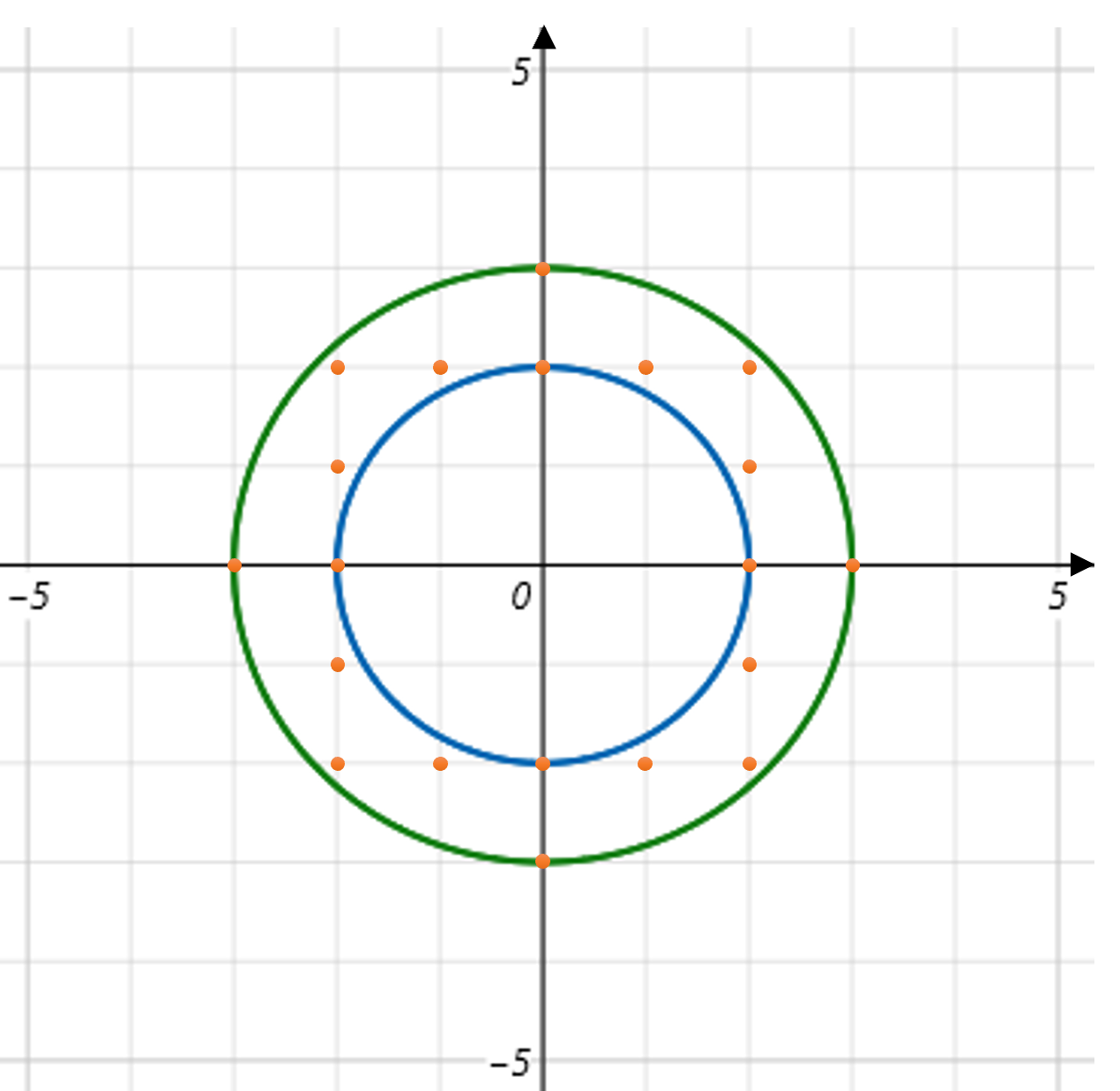
그림과 같이 정수 쌍으로 이루어진 점은 총 20개 입니다.

---

😄나의 풀이

첫 풀이는 이러하다. 완벽한 로직이라 생각했으나 시간 초과.. 질문하기를 살펴보니 long 타입을 선언해야 한다는 말을 보자마자

제한 범위가 상당히 큰 문제라는 것을 깨달았다.

function solution(r1, r2) {
  let count = 0;

  // 큰 원의 범위는 원점에서 -r2(원점 - 반지름) ~ r2(원점 + 반지름) 까지이며,
  for (let x = -r2; x <= r2; x++) {
    // 작은 원의 범위는 원점에서 -r1(원점 - 반지름) ~ r1(원점 + 반지름) 까지이다.
    for (let y = -r2; y <= r2; y++) {
      // 피타고라스의 정리를 통해 원점에서 현재 점의 거리는 x^2 + y^2
      const distance = x * x + y * y;
      // 현재 점의 거리가 작은 원 보다 멀고 큰 원의 범위 안 이라면 카운트
      if (distance >= r1 * r1 && distance <= r2 * r2) {
        count++;
      }
    }
  }

  return count;
}

찾아보니, 원점과의 거리를 계산해서 계산하는 문제였음. 정말 공교롭게도 완벽한 풀이에 실패한 문제이다.

다른분의 풀이를 봐보자

하나의 사분면 위에 위치한 점의 개수를 파악한 후 마지막에 *4를 함으로써 점의 개수를 완벽히 알아내셨다

나도 노력해야할듯

function solution(r1, r2) {
    var answer = 0;
    for (var x=1;x<=r2;x++) {
        var min = r1 >= x ? Math.ceil(Math.sqrt(r1*r1-x*x)) : 0;
        var max = Math.floor(Math.sqrt(r2*r2-x*x));
        answer += max-min+1;

    }
    return 4*answer;
}