1: Definition
n n n ( x 1 , x 2 , . . . , x n ) (x_1, x_2, ... , x_n) ( x 1 , x 2 , . . . , x n ) x i , i ∈ R x_i,\quad i\in\mathbb{R} x i , i ∈ R n n n n − t u p l e s n-tuples n − t u p l e s E n E^n E n n n n n n n
2: Definition
두개의 유클리드 n n n ( x 1 , ⋯ , x n ) + ( y 1 , ⋯ , y n ) = ( x 1 + y 1 , ⋯ , x n + y n ) (x_1, \cdots , x_n) + (y_1, \cdots ,y_n)=(x_1+y_1, \cdots ,x_n+y_n) ( x 1 , ⋯ , x n ) + ( y 1 , ⋯ , y n ) = ( x 1 + y 1 , ⋯ , x n + y n )
만약 a ∈ R a\in\mathbb{R} a ∈ R ⟺ α ∈ E n \iff \alpha\in E^n ⟺ α ∈ E n α ⋅ ( x 1 , ⋯ , x n ) = ( α x 1 , ⋯ , α x n ) \alpha \cdot (x_1, \cdots,x_n)=(\alpha x_1, \cdots ,\alpha x_n) α ⋅ ( x 1 , ⋯ , x n ) = ( α x 1 , ⋯ , α x n ) α x 1 \alpha x_1 α x 1 α \alpha α x 1 x_1 x 1
3: Proposition
우선 X , Y , Z , θ ∈ E n X, Y, Z, \theta \in E^n X , Y , Z , θ ∈ E n α , β ∈ R \alpha, \beta \in \mathbb{R} α , β ∈ R
X = ( x 1 , ⋯ , x n ) , Y = ( y 1 , ⋯ , y n ) Z = ( z 1 , ⋯ , z n ) , θ = ( 0 , ⋯ , 0 ) X = (x_1, \cdots, x_n),\qquad Y = (y_1, \cdots, y_n)\\ Z = (z_1, \cdots, z_n),\qquad \theta = (0, \cdots, 0) X = ( x 1 , ⋯ , x n ) , Y = ( y 1 , ⋯ , y n ) Z = ( z 1 , ⋯ , z n ) , θ = ( 0 , ⋯ , 0 ) 그러면, 다음과 같은 명제가 성립한다.
a) ( X + Y ) + Z = X + ( Y + Z ) ⋯ (X + Y)+Z = X+(Y+Z) \quad \cdots ( X + Y ) + Z = X + ( Y + Z ) ⋯ X + θ = X X+\theta=X X + θ = X X + Y = Y + X X+Y=Y+X X + Y = Y + X X + ( − 1 ) X = θ X+(-1)X = \theta X + ( − 1 ) X = θ ( α + β ) ⋅ X = α ⋅ X + β ⋅ Y (\alpha+\beta)\cdot X=\alpha \cdot X + \beta \cdot Y ( α + β ) ⋅ X = α ⋅ X + β ⋅ Y α ⋅ ( X + Y ) = α ⋅ X + α ⋅ Y \alpha \cdot(X+Y) = \alpha \cdot X + \alpha \cdot Y α ⋅ ( X + Y ) = α ⋅ X + α ⋅ Y ( α ⋅ β ) ⋅ X = α ⋅ ( β ⋅ X ) (\alpha \cdot \beta)\cdot X = \alpha \cdot(\beta \cdot X) ( α ⋅ β ) ⋅ X = α ⋅ ( β ⋅ X ) 1 ⋅ X = X 1 \cdot X = X 1 ⋅ X = X
1) E n E^n E n E n E^n E n E 1 = R E^1=\mathbb{R} E 1 = R θ = ( 0 , 0 , ⋯ , 0 ) \theta=(0,0,\cdots,0) θ = ( 0 , 0 , ⋯ , 0 )
3)문장이 상당히 모호할 수 있다. 간단히 설명하자면 E 1 E^1 E 1 α , β \alpha, \beta α , β α < β \alpha<\beta α < β α > β \alpha>\beta α > β ( a , b ) (a,b) ( a , b ) ( c , d ) (c,d) ( c , d )
4: Definition
만약 X = ( x 1 , ⋯ , x n ) X=(x_1,\cdots, x_n) X = ( x 1 , ⋯ , x n ) Y = ( y 1 , ⋯ , y n ) Y=(y_1, \cdots, y_n) Y = ( y 1 , ⋯ , y n ) E n E^n E n X X X Y Y Y
d ( X , Y ) = ( x 1 − y 1 ) 2 + ( x 2 − y 2 ) 2 + ⋯ + ( x n − y n ) 2 d(X,Y)=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2+\cdots+(x_n-y_n)^2} d ( X , Y ) = ( x 1 − y 1 ) 2 + ( x 2 − y 2 ) 2 + ⋯ + ( x n − y n ) 2 여기서 중요한 점은 X ≠ Y X\neq Y X = Y d ( X , Y ) > 0 d(X,Y)>0 d ( X , Y ) > 0 d ( X , X ) = 0 d(X,X)=0 d ( X , X ) = 0 d ( X , Y ) = d ( Y , X ) d(X,Y) = d(Y,X) d ( X , Y ) = d ( Y , X )
5: Definition
만약 X = ( x 1 , ⋯ , x n ) X=(x_1,\cdots, x_n) X = ( x 1 , ⋯ , x n ) Y = ( y 1 , ⋯ , y n ) Y=(y_1, \cdots, y_n) Y = ( y 1 , ⋯ , y n ) E n E^n E n
< X , Y > = x 1 y 1 + x 2 y 2 + ⋯ + x n y n <X,Y> = x_1y_1 + x_2y_2 + \cdots + x_ny_n < X , Y > = x 1 y 1 + x 2 y 2 + ⋯ + x n y n 6: Proposition
inner product는 다음과 같은 성질을 가진다.< X , Y > = < Y , X > <X,Y> = <Y,X> < X , Y > = < Y , X > < X , θ > = 0 , θ = ( 0 , ⋯ , 0 ) <X,\theta>=0,\quad \theta = (0, \cdots, 0) < X , θ > = 0 , θ = ( 0 , ⋯ , 0 ) < X , Y + Z > = < X , Y > + < X , Z > <X, Y+Z> = <X, Y> + <X, Z> < X , Y + Z > = < X , Y > + < X , Z > α < X , Y > = < α X , Y > = < X , α Y > \alpha<X,Y> = <\alpha X, Y> = <X, \alpha Y> α < X , Y > = < α X , Y > = < X , α Y > ( 1 , 2 , 3 ) (1,2,3) ( 1 , 2 , 3 ) ( − 2 , 5 , 0 ) (-2,5,0) ( − 2 , 5 , 0 ) E n E^n E n
< ( 1 , 2 , 3 ) , ( − 2 , 5 , 0 ) > = − 2 + 10 + 0 = 8 <(1,2,3),(-2,5,0)> = -2+10+0 = 8 < ( 1 , 2 , 3 ) , ( − 2 , 5 , 0 ) > = − 2 + 1 0 + 0 = 8 이다.< X , Y > = 0 <X,Y>=0 < X , Y > = 0 X X X Y Y Y
7: Proposition
모든 X , Y ∈ E n X, Y \in E^n X , Y ∈ E n
< X , Y > ≤ ( < X , X > ) ( < Y , Y > ) <X,Y>\leq (\sqrt{<X,X>})(\sqrt{<Y,Y>}) < X , Y > ≤ ( < X , X > ) ( < Y , Y > ) 여기서 < X , X > = ( d ( X , θ ) ) 2 ≥ 0 <X,X>=(d(X,\theta))^2 \geq 0 < X , X > = ( d ( X , θ ) ) 2 ≥ 0
8: Proposition
우리는 ∥ X ∥ = d ( X , θ ) \lVert X \rVert=d(X,\theta) ∥ X ∥ = d ( X , θ ) X X X
∥ X + Y ∥ ≤ ∥ X ∥ + ∥ Y ∥ \lVert X+Y\rVert \leq \lVert X \rVert + \lVert Y \rVert ∥ X + Y ∥ ≤ ∥ X ∥ + ∥ Y ∥ 이다.
8: Proof
∥ X + Y ∥ 2 = d ( X + Y , θ ) 2 = < X + Y , X + Y > = < X , X > + 2 < X , Y > + < Y , Y > = ∥ X ∥ 2 + ∥ Y ∥ 2 + 2 < X , Y > = ( ∥ X ∥ + ∥ Y ∥ ) 2 − 2 ∥ X ∥ ∥ Y ∥ + 2 < X , Y > ≤ ( ∥ X ∥ + ∥ Y ∥ ) 2 ( ∵ < X , Y > ≤ ∥ X ∥ ∥ Y ∥ i n 7 : p r o p o s i t i o n ) \begin{aligned} \lVert X + Y\rVert ^2 &= d(X+Y, \theta)^2 \\&=<X+Y,X+Y> \\&= <X,X> + 2<X,Y> + <Y,Y> \\&=\lVert X \rVert^2 + \lVert Y \rVert^2 + 2<X,Y> \\&= (\lVert X \rVert + \lVert Y \rVert)^2 - 2 \lVert X \rVert \lVert Y \rVert+ 2<X,Y> \\& \leq (\lVert X \rVert + \lVert Y \rVert)^2 (\because <X,Y> \leq \lVert X\rVert\lVert Y\rVert\quad in \quad 7: proposition) \end{aligned} ∥ X + Y ∥ 2 = d ( X + Y , θ ) 2 = < X + Y , X + Y > = < X , X > + 2 < X , Y > + < Y , Y > = ∥ X ∥ 2 + ∥ Y ∥ 2 + 2 < X , Y > = ( ∥ X ∥ + ∥ Y ∥ ) 2 − 2 ∥ X ∥ ∥ Y ∥ + 2 < X , Y > ≤ ( ∥ X ∥ + ∥ Y ∥ ) 2 ( ∵ < X , Y > ≤ ∥ X ∥ ∥ Y ∥ i n 7 : p r o p o s i t i o n ) 9: Corollary
d ( X , Y ) ≤ d < X , Z > + d < Z , Y > ∀ X , Y , Z ∈ E n d(X,Y) \leq d<X,Z> + d<Z,Y> \forall X,Y,Z \in E^n d ( X , Y ) ≤ d < X , Z > + d < Z , Y > ∀ X , Y , Z ∈ E n 9: Proof
먼저 한 가지 사실을 알고 가야 한다.
d ( X , Y ) = ( y 1 − x 1 ) 2 + ( y 2 − x 2 ) 2 + ⋯ ( y n − x n ) 2 = d ( θ , X − Y ) = ∥ X − Y ∥ ( ∵ 8 : P r o p o s i t i o n ) \begin{aligned} d(X,Y) &= \sqrt{(y_1-x_1)^2+(y_2-x_2)^2+\cdots (y_n-x_n)^2} \\&=d(\theta,X-Y) \\&=\lVert X-Y \rVert (\because 8: Proposition) \end{aligned} d ( X , Y ) = ( y 1 − x 1 ) 2 + ( y 2 − x 2 ) 2 + ⋯ ( y n − x n ) 2 = d ( θ , X − Y ) = ∥ X − Y ∥ ( ∵ 8 : P r o p o s i t i o n ) d ( X , Y ) = ∥ X − Y ∥ d(X,Y) = \lVert X-Y \rVert d ( X , Y ) = ∥ X − Y ∥ d ( X , Y ) = ∥ X − Y ∥ = ∥ X − Z + Z − Y ∥ ≤ ∥ X − Z ∥ + ∥ Z − Y ∥ = d ( X , Z ) + d ( Z , Y ) \begin{aligned} d(X,Y) &= \lVert X-Y \rVert \\&=\lVert X-Z + Z -Y \rVert \\&\leq \lVert X-Z \rVert + \lVert Z-Y \rVert \\&=d(X,Z) + d(Z, Y) \end{aligned} d ( X , Y ) = ∥ X − Y ∥ = ∥ X − Z + Z − Y ∥ ≤ ∥ X − Z ∥ + ∥ Z − Y ∥ = d ( X , Z ) + d ( Z , Y ) 10: Definition
집합 X X X X X X
d : X × X → R ≥ 0 d: X \times X \rightarrow \mathbb{R}_{\geq0} d : X × X → R ≥ 0 M1) d ( x , y ) = 0 ⟺ x = y d(x,y) = 0 \iff x=y d ( x , y ) = 0 ⟺ x = y d ( x , y ) = d ( y , x ) d(x,y)=d(y,x) d ( x , y ) = d ( y , x ) d ( x , y ) ≤ d ( x , z ) + d ( z , y ) d(x,y)\leq d(x,z)+d(z,y) d ( x , y ) ≤ d ( x , z ) + d ( z , y ) d d d X X X ( X , d ) (X,d) ( X , d ) X X X X X X n n n
10.1: Example (Euclidean metric)
R n \mathbb{R}^n R n
d ( x , y ) = ∑ i = 1 n ( x i − y i ) 2 , x = ( x 1 , x 2 , ⋯ , x n ) , y = ( y 1 , y 2 , ⋯ , y n ) d(x,y) = \sqrt{\sum_{i=1}^{n} (x_i-y_i)^2},\quad x=(x_1, x_2, \cdots, x_n),y=(y_1, y_2, \cdots, y_n) d ( x , y ) = i = 1 ∑ n ( x i − y i ) 2 , x = ( x 1 , x 2 , ⋯ , x n ) , y = ( y 1 , y 2 , ⋯ , y n ) (*4번에서 정의한 E n E^n E n L 2 L_2 L 2
10.2: Example (manhattan metric)
R n \mathbb{R}^n R n
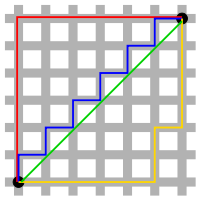
d 1 ( x , y ) = ∑ i = 1 n ∣ x i − y i ∣ , x = ( x 1 , x 2 , ⋯ , x n ) , y = ( y 1 , y 2 , ⋯ , y n ) d_1(x,y) = \sum_{i=1}^{n} \lvert x_i-y_i\rvert,\quad x=(x_1, x_2, \cdots, x_n),y=(y_1, y_2, \cdots, y_n) d 1 ( x , y ) = i = 1 ∑ n ∣ x i − y i ∣ , x = ( x 1 , x 2 , ⋯ , x n ) , y = ( y 1 , y 2 , ⋯ , y n ) L 1 L_1 L 1
10.3: Example
R n \mathbb{R}^n R n p > 0 p>0 p > 0
d p ( x , y ) = ∑ i = 1 n ( x i − y i ) p p , x = ( x 1 , ⋯ , x n ) , y = ( y 1 , ⋯ , y n ) d_p(x,y) = \sqrt[p]{\sum_{i=1}^{n} (x_i-y_i)^p}, \quad x=(x_1, \cdots, x_n), y=(y_1, \cdots, y_n) d p ( x , y ) = p i = 1 ∑ n ( x i − y i ) p , x = ( x 1 , ⋯ , x n ) , y = ( y 1 , ⋯ , y n ) 앞서 유클리드 거리와 맨하탄 거리를 이제부터 설명할 새로운 거리 정의로 표현할 수 있다.d 2 ( x , y ) = ∑ i = 1 n ( x i − y i ) 2 , x = ( x 1 , ⋯ , x n ) , y = ( y 1 , ⋯ , y n ) d_2(x,y)=\sqrt{\sum_{i=1}^{n} (x_i-y_i)^2}, \quad x=(x_1, \cdots, x_n), y=(y_1, \cdots, y_n) d 2 ( x , y ) = ∑ i = 1 n ( x i − y i ) 2 , x = ( x 1 , ⋯ , x n ) , y = ( y 1 , ⋯ , y n ) d 1 ( x , y ) = ∑ i = 1 n ∣ x i − y i ∣ , x = ( x 1 , ⋯ , x n ) , y = ( y 1 , ⋯ , y n ) d_1(x,y) = \sum_{i=1}^{n}\lvert x_i-y_i\rvert, \quad x=(x_1, \cdots, x_n), y=(y_1, \cdots, y_n) d 1 ( x , y ) = ∑ i = 1 n ∣ x i − y i ∣ , x = ( x 1 , ⋯ , x n ) , y = ( y 1 , ⋯ , y n )
10.4: Example (supremum metric)
R n \mathbb{R}^n R n
d ∞ ( x , y ) = max i = 1 , ⋯ , n ( ∣ x i − y i ∣ ) x = ( x 1 , ⋯ , x n ) , y = ( y 1 , ⋯ , y n ) d_\infty(x,y)=\max_{i=1,\cdots,n}(\lvert x_i - y_i \rvert) \quad x=(x_1, \cdots, x_n), y=(y_1, \cdots, y_n) d ∞ ( x , y ) = i = 1 , ⋯ , n max ( ∣ x i − y i ∣ ) x = ( x 1 , ⋯ , x n ) , y = ( y 1 , ⋯ , y n ) 이 또한 p = ∞ p=\infty p = ∞
10.5: Definition
R n \mathbb{R}^n R n d p d_p d p
d p ( α x , α y ) = ∣ α ⋅ d p ( x , y ) ∣ , d p ( x + z , y + z ) = d p ( x , y ) d_p(\alpha x, \alpha y) = \lvert \alpha \cdot d_p(x,y) \rvert , \quad d_p(x+z,y+z) = d_p(x,y) d p ( α x , α y ) = ∣ α ⋅ d p ( x , y ) ∣ , d p ( x + z , y + z ) = d p ( x , y ) 이런 성질로부터 벡터 x의 크기를 재는 함수 norm을 정의 할 수 있다.
∥ x ∥ = d p ( x , 0 ) \lVert x \rVert =d_p(x,0) ∥ x ∥ = d p ( x , 0 ) (*8: Proposition에서 정의한 ∥ X ∥ = d ( X , θ ) \lVert X \rVert=d(X,\theta) ∥ X ∥ = d ( X , θ ) ∥ x ∥ = 0 ⟺ x = 0 \lVert x \rVert = 0 \iff x=0 ∥ x ∥ = 0 ⟺ x = 0 ∥ α x ∥ = α ∥ x ∥ \lVert \alpha x \rVert = \alpha \lVert x \rVert ∥ α x ∥ = α ∥ x ∥ ∥ x + y ∥ ≤ ∥ x ∥ + ∥ y ∥ \lVert x+y \rVert \leq \lVert x \rVert + \lVert y \rVert ∥ x + y ∥ ≤ ∥ x ∥ + ∥ y ∥
10.6: Example
C [ 0 , 1 ] C[0,1] C [ 0 , 1 ] [ 0 , 1 ] [0,1] [ 0 , 1 ] C [ 0 , 1 ] : = { f : [ 0 , 1 ] → R ∣ f : c o n t i n u o u − f u n c t i o n } C[0,1] := \{f: [0,1] \rightarrow \mathbb{R} \quad \vert \quad f: continuou- function\} C [ 0 , 1 ] : = { f : [ 0 , 1 ] → R ∣ f : c o n t i n u o u − f u n c t i o n }
d p ( f , g ) : = ∫ 0 1 ∣ f ( x ) − g ( x ) ∣ d x , d ∞ ( f , g ) : = max x ∈ [ 0 , 1 ] ∣ f ( x ) − g ( x ) ∣ d_p(f,g):=\int_0^1 \lvert f(x)-g(x) \rvert dx, \qquad d_\infty(f,g):=\max_{x \in [0,1]}\lvert f(x)-g(x)\rvert d p ( f , g ) : = ∫ 0 1 ∣ f ( x ) − g ( x ) ∣ d x , d ∞ ( f , g ) : = x ∈ [ 0 , 1 ] max ∣ f ( x ) − g ( x ) ∣ 는 모든 양수 p > 0 p>0 p > 0
∥ f ∥ p = d p ( f , 0 ) \lVert f \rVert_p = d_p(f,0) ∥ f ∥ p = d p ( f , 0 ) 는 norm의 성질을 만족한다.L p L_p L p
10.7: Example (discrete metric)
임의의 집합 X X X
d ( x , y ) = { 0 x = y 1 x ≠ y d(x,y) = \begin{cases} 0 & \quad x=y\\ 1 & \quad x \neq y \end{cases} d ( x , y ) = { 0 1 x = y x = y Reference
D. W. Kahn, Topology: An Introduction to the Point-set and Algebraic Areas. Dover Books on Mathematics, 1995, p15-20 이종규, 위상수학. 북스힐, 2020, p146-151