1: Definition

Metric Space $(X,d)$위의 한 점 $x$와 양의 실수 $r>0$에 대해, open ball을 다음과 같이 정의한다.

점 $x$을 중심으로 반지름이 $r$인 모든 점들의 집합을 의미한다. $d(x,y) <r$이기 때문에 경계는 포함하지 않는다.

1.1: Example ($\mathbb{R}$에서의 open ball)

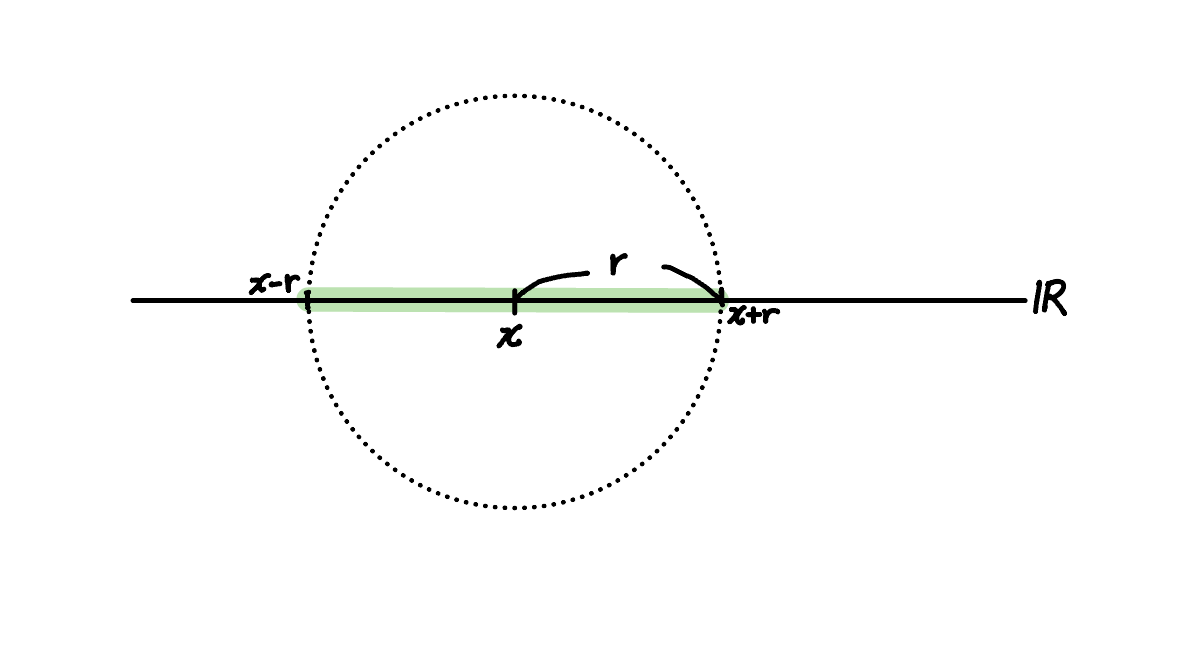
$\mathbb{R}$에서는 모든 $p>0$에 대해 $d_p(x,y) = \lvert x-y \rvert$이다.
이때 $B_r(x) = (x-r,x+r)$이다.

1.2: Example ($\mathbb{R}^3$에서의 open ball)

$\mathbb{R}^3$에서, 유클리드 거리($L_2$)로 정의되는 open ball은 일반적인 구의 형태와 동일하다.
다음은 원점(0,0,0)을 기준으로 반지름이 1인 open unit ball이다.

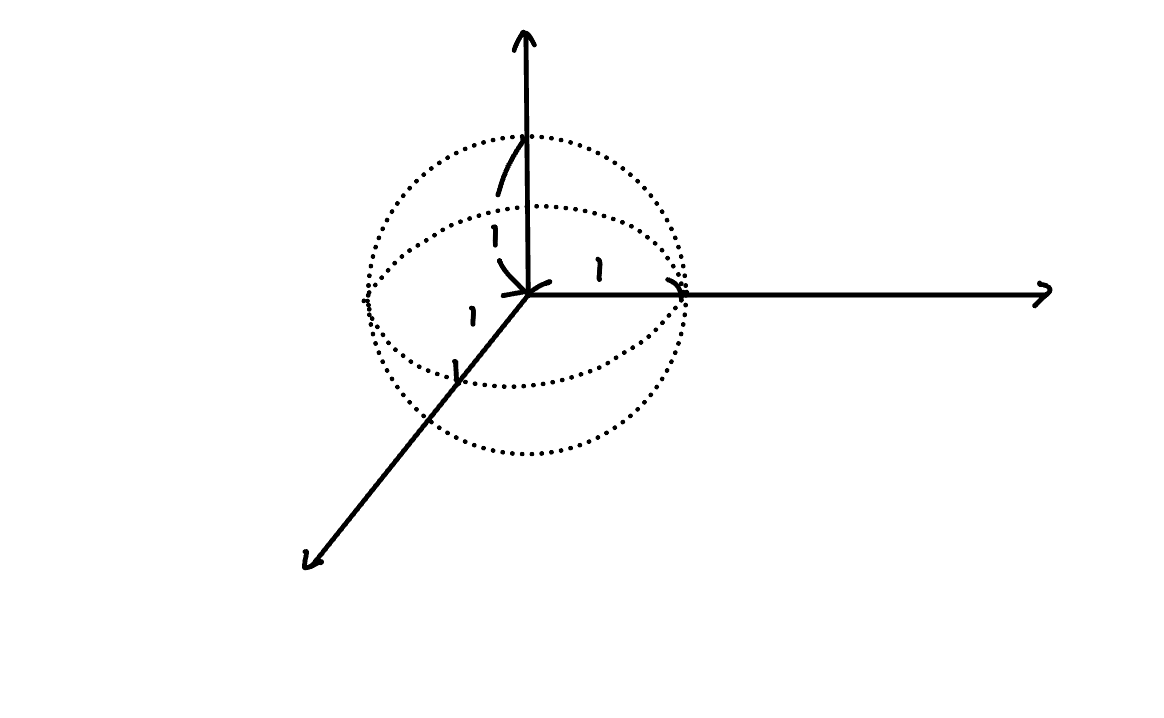
open ball의 내부는 '경계를 제외하고' 전부 채워져있다는 사실을 인지해야한다

1.3: Example ($\mathbb{R}^2$에서의 open ball)

$\mathbb{R}^2$ 에서, 맨하탄거리($L_1$)로 정의된 open ball은 rhombus(마름모)모양이다.

$\mathbb{R}^2$ 에서, 유클리드거리($L_2$)로 정의된 open ball은 다음과 같다.

$\mathbb{R}^2$ 에서, $d_\infty(x,y)$(supremum metric)로 정의된 open ball은 정사각형 모양이다.

1.4: Example (Discrete metric과 open ball)

먼저 Discrete metric에 대한 정의를 다시 상기하자.
Discrete metric에서 open ball은 두가지 경우로 나눌 수 있다.

1. radius가 1보다 크면 open ball의 정의(1:Definition)에 따라 0 또는 1로 결정된다.

open ball의 정의:

여기서 $d(x,y)$는 Discrete metric에 따라 $x=y$이면 $d(x,y) = 0$이고, $x \neq y$이면 $d(x,y) = 1$이다.
따라서 전체 집합$X$에 있는 모든 점에 대해서 중심이 $x$인 $d(x,y)$는 $1$과 $0$말곤 나올 수 없다. ($B_r(x)$에 포함될 수 있는 조건 $d(x,y)<r$를 $y \in X$인 모든 점이 만족한다.)
따라서 $B_r(x) = X$이다.
2. radius가 1보다 작거나 같으면, open ball의 정의에서 문제가 생긴다.
$d(x,t) < r$을 만족하는 전체 집합 $X$에 있는 점은 open ball의 중심인 $x$ 자기 자신 밖에 존재하지 않는다.
따라서 $B_r(x) = \{x\}$이다.

1.4.1: Remark (Discrete metric)

임의의 집합 $X$에서 다음과 같이 정의된 discrete metric도 거리의 정의를 만족한다.

2: Definition

Metric space$(X,d)$안의 임의의 open ball $B_r(x)$에서 임의의 원소 $y \in B_r(x)$에 대해, 다음을 만족하는 $\delta>0$가 존재한다.

2: Proof

$s=d(x,y)$라고 하자. 이 값은 무조건 $r$보다 작다.($\because B_r(x)$는 open ball)
$\delta>0$를 다음과 같이 만들 수 있다.

이렇게만 $\delta$를 규정해야하는 것은 아니지만, $\delta$가 위와 같이 정의되어 있을때가 가장 보편성을 띈다. 그 이유는 다음 과정에서 설명된다.
이렇게 규정할 수 있는 이유는 아래 그림을 통해서 알 수 있다.

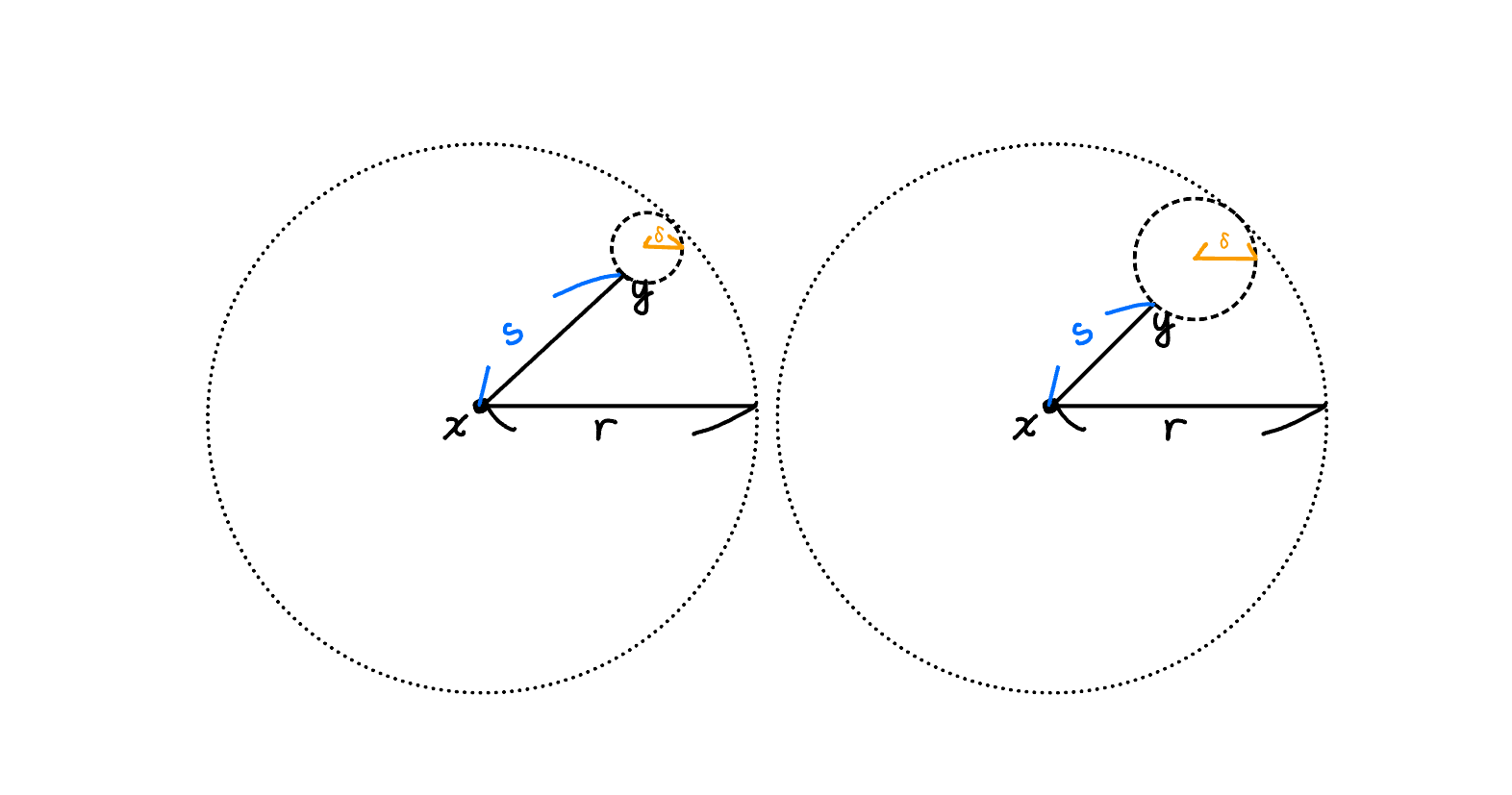
$B_\delta(y) \subset B_r(x)$를 증명하는 가장 보편적인 방법은 open ball $B_\delta(y)$에 포함된 임의의 원소$z$가 $B_r(x)$에 들어간다를 보이는 것이다.

$z\in B_\delta(y) \subset B_r(x)$를 보이기 위해 triangle inequality를 사용한다.

$d(z,x)<r$이라는 사실은 $z\in B_r(x)$라는 사실을 보여준다.

2.1: Example ($\mathbb{R}^2$에서 openball 안의 open ball)

앞서 살펴본 open ball in an open ball은 유클리드 거리($L_2$)를 바탕으로 정의한 것이다.
유클리드 거리가 아닌 다른 거리($d_1$, $d_\infty$)에서도 정의할 수 있다.

2.2: Corollary

Metric space $(X,d)$ 안의 두 open ball $B_r(x)$, $B_s(y)$가 있을 때,$z\in B_r(x), B_s(y)$인 $z$가 존재한다고 하자.
그러면, 다음 조건을 만족하는 $\delta>0$를 찾을 수 있다.

위 상황은 아래와 같은 그림으로 표현할 수 있다.

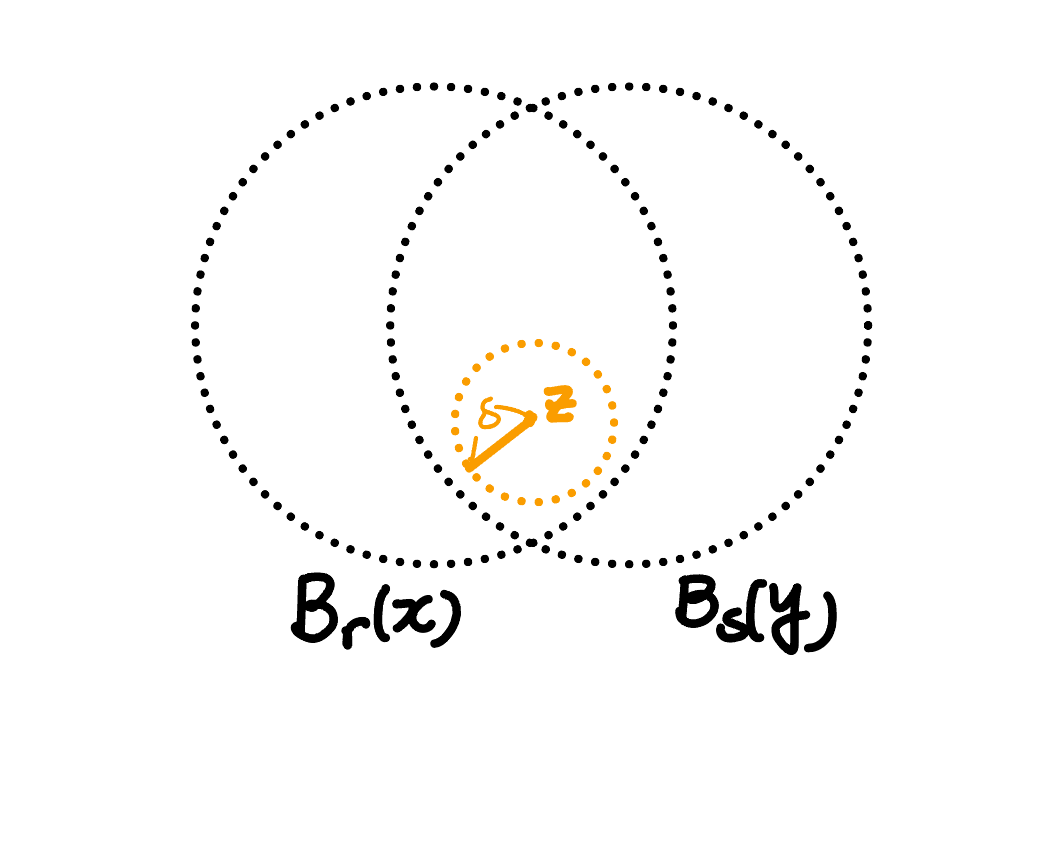
2.2: Proof

두개의 open ball을 분리해서 접근하는 것이 좋다.
2: Definition에 따르면 $B_{\delta_{1}}(z) \subset B_r(x)$인 $B_{\delta_{1}}(z)$를 정의할 수 있다.
2: Definition에 따르면 $B_{\delta_{2}}(z) \subset B_s(y)$인 $B_{\delta_{2}}(z)$를 정의할 수 있다.
여기서 핵심이 되는 아이디어는 $\delta$를 $\min(\delta_1, \delta_2)$으로 생각하는 것이다.
위 세문장을 전부 합쳐서 보면

를 만족한다. 따라서 $B_\delta(z) \subset B_r(x) \cap B_s(y)$이다.

3: Definition

Metric Space $(X,d)$위의 한 점 $x$와 양의 실수 $r>0$에 대해, closed ball을 다음과 같이 정의한다.

4: Definition

앞서 살펴본 open ball과 closed ball을 $E^n$으로 확장할 수 있다.
$E^n$에서의 open $n$-ball은

$E^n$에서의 closed $n$-ball은

이다.

5: Definition

$(n-1)$-sphere는 다음과 같이 정의한다.

즉, $S_r^{n-1}(x)$는 $\{y\in E^n \vert d(x,y) = r\}$이라는 뜻이다.
여기서 핵심은 ball은 $n$-dimension이고, sphere는 $n-1$-dimension이라는 사실이다.

Reference

D. W. Kahn, Topology: An Introduction to the Point-set and Algebraic Areas. Dover Books on Mathematics, 1995, p22-23
이종규, 위상수학. 북스힐, 2020, p152-155