😀우리가 일상생활에서 나이맞추기 퀴즈? 같은 것을 하거나 주변인과 소통을 하면서 특정 수에 대해서 나는 결과를 알고있고, 상대방이 못 맞췄을 때 힌트를 주기위해서 up & down으로 특정 수를 찾을 수 있게 도와준 경험이나, 이야기를 들어보았을 것이다.
예를들어, 필자의 나이는 32살이지만, 상대방이 나이를 물었을 때 맞춰보라고 하고 40이라 대답하면 나는 down이라는 힌트를 주고
상대는 40의 아랫값에서 또 내 나이를 유추할 것이다. 이러한 숫자 유추에서 효율적인 방법이 중간점 탐색을 이용한 소거 방식이다.
이런 중간점 탐색방식이 이진탐색이다. 아무래도 절반식 소거해 나가는 쪽이 더 많은 예외를 제외할 수 있게 될 것이다.
이러한 이진탐색에 대해서 알아보도록 하자.
이진탐색이란?
이진 탐색이란 정렬돼 있는 데이터에서 특정한 값을 찾아내는 알고리즘이다.
-
이진탐색은 이분탐색이라고도 불린다. 이진탐색은 탐색 범위를 반으로 나누어 찾는 값을 포함하는 범위를 좁혀가는 방식으로 동작한다. 주로 배열의 인덱스를 기준으로 배열 내의 값을 탐색하는데 사용되지만, 리스트, 트리 등에서도 사용할 수 있다.
-
❌하지만 모든 리스트, 트리에서 사용할 수 있는 것이 아니라 반드시 원소들이 일정한 순서(예를 들면 오름차순)로 정렬된 구조에서만 사용할 수 있기 때문에 정렬된 리스트나 트리에서 사용이 가능하다.
-
이진탐색의 시간 복잡도는 O(log n)으로, 배열의 크기에 비례하여 실행 시간이 빨라진다.
따라서 대용량 데이터에서 특정 값의 위치를 찾는 데 용이하다.
이진탐색의 동작 방식
😀이진 탐색의 동작 방식은 우리가 생각하는 중간점 탐색소거 방식과 크게 다르지 않다.
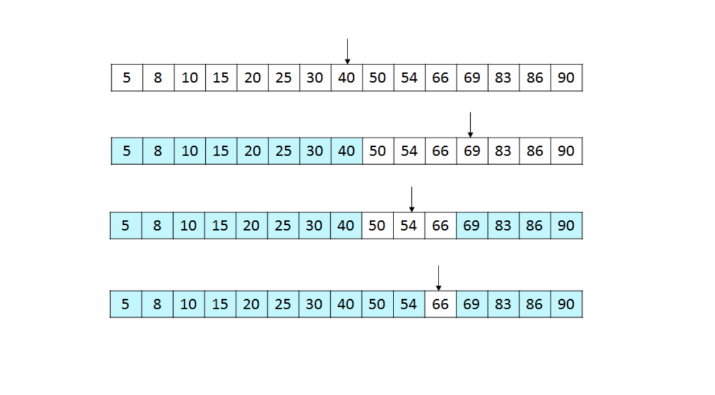
배열에서의 동작방식
- 정렬된 배열에서 중간 인덱스(mid)를 찾는다.
- 찾으려는 값(target)과 중간 값(mid_val)을 비교한다.
- target이 mid_val보다 작으면 mid를 기준으로 왼쪽 부분 배열을 탐색한다.
target이 mid_val보다 크면 mid를 기준으로 오른쪽 부분 배열을 탐색한다. - 탐색 범위를 반으로 줄인다.
- 탐색 범위가 더 이상 없을 때까지 위 과정을 반복한다.
function binarySearch(arr, target) {
let left = 0;
let right = arr.length - 1;
while (left <= right) {
let mid = Math.floor((left + right) / 2);
if (arr[mid] == target) {
return mid;
} else if (arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1;
}
const arr = [1, 2, 3, 4, 5, 6];
const target = 3;
const index = binarySearch(arr, target);
console.log(index); // 2위 코드의 binarySearch 함수는 탐색 범위의 왼쪽 끝 인덱스(left)와 오른쪽 끝 인덱스(right)를 지정하고, 이진탐색을 반복문으로 사용하여 구현한다.
매 반복마다 중간 인덱스(mid)를 계산하여, 찾으려는 값과 중간 값과를 비교하여 탐색 범위를 줄인다.
만약 찾으려는 값과 중간 값이 일치하면 중간 인덱스를 반환하고, 일치하는 값이 없으면 -1을 반환한다.
트리에서의 동작방식
- 트리에서 중간 노드를 찾는다.
- 찾으려는 값과 중간 노드의 값과를 비교한다.
- 찾으려는 값이 중간 노드의 값보다 작으면 왼쪽 하위 트리에서 탐색을 계속한다.
찾으려는 값이 중간 노드의 값보다 크면 오른쪽 하위 트리에서 탐색을 계속한다. - 탐색 범위를 반으로 좁힌다.
- 탐색 범위가 더 이상 없을 때까지 위 과정을 반복한다.
⛔주의점❗❗
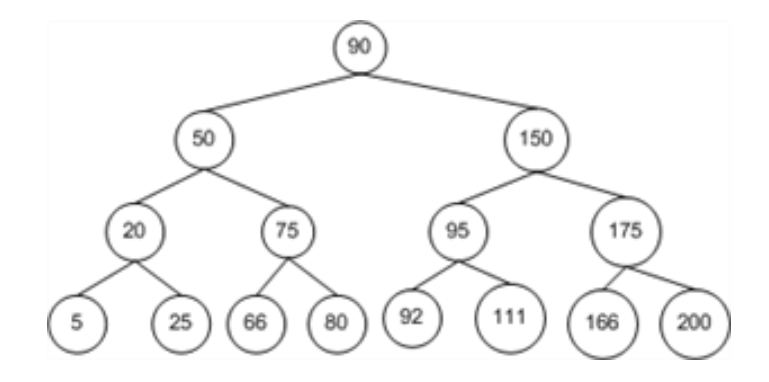
- 트리 구조에서 이진탐색을 적용하기 위해서는, 탐색 대상이 되는 트리가 반드시 이진탐색 트리(Binary Search Tree) 구조를 가져야 한다.
❓이진탐색 트리란?
- 각 노드가 하나의 키를 저장하고, 왼쪽 서브트리의 키는 부모 노드의 키보다 작고, 오른쪽 서브트리의 키는 부모 노드의 키보다 큰 이진트리의 형태이다.
이진탐색의 장단점
😀이진탐색은 검색속도에 대한 장점을 주로 보인다. 하지만 장점이 있다면 단점도 있기 마련이다.
장점
-
검색 속도가 빠르다.
검색 대상의 크기와 상관없이 빠른 검색 속도를 제공한다는 것으로, 검색 대상이 매우 큰 경우에도 탐색 시간이 빠르기 때문에, 대량의 데이터를 다루는 알고리즘에서 많이 사용된다. -
O(log n)의 검색 속도를 보장한다.
이진탐색은 검색 대상이 정렬되어 있다는 가정하에 이론적으로 최악의 경우에도 O(log n)의 검색 속도를 보장한다. 즉, 검색 대상의 크기가 커져도 검색 시간이 늘어나는 속도가 상대적으로 느리기 때문에 가능하다.
단점
-
반드시 특정구조가 필요하다.
가장 큰 단점은 배열이나 이진탐색 트리와 같이 정렬된 구조에서만 사용할 수 있다는 것이다.
만약 데이터가 정렬되어 있지 않은 경우에는 이진탐색을 사용할 수 없다. -
검색대상의 생성, 수정에 취약하다.
이진탐색은 탐색을 위해 추가적인 메모리를 사용하지 않기 때문에, 검색 대상을 계속해서 수정하거나 추가하는 경우에는 탐색 시간이 길어질 수 있다.
참고자료(출처)
어소락트 게임아카데미 자료구조 - 이진탐색트리
네이버블로그 BQRIUM 자료구조 이진 탐색(Binary search)
위드블록 유튜브 동영상 [검색] #2 이진검색 - 위드블록
깃허브io cjh5414 포스팅 이진 탐색(Binary Search) 알고리즘 개념 이해 및 추가 예제

===이라고 쓰셨습니다