241107
https://wlsdndml213.tistory.com/21
- 행만 뒤집기로 했다.
내 생각에는 1행이니까. 1행을 고정된 상태에서 해야 겠다는 생각으로 이렇게 함.
그런데 이거는 맞지 않다...
조건식에서 행에 대한 확인진행하지 않게 막아버린다.
- 이렇게 해야 한다는데 공부 필요.
최근 풀이 : 240126
-
행이랑 열을 전부 다 비트마스킹 처리하는 방식으로 함.
https://www.acmicpc.net/submit/1285/72413458 -
놓친 부분 : 그리디....
: 위의 코드는 행,렬 을 2개로 구분지어서 진행한 것임. -
위 코드에다가 코드를 추가하면 출력을 확인할 수 있음.
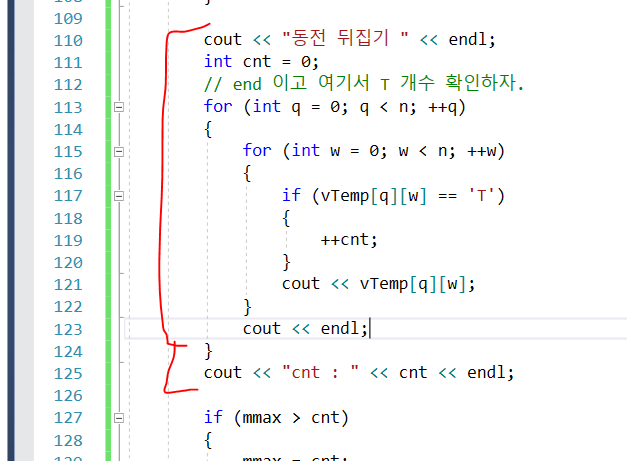
접근법.
- 문제를 풀 때, 시간복잡도 부터 확인해었어야 함.
n은 20이니까.
-> 지금 문제에서 한행을 통째로 돌리거나 한열을 통째로 돌리니까.
한행이나 한 열은 n 이고 즉 2의 n승 -> 2의 20승이다.
문제에서 한행 또는 한열 이므로 2의 20 승 * 2의 20승이다.
즉 2의 40승...
- 결론
: 시간 초과된다.
즉 가로 ,세로 전부 다 탐색을 하든 그 생각은 잘못되었다.
다른 방법을 생각해야 한다.
// 아래는 큰돌 강의 내용이고
n의 최대값은 20이고, 행과 열 모두 뒤집어야 하니까 , 2의 40승이라고 생각함...
-
2의 10승은 1024 이고, 1000 X 1000 X 1000 X 1000 은.... OMG...
100만 X 100만은 100 100 10000 10000 => 10000 10000 10000 : 100억이고?? -
시간 초과 : 6초니까 6억임.
-> 이미 시간 초과.
그래서 어떻게 할 건데
-
문제의 본질은 T를 최소한으로 만드는 문제임
-> 굳이 행,열 뒤집을 필요가 없음.
1열을 기준으로 해서 행만 뒤집는 방법을 생각해보자. -
행만 뒤집는 비트마스킹을 구하면 열을 뒤집을 필요 없이 최적해가 만들어진다.
-> 무슨 소리일까???
T
H
H
T
T
T
의 열이 정해져 있을 때, 다른 열에도 영향을 끼치겠지만. 가로행만 뒤집는 것으로만 열의 최적해를 구할 수 있다.
지금의 경우 1,4,5,6행을 뒤집으면 최고다!!!
핵심) 번거롭지만, 직접 작성해서 열을 뒤집을 필요 없는 이유를 생각해보자!!
- 행의 비트마스킹 , 모든 자릿수에 대한 경우의 수를 처리함으로써,
최적의 값을 구할수 있기 때문에, 열을 뒤집을 필요 없음!
- 1번) 1행만 뒤집으면
TTH
THH
THT
: 1열에서의 T의 개수는 : 3개
-> 1열의 입장에서 1열을 뒤집을까? 말까? 생각할 수있는 부분은
T의 갯수를 줄여야 하니까 지금은 뒤집어야 겠네??
-
2번) 2행만 뒤집으면
HHT
HTT
THT
: 1열에서의 T의 개수는 : 1개
-> 1열 입장에서는 최적의 조건은 안뒤집는게 좋겠네? -
3번) 3행만 뒤집으면
HHT
THH
HTH
: 1열에서의 T의 개수는 : 1
-> 1열 입장에서는 최적의 조건은 안뒤집는게 좋겠네? -
4번) 1행, 2행 뒤집으면
TTH
HTT
THT
: 1열에서의 T의 개수는 : 2
-> 1열 입장에서는 최적의 조건은 뒤집어야 겠네 -
5번) 1행, 3행 뒤집으면
TTH
THH
HTH
: 1열에서의 T의 개수는 : 2
-> 1열 입장에서는 최적의 조건은 뒤집어야 겠네 -
6번) 2행, 3행 뒤집으면
HHT
HTT
THT
: 1열에서의 T의 개수는 : 1
-> 1열 입장에서는 최적의 조건은 안뒤집는게 좋겠네? -
7번) 1,2,3 행 모두 뒤집으면
TTH
HTT
HTH
: 1열에서의 T의 개수는 : 1
-> 1열 입장에서는 최적의 조건은 안뒤집는게 좋겠네?
더 생각
: 2열의 입장에서도 생각해보면, 행 뒤집는 결과를 통해서 굳이
2열 뒤집는 연산을 안해도 최적의 조건이 나옴.
고찰
: 열이 뒤집거나 안뒤집는 비트마스킹 을 수행하지 않아도,
행의 비트마스킹 동작으로 인해서 최적의 조건
T의 개수 최소화 동작은 이미 결정된다는 것을 생각할 수 있음.
- 결론
: 열은 안뒤집어도 됨.
언제 품?
: 220912
https://www.acmicpc.net/source/49036626
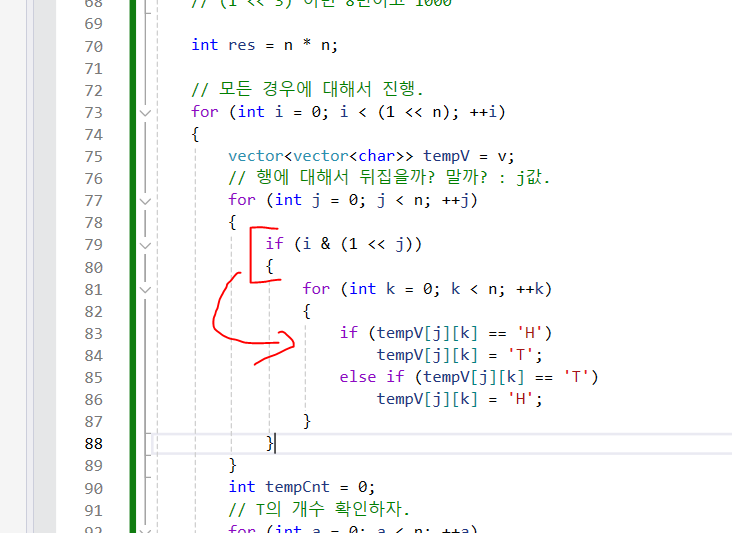
💎개선할 점.
1. 사고의 전환이 필요함
-
정상적으로 행순서로 확인을 하고 있는 부분임.
그런데 이렇게 하게 되면, 1행이 이루어진 후에 , 1열에 대해서 t와
h의 카운팅을 한다는 것인데, 여기서 어찌할 도리가 전혀 없음... -
그림 : 기본적으로 생각할 수 있는 행을 기준으로 해서 처리하는 그림.
-
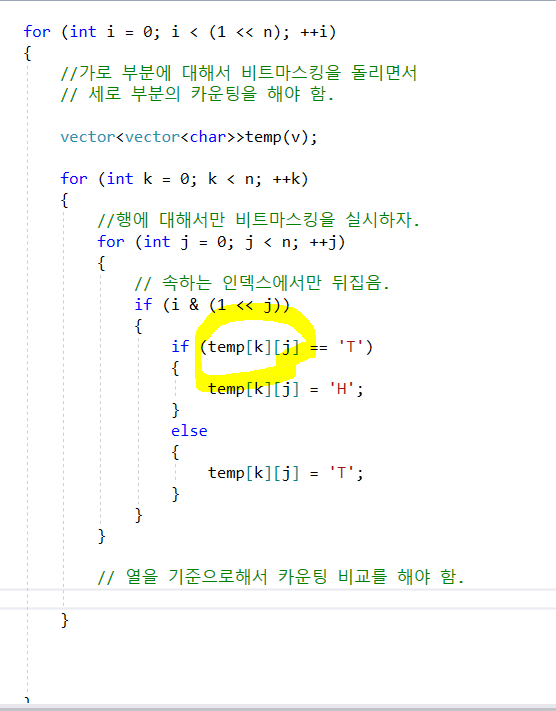
일단 비트마스킹을 하기 전에 염두해야 할 부분이 무엇인가를 생각해야 함.
: 고것은 바로 열에 위치한 원소간의 카운팅 비교임. -
내가 하고자 하는 것은 행에 대한 비트마스킹이 완료된 후에, 열에 대해 카운팅을 이루겠다는 것임.
예를 들어 0번째 열에 대해 카운팅을 하려면, [0][0] [1][0] [2][0]
원소들에 관해서 비트마스킹이 모두 이루어 져야 한다는 것임. -
결론 : 0번째 열 처리 하기 위해 열을 기준으로 해서 변경해야 함!
-
그림 : 열을 기준으로 해서 처리하고 있는 그림.
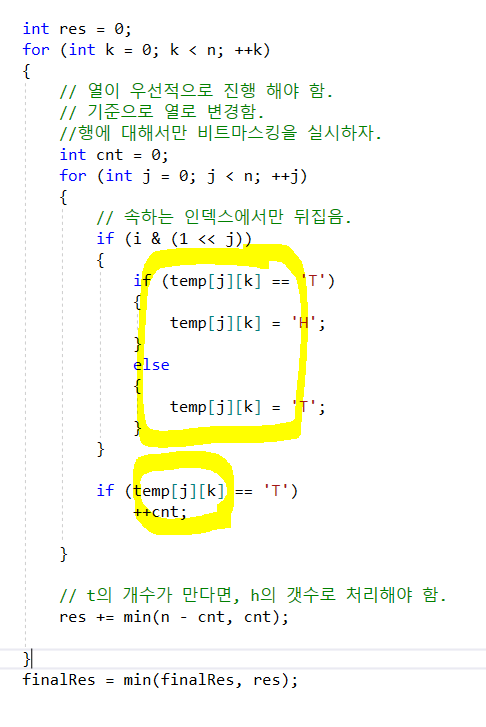
2. 작은 범위로 나누어서 진행하자.
- 내 생각에는 가로 행에 관한 모든 것을 변경한 다음에, 다시 또
열에 대해 카운팅 하는 방식임.행 한줄에 전체에 대해서 진행하는 것이 아니라,
각 원소를 가지고 확인하는 방식으로 진행하자.
최근 풀이
: 비트마스킹에 맞춰서 가로를 뒤집어 말어를 처리한 후에,
반복문을 한 번 더 써서 각 세로원소를 확인해 카운팅 하는 방식으로
접근함.
-> 틀림..
- 고찰
n번에 대한 연산을 추가적으로 한번 더 진행하고 있음.
// 세로의 원소를 빼면서, 그게 만약 가로에 속한 원소라면
// 비트마스킹을 처리하는 방식으로 진행하면 됨.
// => 어려움..
중요한 부분!_그리디 하게 접근하는 사고를 가지자!
- 출처 : 백준
: 한 행또는 한 열에 놓인 n개의 동적을 모두 뒤집는 작업을 수행할 수 있음.
-> 뒤집어도 되고, 안뒤집어도 된다를 의미함.
- 문제를 맨 처음에 접했을 때 나의 생각
1) 가로 로만 뒤집어?
2) 세로 로만 뒤집어?
3) 가로 세로 번갈아가면서 뒤집을 수 도 있겠네?
4) 가로 뒤집다가 세로뒤집다가 말고?
첫번째로 중요한 부분 : 시간 복잡도.
- 시간복잡도
-> 내가 생각한 최대의 경우의 수 위에서 3)번을 선택할 경우,
시간 복잡도는 2의 20승 * 2 번 => 2의 40승이다.
: 코드를 할 수 없는 지경임.
-
결과
: 가장 적게 나오는 t의 개수를 구하라. -
개선하는 생각을 해보면.
HTHTH
TTTTH
HHTTT
THTHT
HTTHH
일단 행을 뒤집기는 쉬우므로, 행을 뒤집어 말어?
생각을 할 수 있음.
그리고 나서,
열도 뒤집어 말어? 라는 진행을 할 수 있는데,
가 ) 1행을 뒤집으면
T
T
H
T
H
나) 1행을 뒤집지 않으면
H
T
H
T
H
여기서 굳이 열을 뒤집어? 말어 생각할 필요없이
행을 뒤집어 말어에 따라서 둘중에 하나는 최소의 갯수
t를 구할 수 있기 때문에
=> 열을 뒤집어 말어 생각할 필요가 없어짐
- 결론
: 시간 복잡도를 2의 20승으로 나타낼 수 있음.
알고리즘 분류
: 비트마스킹, 그리디
직접 풀이
- 나의 풀이법
20 20이므로 , 시간복잡도는 무관하지 않을까? 생각을 햇지만, 오산!
최대 2의 20승 2의 20승 으로 처리해야 하므로.
숫자가 많이 필요하다.
- 0906 화요일 : 구현하는데에 있어서 좀 비슷했음.
http://boj.kr/2376f5068ff342818a8639c34a715d58
-> 비슷하게 구현한듯한데, 99퍼센트가 부족함...
이해하기 어려운..
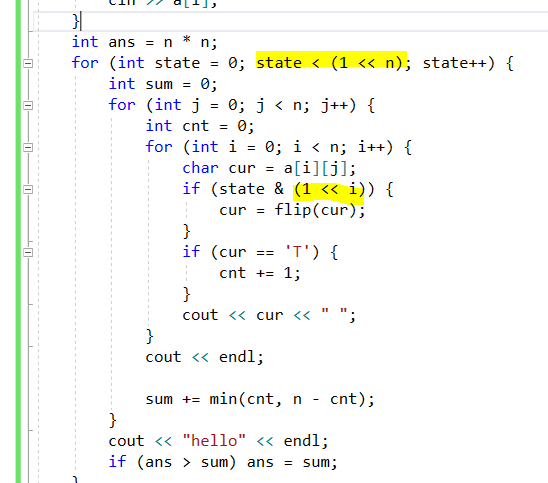
1) 첫번째 for문에서 행에 대한 경우의 수를 만들어 줬음.
2) 그리고 열에 대해서도 경우의 수를 처리를 해야함.
: 그 부분이 2번재 형광 부분...
따라서 좀 이상하게 열부터 증감을 한 후에, 행 증감이 이루어짐을
확인 할 수 있음.
분석 -> 비트마스킹
: 문제를 읽어보면, 뒤집으면 , 전체 행의 원소들의 값이
T -> H , H -> T로 변하게 됨.
2개의 값밖에 없으므로,
가) 0과 1을 사용하고,
나) ~ 연산자를 사용해야 겠다라는 생각을 하게 되었음.
첫번째 코드
- 가로만 뒤집어 나가는 코드
: 당연히 안됨...
#include <iostream>
#include <vector>
using namespace std;
#include <algorithm>
#include <queue>
#include <string>
int n;
void uReverse(vector<char>&v)
{
for (int i = 0; i < n; ++i)
{
if (v[i] == 'H')
v[i] = 'T';
else
v[i] = 'H';
}
}
// 3:24
int main()
{
cin >> n;
vector<vector<char>>v(n, vector<char>(n));
for (int i = 0; i < n; ++i)
{
string s;
cin >> s;
for (int j = 0; j < n; ++j)
{
v[i][j] = s[j];
}
}
//행만 뒤집어 말어를 결정하면 됨 .
// 만약에 행이 3개라고 하면
// 경우의 수는
// 1,2,3
int res = n * n;
for (int i = 0; i < (1 << n); ++i)
{
vector<vector<char>>v2(v);
int temp = 0;
for (int j = 0; j < n; ++j)
{
if (i & (1 << j))
{
cout << i << "번" << j << "뒤집어" << endl;
//해당되는 행을 뒤집어
// 한줄 씩만 들어옴.
uReverse(v2[j]);
// 원복을 해야 함.
}
cout << "output1" << endl;
for (int a = 0; a < n; ++a)
{
for (int b = 0; b < n; ++b)
{
cout << v2[a][b] << " ";
}
cout << endl;
}
cout << "output2 " << endl;
temp += count(v2[j].begin(), v2[j].end(), 'T');
}
// 끝나고 원복 해야함.
// 계산을 진행하자.
// t의 개수는?
res = min(res, temp);
}
cout << res << endl;
}
