최근 풀이 250604

• 풀이전략
  : 가정값을 얻어서 모든 파에 비교해서 카운트값을 얻는 것이다.

• 지금 상황에서 생각해보기.
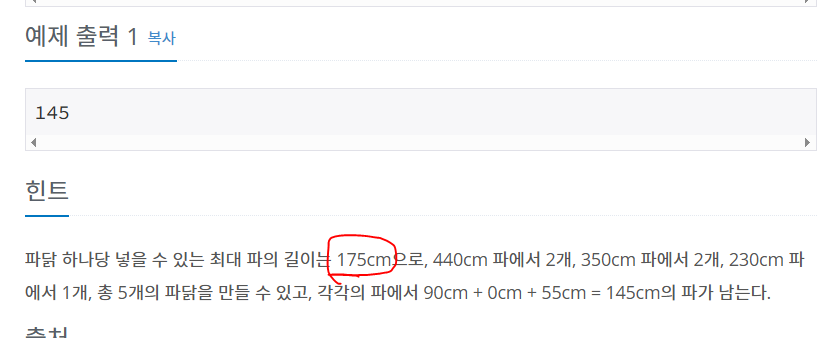
  : 타겟값으로 모든 파를 나누었더니 4가 되었다.
  과연 4는 true인가? 그렇지 않다. 문제에서는 주문받은 파닭의 수를 처리해야 한다고 한다.
  그렇다는 것은
  
  

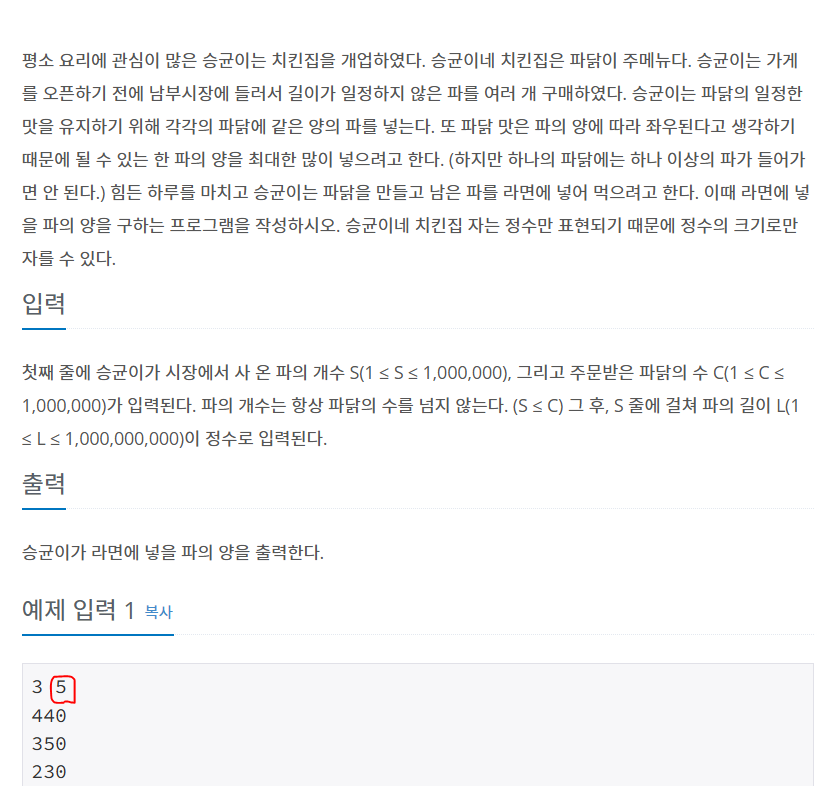
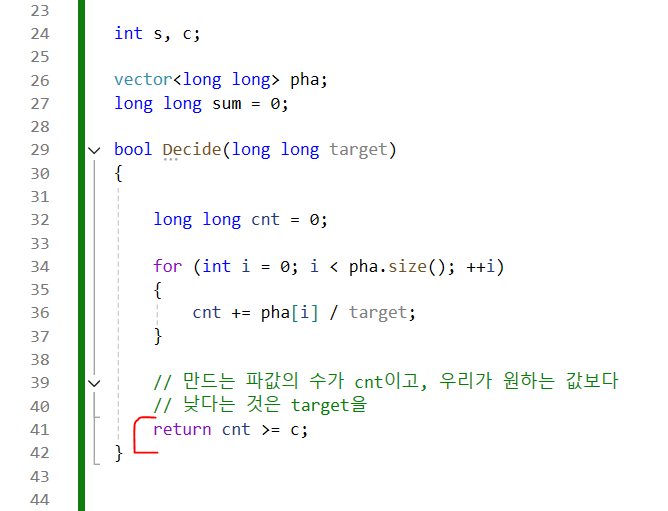
• Decide를 이렇게 작성해야 한다.
  : 구한 파닭의 개수가 넘어도 괜찮다.
  

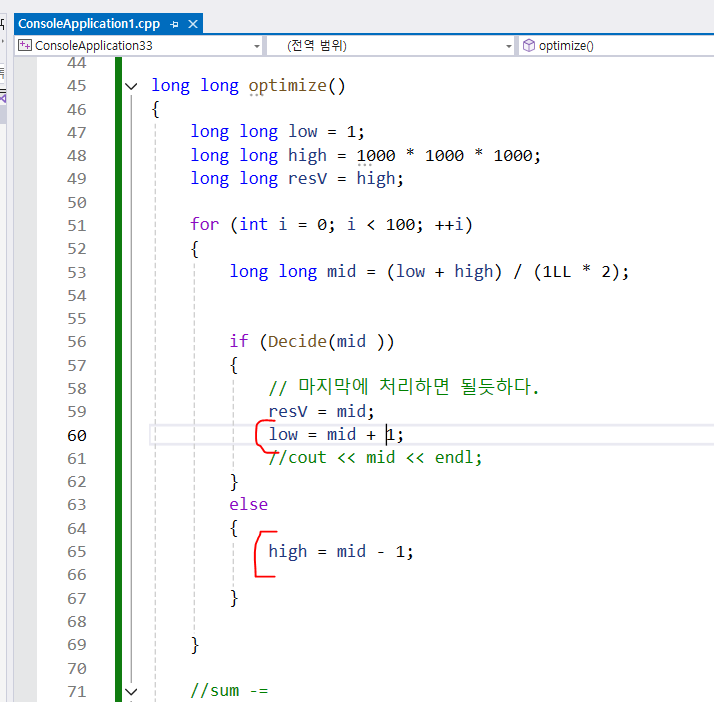
• 그러면 조건식 처리할때 최소값으로 처리하면 안된다.
  : 여기서는 최대한 c와 cnt가 동일하게 해야하므로,
  이렇게 하면 안된다.
  

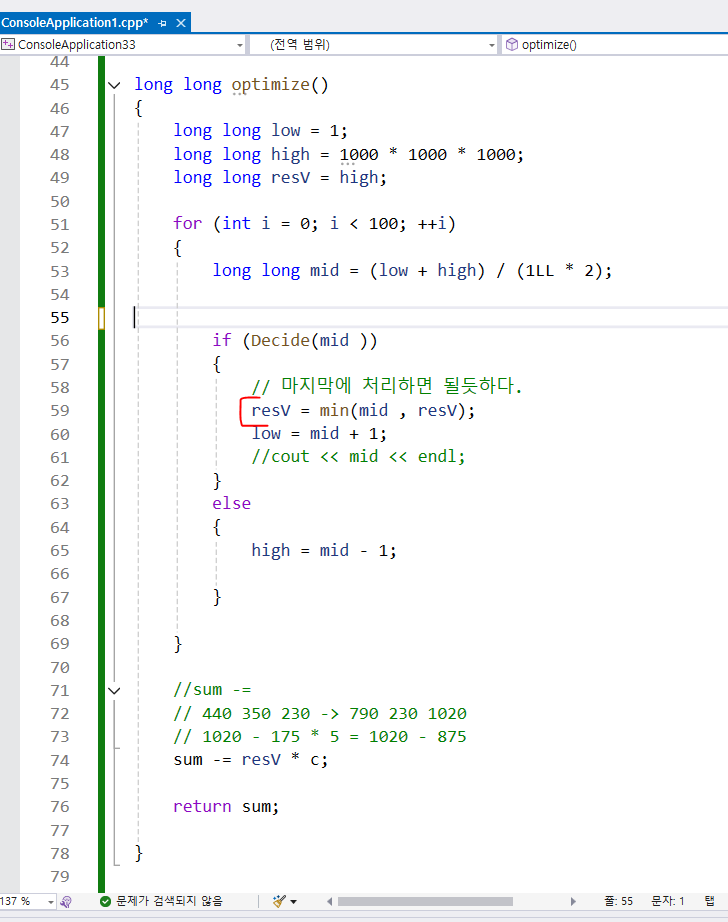
• 이렇게 최신갱신된 값을 넣어줘야 한다.
  

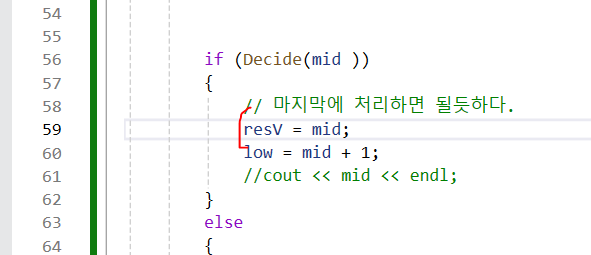
• 기존의 최적화 결정 문제에서는 그냥 mid값 대입했는데, 틀린다.
  

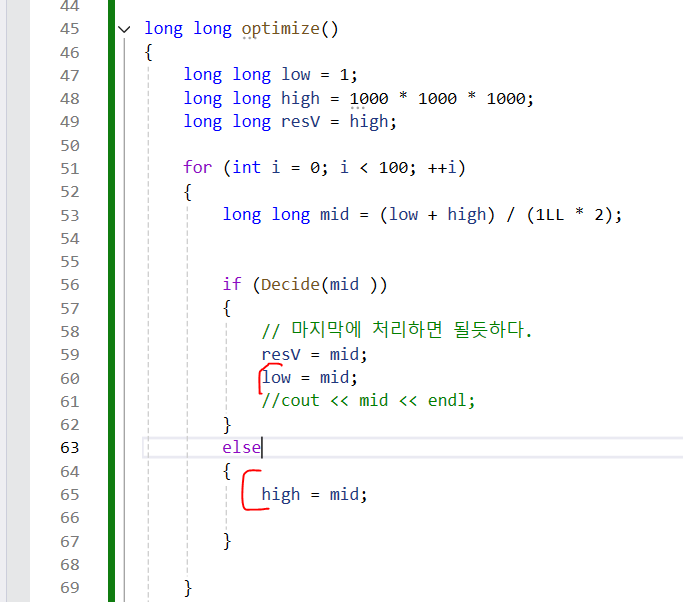
• 이렇게 해야 최종적인 답이다...