용어 정리_260414

• nPr : 순열 : 서로 다른 n개의 원소에서 r개를 뽑아 순서를 고려하면서 배치하는 것
  -> n! / (n - r)!

순열이므로, 1,2,3 과 3,2,1 은 다르다.

• nCr : 조합 : 서로 다른 n개의 원소를 r개 뽑아 순서 고려 없이 배치
  -> n! / (n - r)! * r!
  // 여기서 r! 을 나누는 것은 중복처리하는 거다.

조합이므로, 1,2,3과 3,2,1은 동일하다.
즉, 중복을 고려해야 한다.

---

경우의 수 설명.

1. 조합._260414

원리
: 중복처리가 되므로, 이미 앞에서 처리된 내용을 다시 확인하지 않으므로, 재귀함수에 인자로 idx 값이 필요하다.
그리고 앞으로 가서 확인하지 않기 때문에 bool값 필요 없다.

2. 순열_260414

원리
: 순서를 고려하는 것이므로, 다시 앞의 value를 참조하는 것이므로, go 함수에서 idx값 필요 없다.
앞의 idx로 가서 확인하는 것이고, 또 중복허용하지 않기 때문에 bool값 필요하다.

3. 중복 순열

원리.
: 중복 처리를 하지 않으면서 순서를 고려하면서 나열 하는 것이므로
앞선 value를 다시 참조하므로, go 함수에 idx 값 필요 하지 않다.

4. 중복 조합

원리
: 중복 처리를 하고 있고, 다음 원소가 다음에 오는 것이 아니라,
동일한 값이 연속으로 나올 수 있기 때문에 idx + 1을 건네 주지 말고, idx 를 건네자.

---

조합.

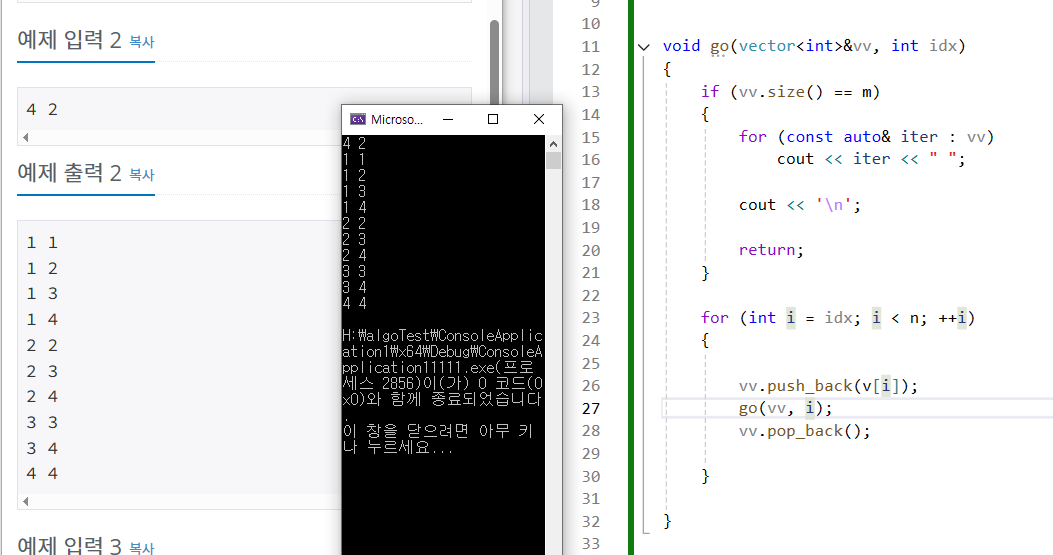
1번. 개수가 작으면 for문으로 가자.

• 5개 중에서 3개를 뽑아라.
  

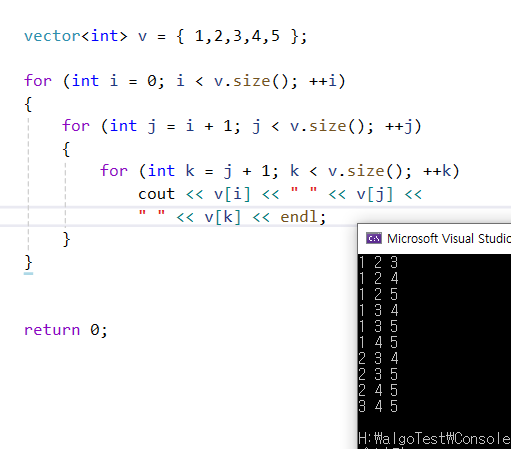
뽑는 개수가 작으면 그냥 for문으로 바로 가자.
이때의 시작 복잡도는 위의 경우 v.size()의 3제곱이다.

2번. 재귀로.

• 잘 생각하면 된다. 5개 중에서 순서 상관없이 중복처리된 3개 어떻게 뽑을까?? 를 생각하면 된다.

• 아이디어.
  -> dfs 인덱스 값이 중요하다. idx + 1 이 아니다!!
  

• 코드
  : 인덱스값을 증가시켜서 앞의 인덱스로 오지 않게 해야 한다.
  

관련 문제

백준 15650 : N과 M (2)

순열_260414

원리
: 순서를 고려하는 것이므로, 다시 앞의 value를 참조하는 것이므로, go 함수에서 idx값 필요 없다.

• 순열은 순서 를 고려해서 배치하는 것이므로, 이미 방문된 원소도 다시 방문할 수 있게 해야 한다.

• 그런데 이 때 중복을 처리하는 것이므로, bool 변수 필요하다.

관련 문제

• 백준 : 135649 N과 M (1)

---

아래는 이전 작성.

언제 순열? 언제 조합? 251005

• 1) 조합의 경우
  : 5명 사람 중에서 3개를 뽑아야할때

• 2) 순열의 겨우
  : 5명 사람 중에서 3명을 뽑는데 , 순서에 상관 있는 조건이 붙은 경우,

// 예를 들면, 들어온 순서대로 번호표를 받는다.
-> 순열이다.

next_permutation으로 부분순열 : 260414

: 5개 중에서 3개를 뽑으라고 하는 경우, next_permutation 사용하면 안된다.

-> reverse를 사용하면 된다.

https://velog.io/@kwt0124/260411%EA%B3%B5%EB%B6%80-%ED%95%98%EC%9E%90

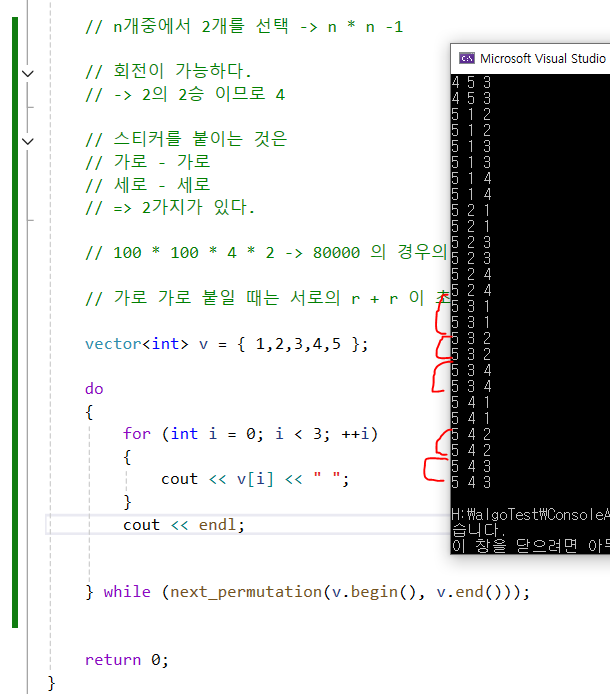
부분 순열에 대해서_251005

---

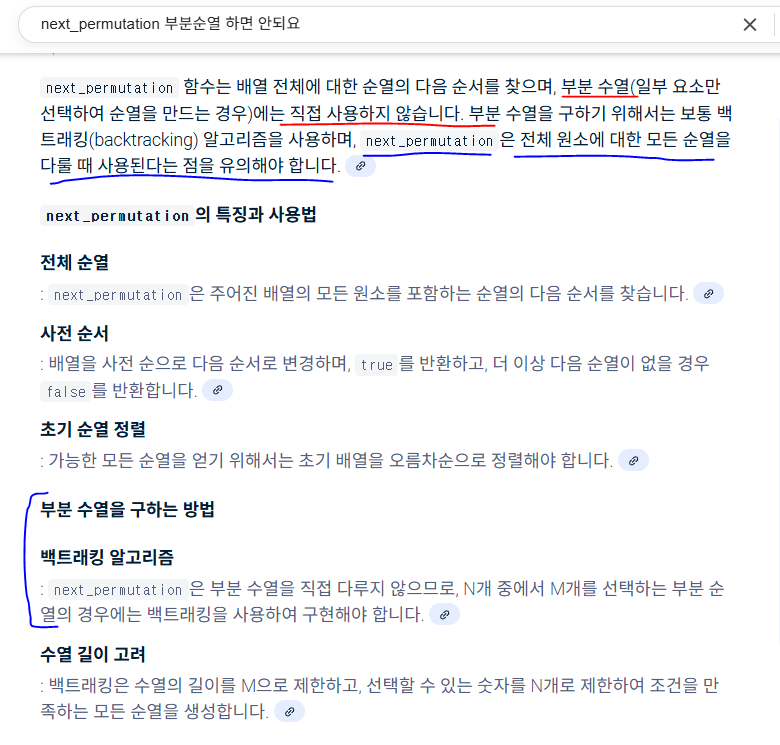
경우의 수 4가지를 알아보자.

• 반드시 숙지해야 함.

순열

• 순열이란 순서에 상관 있게 선택하는 경우이다.

• 1 2 3 4에서 3개를 뽑는다고 해보자.
  -> 아래의 숫자들을 보면, 순서가 모두 다르게 배치된 것을 확인할 수 있지만 , 조합은 그렇지 않다.// 아래에 있다.

123 / 124 / 132 / 134 / 142 / 143
213 / 214 / 231 / 234 / 241 / 243
312 / 314 / 321 / 324 / 341 / 342
412 / 413 / 421 / 423 / 431 / 432

• 이 때의 수식은 4! / (4 - 3)! 이다.

-> 총 24개다.

관련 문제 : n 과 m 1번

• 문제
  

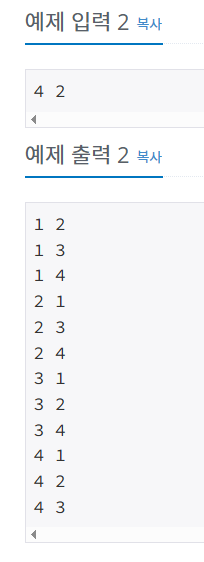
• 코드
  

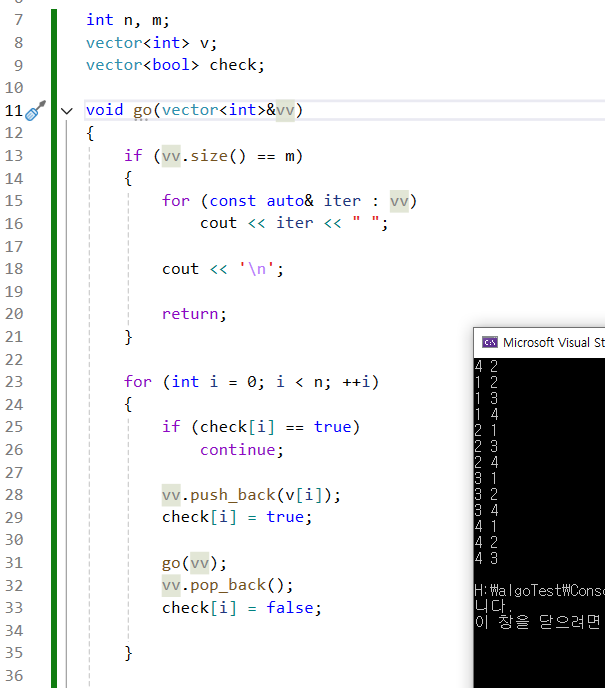
조합

• 조합이란 순서에 무관하게 동일한 경우, 를 나타내는 겨우이다.

• 1 2 3 4 에서 3개 뽑는 조합은

123 / 124 / 134
234 / 이고
-> 순서에 상관 없이 그냥 어떤 숫자를 이미 뽑았다고 하면 만들 필요 없다는 것이다.

• 순열의 경우 321도 되지만, 조합은 순서 무관하게 뽑기만 하는 경우이다.

• 4c3 이고 이 때의 수식은
  4! / 3! 이다.

-> 총 4개다.

관련 문제 : n과 m 2번

• 문제
  

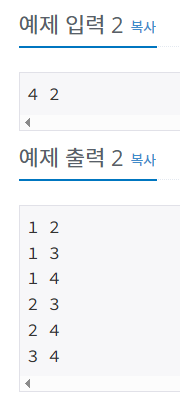
• 코드
  

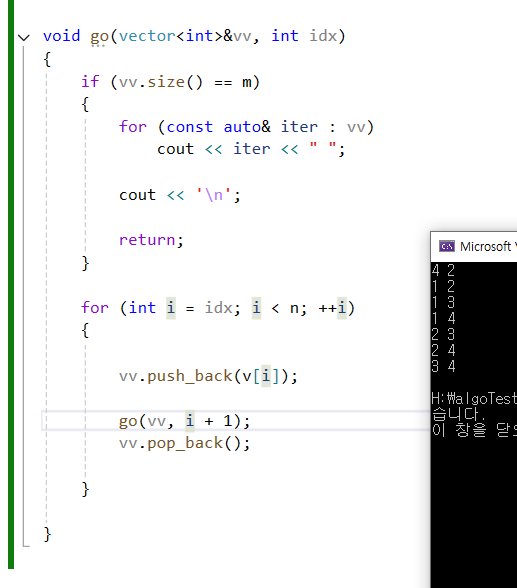
중복 순열

• 중복 순열이란 순서에 상관있게 중복되는 거를 뽑는거다.

• 1 2 3 4 중에서 3개를 뽑아보자.

111 112 113 114 123 124 134

• 이런식으로 매순간 4번을 선택하므로

-> 4 4 4의 시간복잡도를 가진다.

관련 문제 : n과 m 3번 문제

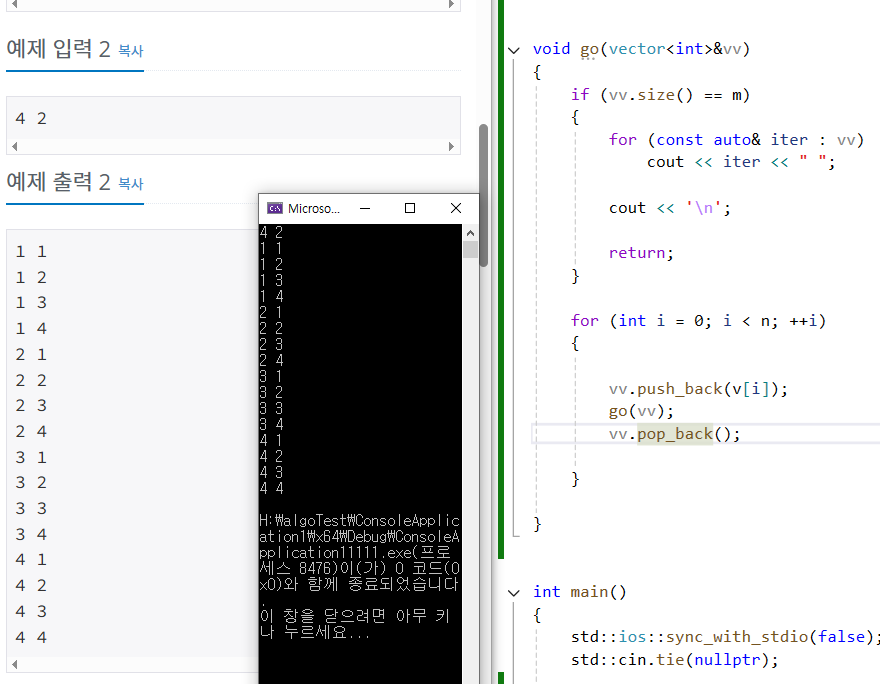
for문으로 만든 중복 순열_251025

• 16985 Maaaaaaaze 에사 사용함.
  

중복 조합

• 중복 조합이란, 중복을 하면서 순서에 관계 없이 동일한 거를 제외하는 거다.

관련문제 : n과 m 4번 문제