누적합이란?

: 인덱스마다의 이전원소값과 현재 원소값을 누적시키면서
메모이제이션 형태로 저장함.
연속된 원소의 값을 구해야 할때 사용하는 알고리즘 기법.

메모이제이션 인덱스가 의미하는 바는
0번째 인덱스 부터 n번째 인덱스 까지의 합

왜 누적합을 해야하는 것일까? 240107 눈 오는 일요일_율동공원 사람 많어...

: 핵심이고, 생각해보기

• 참고 : 백준 구간합 구하기 11659번 문제
  : 시간 제한은 1초, 즉 1억번 연산가능하고, 아래 문제를 읽어보면,
  정리하자만, 보통 풀이로 진행하면, N M번 만큼의 시간복잡도를 가짐.
  -> 10만 10만 -> 10 10 100000000 ,, 1억 넘어감.
  
• 이 때 누적합을 사용하면, 데이터를 입력할 때 이미 psum을 넣어놓은 상태에서 진행하면,
  인덱스 접근으로 최대 복잡도 psum[n] - p[1] 이라고 하면, 1의 복잡도를 가지고 오고, m번 횟수만큼 진행하면 o(m) 의 시작복잡도를 가지고 옴.

어떻게 사용될까?

5번에서 8번까지의 연속된 값이 필요하다고 한다면?
d[8]번 : 즉 0번 인덱스부터 8번 인덱스 까지의 합임.
d[5]번 : 즉 0번 인덱스부터 5번 인덱스 까지의 합임.

이해하기

d[8] - d[5] 라고 한다면 ?
-> 6번에서 7,8번가지의 원소의 합이 남게됨.
추가적으로 여기서 v[5] 원소를 더하면됨.

구현해보면?

d[n] = d[n - 1] ~ 으로 시작해야 하는데,
반복적인 코드 구현을 위해

• 시작 인덱스 n은 1부터 시작해야 겠다.
  0부터 시작하면 언더플로우 발생함.

// 누적합 메모이제이션을 만들기 위해
// 원소의 초기값 인덱스를 1로 시작해서 n으로 끝마치게 해야함.
for(int i = 1; i <= n; ++i)
{
cin >> v[i];
d[i] = d[i - 1] + v[i];

}
=> 이렇게 나타낼 수 있음.
이렇게 하면 , 위의 이해하기를 좀 다른 방식으로 코드 접근해야 함.

• 의미하는 바
  d[1] : v[0]
  d[2] : v[0] + v[1]
  d[3] : v[0] + d[1] + d[2]
  이렇게 되므로

만약에 4번 인덱스 부터, 8번 인덱스까지의 연속 합을 구하라고 한다면?

int sum = d[8 + 1] - d[4]

: 이런식으로 풀면됨.

관련문제

: 백준 2559번 수열

출처

: 2022 카카오 6번 문제
-> 효율성 틀렸다...

• 이차원 배열의 인덱스 ~ 인덱스 하기에는 조건 때문에 시간복잡도가 어마어마해서 효율성에서 빵점 맞았다.

그림

: 0보다 큰 컨테이너의 갯수를 구하라! 가 6번 문제의 답이다.

관련 문제

https://www.acmicpc.net/problem/15724

https://www.acmicpc.net/problem/19951

문제

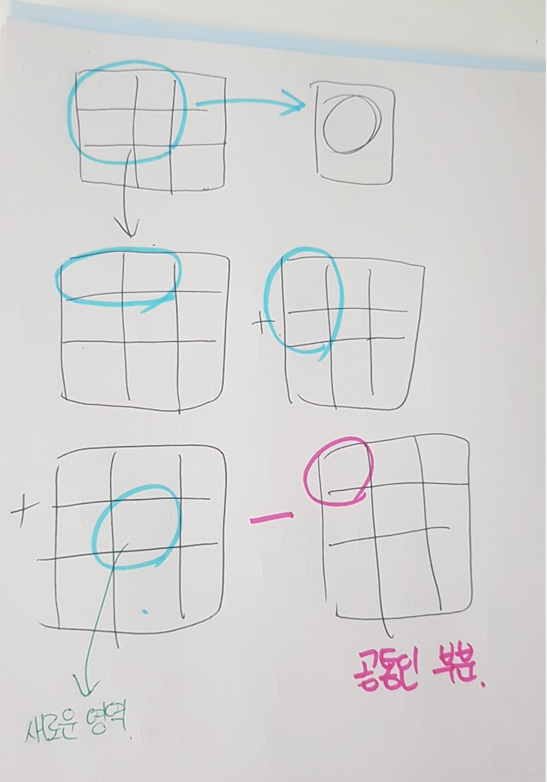
: 백준 2167번 2차원 배열의 합

점화식 구현하기!

• 앞서서 가로와 세로값은 따로 구해줘야 한다.

//참고한 블로그 님
https://sorious77.tistory.com/125