- 인프런의 김태원 강사님의 강의를 공부하고 정리한 내용입니다.
- 이것이 코딩테스트다를 공부하고 정리한 내용입니다.
타당한지 증명하기 250521
: 그리디 이다.
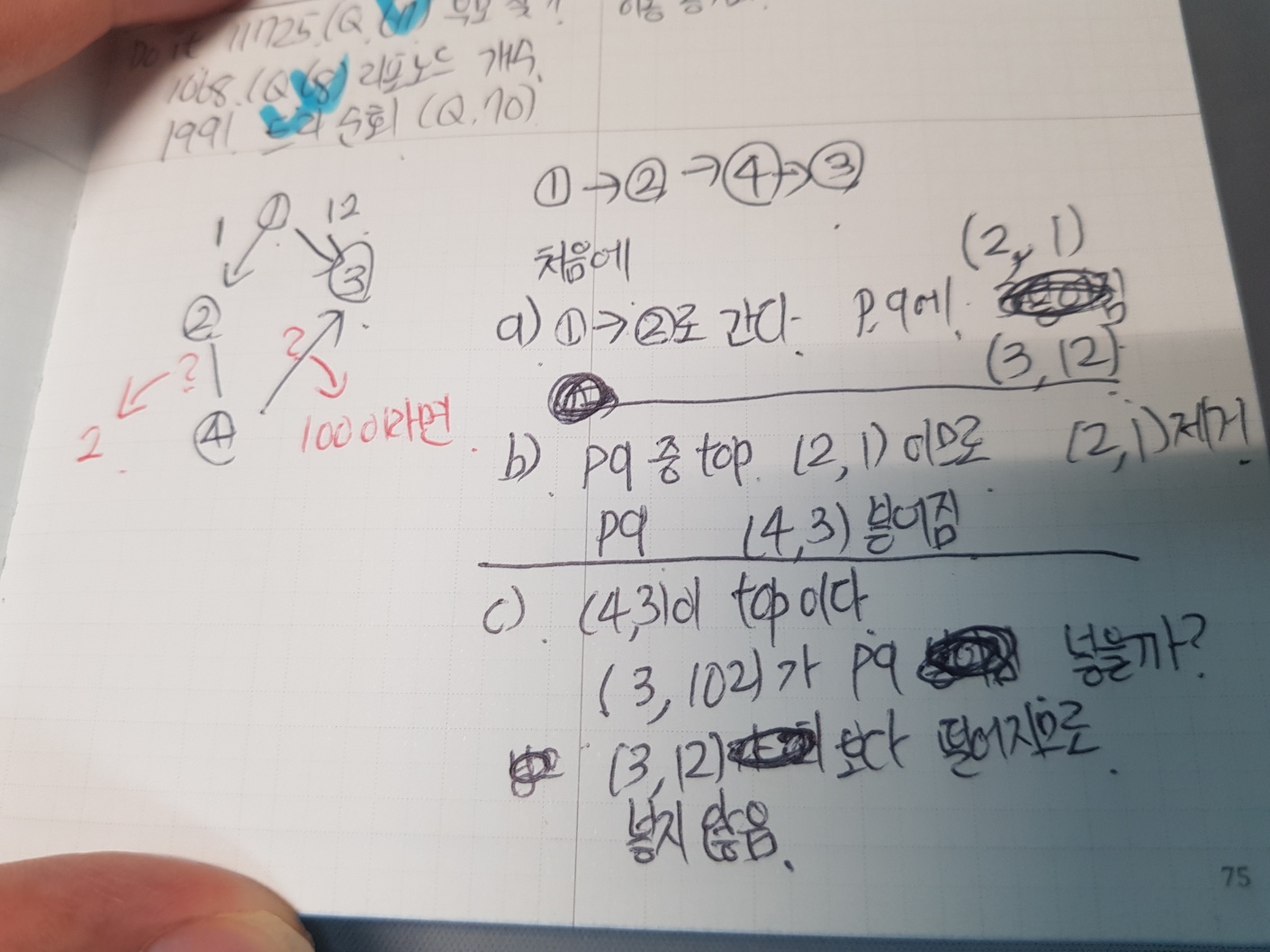
예시 1번.
- 아래의 그림에서 1->3번으로 가는것이 아니라, 1->2 번 정점을 거쳐서 가는 것이 최고일 수도 있지 않냐? 에 대한 그림이다.

- 2번에서4번으로 가는 간선과 4번에서 3번으로 가는 간선이
음의 간선이 아닌 이상 이미 1에서 3으로 가는 방법이 최선이다.
성립하는 이유
: 매순간 최선의 선택을 하는 그리디이다.
- 그리고 다익스트라는 시작정점에서 타겟정점으로 가는 최소비용을 구하는 것일 텐데 반드시 1번 정점에서 시작해야 하는 조건이 걸려있기 때문이다.
- 다익스트라는 음의 간선이 없다.
예시 2번.
- 1번에서 3번으로 가는 방법이 처음에는 최선의 방법으로 선택되지 않지만, 다익스트라는 pq이기 때문에 추후에 라도 최소비용이 결정된다.
-
그리고 백준 1916번 문제는 visited를 사용해야 문제가 맞는데,
visited = true는 bfs와는 다르게 dist 조건문이 아닌
pq에서 pop한 다음에 visited = true 처리해야 한다.
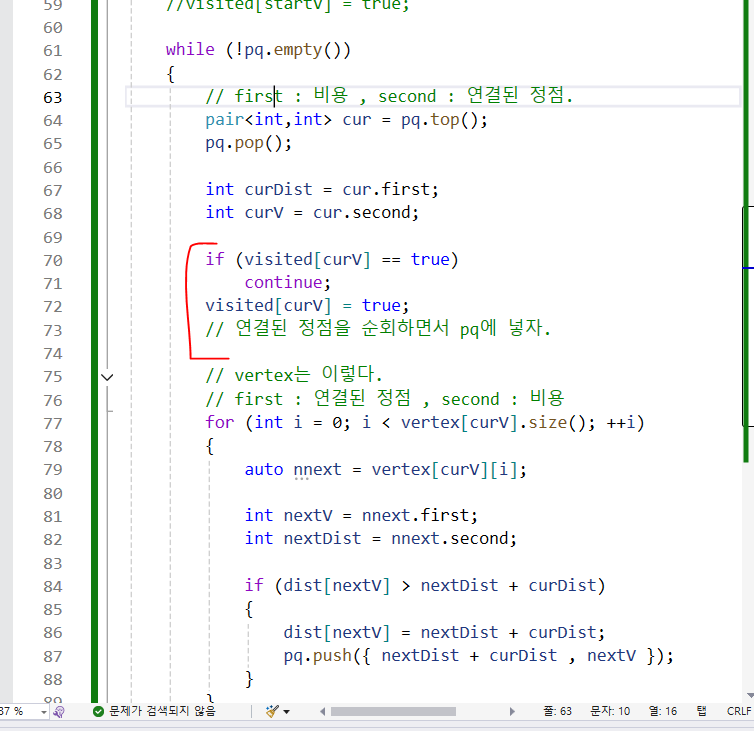
- 이유 dist 조건문에서 한다는 것은 새로운 정점을 pq에 넣는 것인데 여기다가 visited 처리하는 것은 새로운 정점에 대한 처리이다. 그러므로 이미 pq완료된 정점인 순간인 70번 줄에서 73번 줄에서 visited 체크해야 한다.
예시 코드
Do it! 56번, 57번, 58번 코드 참고.
but, visited는 필요 없다.
우선순위 큐
https://velog.io/@kwt0124/%EC%9A%B0%EC%84%A0%EC%88%9C%EC%9C%84%ED%81%90
가장 낮은 dist를 얻어야 하므로
priority_queue<pair<int,int> , vector<pair<int,int>> ,greater<pair<int,int>> pq;
를 사용하자.
bfs 와는 다른 점
인접한 모든 정점을 넣는 것이 아니라 타겟 정점으로부터 dist 테이블에 기록된 최소비용의 정점을 넣음.
240105 추가.
bfs 는 모든 정점에 대한 가중치 없음
다익스트라의 경우, 가중치가 존재함.
어떻게 접근할 것인가?
- distTable을 최대값 1e9 로 설정하기
- 시작 정점의 방문 기록하기
- 시작 정점에 인접한 정점들의 dist 테이블 갱신
- distTable 에서 가장 작은 값이 타겟 노드다.
- 타겟 노드로 3번을 진행
- 모든 노드 처리 후 dist테이블도 완료됨.
-> 이 때의 시간 복잡도 최악 V 제곱임.
- 이유 : 최단 거리 탐색 : V / 해당 정점으로부터 인접한 정점 검사 : v
- 각 정점마다 시작점까지의 최단 경로를 가지고 있는 cost 값이 필요함.
- 우선순위 큐를 이용해서 매순간 최소비용을 찾는 시간 복잡도 V를 제거하자!
우선순위 큐 비교할 때
-
- struct::cmp 사용시

- 외부에서 사용시 이렇게 선언해야 함

- struct::cmp 사용시
-
- 구조체내의 operator 비교 연산자 사용시, 반드시 < , >
2개의 연산자 만들어야 함.
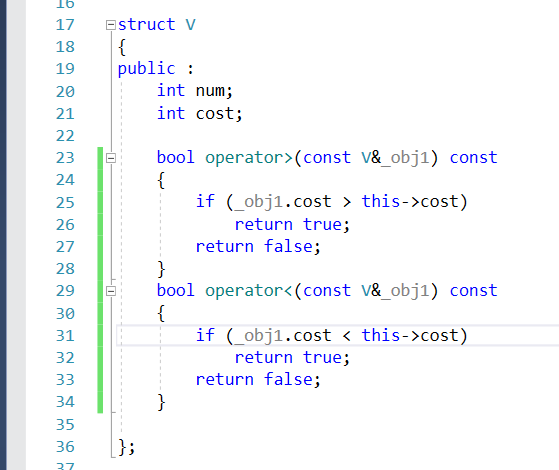
- 외부 사용시 그냥 사용하면 됨.

- 구조체내의 operator 비교 연산자 사용시, 반드시 < , >
결과
- -> 여기까지가 내 생각 정리한 부분. 아래는 책에 있는 내용임.
다익스트라 알고리즘이란?
: 매순간 최소의 비용을 나타내는 정점을 선택해서 distTable을 갱신해서
최단 거리를 구하는 알고리즘이다.
개념
- 한 노드에서 모든 노드까지 이동하는데 최단 경로를 구함.
- 아직 방문하지 않는 노드중에서 가장 비용이 작은 노드를 선택해나가는 과정.
알고리즘 분류
- 그리디 + bfs + 그래프 + distTable
어떻게 만들것인가
- 1) 타겟노드를 기준으로 해서 모든 노드번호까지의 최단 경로를 지정하는
dp를 만들어야 함. - 2) 연결된 모든 노드들과의 거리를 계산해서 dp[노드 번호]와 비교를 함.
- 3) dp보다 계산 결과가 작을 경우에 dp를 갱신함.
- 4) 이 때 거쳐서 지나간다라는 것을 염두해서 갱신해야 함.
- 5) 시작 노드 완료후, 연결된 정점 중에서 비용이 가장 작은 노드를
선택해서 연결된 노드에 관해 반복 진행함.
dp[node]의 의미
: 타겟 노드에서 node번호까지 이동하는데 최단경로를 의미함.
중요한 부분
: 다음 cost 비용을 계산하는 것은 현재 자기 자신까지의 cost와
외부에서 입력된 cost를 더한 후 dist값과 비교하는 것이다.
이 부분이 제일 중요하다.
- 그림을 보면 확실히 인지할 수 있다.
1에서 4를 거쳐서 3을 가는 cost가 1에서 3으로 가는 cost 보다 작기 때문에./
핵심!
0) 각 정점에 대한 distTable을 만들자.
- distTable을 통해서 가장 작은 dist를 추려낼 것이다!
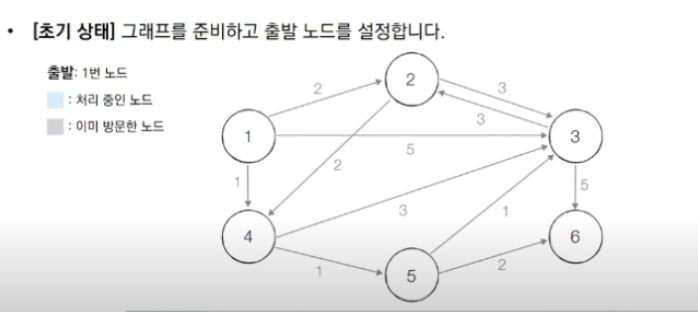
1) 시작 정점을 1이라고 가정하자. 1번 정점의 dist는 0이 되고, 나머지 정점들을 모두 무한대 값으로 설정한다.
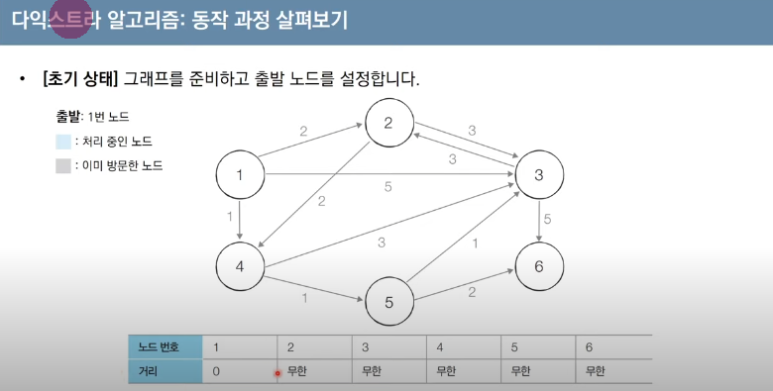
1-1) 시작정점으로 부터 연결된 정점들까지의 거리를 저장공간에 집어넣는다.
2) 정점 중 체크 안된 정점 중에서 값이 가장 작은 놈을 체크 후,
해당 정점으로부터 이동 가능한 모든 정점의 값을 갱신하는데,
갱신할때는 타겟으로 잡은 곳의 값에 연결된 비용을 더한 값과
연결된 정점들의 현재 저장된 값을 비교한다.
현재의 값과, 갱신된 값을 비교해 갱신여부를 확인한다.
현재의 값과 갱신된 값중 가장 작은 값을 적용한다.

3) 2번 작업을 반복한다.
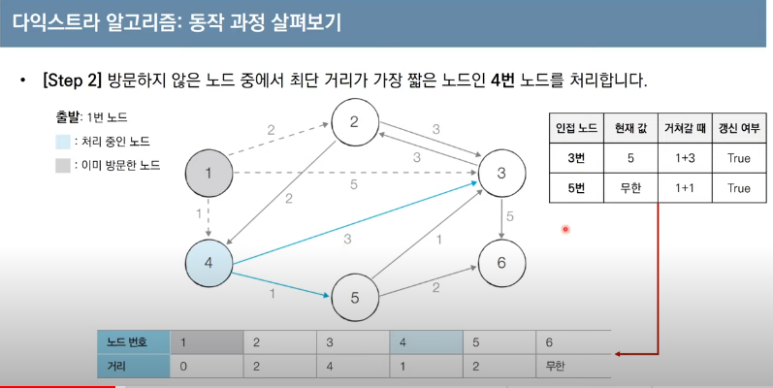
- 현재 4번 정점을 이용해 갱신하고 있는 과정이다.
기존 dp[3] (1번 정점에서 3번 정점의 dist)은 5였지만, 1번 -> 4번 -> 3번으로 갈때가 4 값이고, 5보다도 더 작으므로, 갱신함.
=> 이런식으로 반복하다보면, 모든 정점까지 체크 완료된 테이블이 만들어진다.
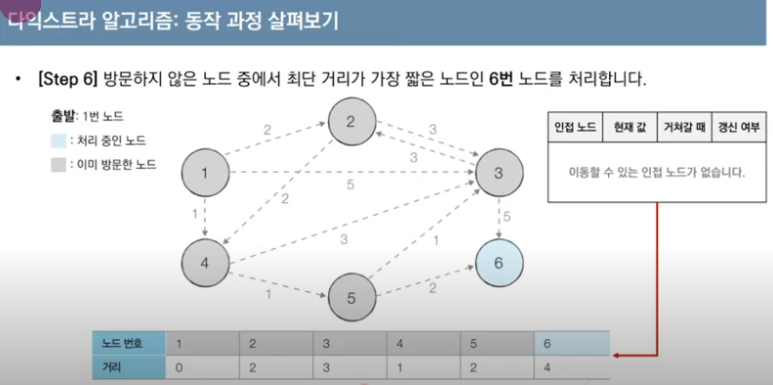
2번 작업에서의 의구심을 증명하기
-> 의구심이 생길 수 있는 부분이, 체크된 정점을 다시 확인이 불가능한 시퀀스인데, 만약에 다른 정점을 통해 4번 노드의 값이 최단거리로 갱신될수 있지 않을까 생각을 할 수 있다.
아래의 증명 과정을 통해 다익스트라는 그리디 알고리즘이라는 것을 생각할 수 있다. 매순간 최소의 비용은 나타내는 정점을 선택해서 distTable을 갱신해서
최단 거리를 구하는 알고리즘이다.
구종만 p.927 참고. 정당성의 증명이 있다. (250521)
하지만 이것을 증명할 수 있는 조건이 있다.
1번 정점이 완료 된 후에 2,3,4,5,6번 정점 중 가장 작은 거리에 있는 정점을 선택한다
이 용어가 의미하는 것은 그 이외의 값으로 4번 정점으로 들어올때는 더 낮은 비용을 만들 수 없다는 것을 의미한다. 왜냐하면 거리는 모두 양수이기 때문이다.
거리가 음수이면 이 증명은 잘못된 것이다.
- 아래 내용은 이상함.

확인을 해보자.
- 2번 정점은 거리가 2
- 3번 정점은 거리가 4
- 4번 정점은 거리가 1
- 5번 정점은 거리가 2
- 6번 정점은 거리가 무한대
-> 4번이 선택된다. 2번이 4번으로 들어 올수 있지만, 2번의 현재값은 2이다.
갱신이 되더라고 4번의 값 1보다는 작을 수 없다.
-> 다른 정점이 연결되어있다고 가정한다면, 5번이 연결되어 있다고 가정해보자.
전제 조건으로 체크안된 정점 중 가장 작은 정점이기 때문에 (현재 4번은 1이다.)
5번은 다른 정점에 의해 1초과된 값으로 되어 있을 것이다! 라고 확증이 가능하므로, 4번 값은 더 낮은 값으로 갱신이 될수 없다.

고찰
: 코드를 어떻게 작성할 것인가?
-
- 시작점을 제외한 나머지값을 큰값이나, 무한으로 설정하자.
-
- 위의 정점마다 시작점부터 해당 정점까지 오는데의 비용을 가지고 있으므로
pair를 이용하자.
- 위의 정점마다 시작점부터 해당 정점까지 오는데의 비용을 가지고 있으므로
-
- 시작점 끝나고 다음 정점 시작할때를 생각해보면, 가장 작은 비용인 친구를 선택해서 뽑고, 해당 정점에 연결된 친구들을 확인하는 것이므로
우선순위큐, top()이 낮게 설정되어있는 상태를 해야한다.
그러므로
: 코드를 보면 우선순위 큐 first 넣을때 음수값으로 넣었다.
- 시작점 끝나고 다음 정점 시작할때를 생각해보면, 가장 작은 비용인 친구를 선택해서 뽑고, 해당 정점에 연결된 친구들을 확인하는 것이므로
-
- 타겟으로 정한 친구 선택후에, 다시 지나치지 않기 위해서 불변수가 필요하다.
우선순위 큐 사용하지 않는 코드
#include <iostream>
#include <mutex> // mutex 를 사용하기 위해 필요
#include <thread>
using namespace std;
#pragma comment(lib, "StaticLib1")
#include <vector>
#include <filesystem>
#include <queue>
// 각 정점마다 연결되는 정점들이 있음.
struct V
{
int num;
int cost;
};
vector<vector<V>> v(7);
vector<int> best(7, 1e9);
vector<bool> visited(7, false);
int MostSmall()
{
int vertex = -1;
int cost = 1e9;
// 방문하지 않은 것들 중에서 가장 cost 비용이 작은 정점을 추출하자.
for (int i = 0; i < best.size(); ++i)
{
if (best[i] < cost && visited[i] == false)
{
cost = i;
}
}
return cost;
}
int main()
{
// 1번 노드가 시작점.
// 모든 정점의 최소 비용을 구하자.
{
v[1].push_back({ 2,2 });
v[1].push_back({ 4,1 });
v[1].push_back({ 3,5 });
v[2].push_back({ 4,2 });
v[2].push_back({ 3,3 });
v[3].push_back({ 2,3 });
v[3].push_back({ 6,5 });
v[4].push_back({ 3,3 });
v[4].push_back({ 5,1 });
v[5].push_back({ 3,1 });
v[5].push_back({ 6,2 });
}
// 1. 타겟 정점으로부터 가장 최소 비용을 잡은 후, -> 방문 체크하자.
// 2. 인접한 정점의 dp 테이블 갱신.
int startNum = 1;
best[startNum] = 0;
visited[startNum] = true;
int edge = 1e9;
// 인접한 것들 중에서
// 1번 정점부터 시작함.
// 각 cost 갱신하기
// 시작 할때는 비교 안하고 그냥 셋팅.
for (int i = 0; i < v[startNum].size(); ++i)
{
int vertex = v[startNum][i].num;
best[vertex] = v[startNum][i].cost;
}
// 여기서 반복함.
// 언제 끝낼지를 확인해야 하는데. 내가 아는 정보는 정점들 중에서 startNum 만 끝남.
for (int k = 0; k < v.size() - 1; ++k)
{
// 최소값 구하기
int targetV = MostSmall();
if (targetV == 1e9)
break;
visited[targetV] = true;
for (int i = 0; i < v[targetV].size(); ++i)
{
int vertex = v[targetV][i].num;
int cost = v[targetV][i].cost + best[targetV];
// 방문하지 않은 것들 중에서 비교하자.
if (best[vertex] > cost)
{
best[vertex] = cost;
}
}
}
cout << endl;
// 찾은 정점을 통해서 또 진행..
}
위 코드를 보면,
방문하지 않은 것중에서 최소비용을 얻는 작업을 하고 있음. (MostSmall) ->이 비용을 줄이기 위해
인접한 정점에 cost 작업을 할 때, 그와 동시에 priority_queue 에 삽입하자.
삽입하는 데이터는 최소비용인 cost 와 인접한 정점을 넣으면 될 듯함.
왜냐하면 MostSmall 함수에서 best 중에서 가장 작은 정점을 반환하고 있기 때문임.
우선순위큐 사용 코드
#include <iostream>
#include <mutex> // mutex 를 사용하기 위해 필요
#include <thread>
using namespace std;
#pragma comment(lib, "StaticLib1")
#include <vector>
#include <filesystem>
#include <queue>
// 각 정점마다 연결되는 정점들이 있음.
struct V
{
public :
int num;
int cost;
};
struct cmp
{
bool operator()(const V& _a, const V& _b)
{
return _a.cost > _b.cost;
}
};
// 이상하게 class 외부에다가 해줘야 오류 해결됨..
//bool operator>(const V& _a, const V& _b)
//{
// return _a.cost > _b.cost;
//}
//
//bool operator<(const V& _a, const V& _b)
//{
// return _a.cost < _b.cost;
//}
vector<vector<V>> v(7);
vector<int> best(7, 1e9);
vector<bool> visited(7, false);
int MostSmall()
{
int vertex = -1;
int cost = 1e9;
// 방문하지 않은 것들 중에서 가장 cost 비용이 작은 정점을 추출하자.
for (int i = 0; i < best.size(); ++i)
{
if (best[i] < cost && visited[i] == false)
{
cost = i;
}
}
return cost;
}
int main()
{
// 1번 노드가 시작점.
// 모든 정점의 최소 비용을 구하자.
{
v[1].push_back({ 2,2 });
v[1].push_back({ 4,1 });
v[1].push_back({ 3,5 });
v[2].push_back({ 4,2 });
v[2].push_back({ 3,3 });
v[3].push_back({ 2,3 });
v[3].push_back({ 6,5 });
v[4].push_back({ 3,3 });
v[4].push_back({ 5,1 });
v[5].push_back({ 3,1 });
v[5].push_back({ 6,2 });
}
// 1. 타겟 정점으로부터 가장 최소 비용을 잡은 후, -> 방문 체크하자.
// 2. 인접한 정점의 dp 테이블 갱신.
int startNum = 1;
best[startNum] = 0;
int edge = 1e9;
// 인접한 것들 중에서
priority_queue<V , vector<V> , cmp> pq;
// 시작점을 넣자.
pq.push({ 1,0 });
while ( !pq.empty())
{
V targetV = pq.top();
pq.pop();
int targetNum = targetV.num;
int targetNumCost = targetV.cost;
//if (visited[targetNum] == false)
// continue;
//visited[targetNum] = true;
// 인접한 정점들을 pq에 넣고, // 그리고 dp 값 갱신.
for (int i = 0; i < v[targetNum].size(); ++i)
{
int vertex = v[targetNum][i].num;
int cmpData = v[targetNum][i].cost + best[targetNum];
if (best[vertex] > cmpData)
{
best[vertex] = cmpData;
pq.push(v[targetNum][i]);
}
}
}
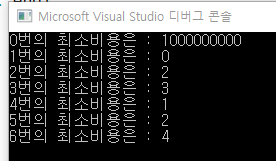
for (int i = 0; i < best.size(); ++i)
{
cout << i << "번의 최소비용은 : " << best[i] << endl;
}
cout << endl;
// 찾은 정점을 통해서 또 진행..
}
-> 위의 코드는 pq에 대해서 공부가 덜 된 상태에서 작성한 코드다. 240518
- 이런식으로 변경하면 된다.
priority_queue 를 greater 로 설정함.
다익스트라의 경우, 최소힙 즉 top이 가장 낮은 값으로 우선순위를 만들어야한다.
그래서 greater를 작성해야 한다.
#include <iostream>
#include <mutex> // mutex 를 사용하기 위해 필요
#include <thread>
using namespace std;
#include <vector>
#include <filesystem>
#include <queue>
// 각 정점마다 연결되는 정점들이 있음.
struct V
{
public:
int num;
int cost;
bool operator>(const V& _obj) const
{
return cost > _obj.cost;
}
};
struct cmp
{
bool operator()(const V& _a, const V& _b)
{
return _a.cost > _b.cost;
}
};
vector<vector<V>> v(7);
vector<int> best(7, 1e9);
vector<bool> visited(7, false);
int MostSmall()
{
int vertex = -1;
int cost = 1e9;
// 방문하지 않은 것들 중에서 가장 cost 비용이 작은 정점을 추출하자.
for (int i = 0; i < best.size(); ++i)
{
if (best[i] < cost && visited[i] == false)
{
cost = i;
}
}
return cost;
}
int main()
{
// 1번 노드가 시작점.
// 모든 정점의 최소 비용을 구하자.
{
v[1].push_back({ 2,2 });
v[1].push_back({ 4,1 });
v[1].push_back({ 3,5 });
v[2].push_back({ 4,2 });
v[2].push_back({ 3,3 });
v[3].push_back({ 2,3 });
v[3].push_back({ 6,5 });
v[4].push_back({ 3,3 });
v[4].push_back({ 5,1 });
v[5].push_back({ 3,1 });
v[5].push_back({ 6,2 });
}
// 1. 타겟 정점으로부터 가장 최소 비용을 잡은 후, -> 방문 체크하자.
// 2. 인접한 정점의 dp 테이블 갱신.
int startNum = 1;
best[startNum] = 0;
int edge = 1e9;
// 인접한 것들 중에서
priority_queue<V, vector<V>, greater<V>> pq;
// 시작점을 넣자.
pq.push({ 1,0 });
while (!pq.empty())
{
V targetV = pq.top();
pq.pop();
int targetNum = targetV.num;
int targetNumCost = targetV.cost;
//if (visited[targetNum] == false)
// continue;
//visited[targetNum] = true;
// 인접한 정점들을 pq에 넣고, // 그리고 dp 값 갱신.
for (int i = 0; i < v[targetNum].size(); ++i)
{
int vertex = v[targetNum][i].num;
int cmpData = v[targetNum][i].cost + best[targetNum];
if (best[vertex] > cmpData)
{
best[vertex] = cmpData;
pq.push(v[targetNum][i]);
}
}
}
for (int i = 0; i < best.size(); ++i)
{
cout << i << "번의 최소비용은 : " << best[i] << endl;
}
cout << endl;
// 찾은 정점을 통해서 또 진행..
}- 결과
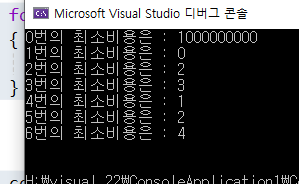
더 생각해야 할 부분.
- 인접한 정점 중에서 최소비용을 선택하고, 해당 정점을 pop 한 후, 방문처리를 해야할까에 대해서?
: 맨 처음의 distTable 셋팅시 무한으로 했음.
-> 이를 이용하면 됨. - dp 적인 관점에서 보면, 최소비용을 선택할 경우, 다른 경로들이 최소비용보다 크다는 것을 의미함.
-> 이것은 어떻게 해서 지금의 최소비용 정점으로 돌아온다고 하더라도, 당연하게도!! 최소 비용 정점보다 작을 수는 없음.
(상식적인 부분임)
https://github.com/ndb796/python-for-coding-test/blob/master/9/2.cpp
- 나는 위의 우선순위 큐 코드에서 조건 처리를 못했는데,
위의 참고자료를 보면, distTable 을 통해서 조건 처리하고 있는 것을 확인할 수 있음.
문제
: 페이지 230과 같은 그림이 주어지고, 페이지 249와 같은 입력이 주어졌을때 각 정점에 도착하는데 최단 거리는 어떻게 될것인가?
-
그림
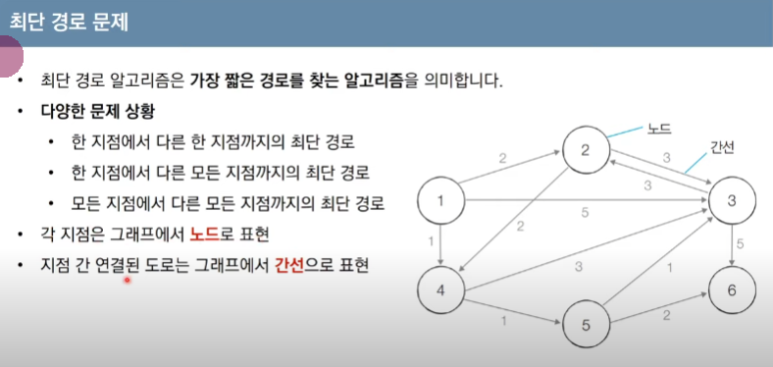
-
예제는 책에 있는 거 참고 : 페이지 249
소스코드 - 이코테 책에 있는 코드
- 내림차순으로 설정해야 함.
#include <iostream>
#include <vector>
#include <queue>
#define INF 1e9 // 무한을 의미하는 값으로 10억을 설정
using namespace std;
// 노드의 개수(N), 간선의 개수(M), 시작 노드 번호(Start)
// 노드의 개수는 최대 100,000개라고 가정
int n, m, start;
// 각 노드에 연결되어 있는 노드에 대한 정보를 담는 배열
vector<pair<int, int> > graph[100001];
// 최단 거리 테이블 만들기
int d[100001];
void dijkstra(int start) {
priority_queue<pair<int, int>, vector<pair<int,int>>,
less<pair<int,int>>> pq;
// 시작 노드로 가기 위한 최단 경로는 0으로 설정하여, 큐에 삽입
pq.push({ 0, start });
d[start] = 0;
while (!pq.empty()) { // 큐가 비어있지 않다면
// 가장 최단 거리가 짧은 노드에 대한 정보 꺼내기
int dist = pq.top().first; // 현재 노드까지의 비용
int now = pq.top().second; // 현재 노드
pq.pop();
// 현재 노드가 이미 처리된 적이 있는 노드라면 무시
//210806 이부분 이해하는 것이 중요함.
//정점의 테이블 값보다 값이 크다면 밑의 반복문을 할 필요가 없다.
if (d[now] < dist) continue;
// 현재 노드와 연결된 다른 인접한 노드들을 확인
for (int i = 0; i < graph[now].size(); i++) {
int cost = dist + graph[now][i].second;
// 현재 노드를 거쳐서, 다른 노드로 이동하는 거리가 더 짧은 경우
if (cost < d[graph[now][i].first]) {
d[graph[now][i].first] = cost;
pq.push(make_pair(cost, graph[now][i].first));
}
}
}
}
int main(void) {
cin >> n >> m;
// 모든 간선 정보를 입력받기
for (int i = 0; i < m; i++) {
int a, b, c;
cin >> a >> b >> c;
// a번 노드에서 b번 노드로 가는 비용이 c라는 의미
graph[a].push_back({ b, c });
}
// 최단 거리 테이블을 모두 무한으로 초기화
fill(d, d + 100001, INF);
// 다익스트라 알고리즘을 수행
dijkstra(1);
// 모든 노드로 가기 위한 최단 거리를 출력
for (int i = 1; i <= n; i++) {
// 도달할 수 없는 경우, 무한(INFINITY)이라고 출력
if (d[i] == INF) {
cout << "INFINITY" << '\n';
}
// 도달할 수 있는 경우 거리를 출력
else {
cout << d[i] << '\n';
}
}
}소스코드 - compare 함수를 이용한 코드
#include <iostream>
#include <vector>
#include <queue>
#define INF 1e9 // 무한을 의미하는 값으로 10억을 설정
using namespace std;
// 노드의 개수(N), 간선의 개수(M), 시작 노드 번호(Start)
// 노드의 개수는 최대 100,000개라고 가정
int n, m, start;
// 각 노드에 연결되어 있는 노드에 대한 정보를 담는 배열
vector<pair<int, int> > graph[100001];
// 최단 거리 테이블 만들기
int d[100001];
//거리가 가장 작은 놈이 top으로 와야 한다..
struct comp
{
bool operator()(pair<int, int>a, pair<int, int>b)
{
return a.first > b.first;
}
};
void dijkstra(int start) {
priority_queue<pair<int, int>, vector<pair<int,int>>, comp > pq;
// 시작 노드로 가기 위한 최단 경로는 0으로 설정하여, 큐에 삽입
pq.push({ 0, start });
d[start] = 0;
while (!pq.empty()) { // 큐가 비어있지 않다면
// 가장 최단 거리가 짧은 노드에 대한 정보 꺼내기
int dist = pq.top().first; // 현재 노드까지의 비용
int now = pq.top().second; // 현재 노드
pq.pop();
// 현재 노드가 이미 처리된 적이 있는 노드라면 무시
//210806 이부분 이해하는 것이 중요함.
//정점의 테이블 값보다 값이 크다면 밑의 반복문을 할 필요가 없다.
if (d[now] < dist) continue;
// 현재 노드와 연결된 다른 인접한 노드들을 확인
for (int i = 0; i < graph[now].size(); i++) {
int cost = dist + graph[now][i].second;
// 현재 노드를 거쳐서, 다른 노드로 이동하는 거리가 더 짧은 경우
if (cost < d[graph[now][i].first]) {
d[graph[now][i].first] = cost;
pq.push(make_pair(cost, graph[now][i].first));
}
}
}
}
int main(void) {
cin >> n >> m;
// 모든 간선 정보를 입력받기
for (int i = 0; i < m; i++) {
int a, b, c;
cin >> a >> b >> c;
// a번 노드에서 b번 노드로 가는 비용이 c라는 의미
graph[a].push_back({ b, c });
}
// 최단 거리 테이블을 모두 무한으로 초기화
fill(d, d + 100001, INF);
// 다익스트라 알고리즘을 수행
dijkstra(1);
// 모든 노드로 가기 위한 최단 거리를 출력
for (int i = 1; i <= n; i++) {
// 도달할 수 없는 경우, 무한(INFINITY)이라고 출력
if (d[i] == INF) {
cout << "INFINITY" << '\n';
}
// 도달할 수 있는 경우 거리를 출력
else {
cout << d[i] << '\n';
}
}
}위 그림과 같이 주어졌을때 1번 노드에서 각 정점으로 향하는 최소 비용을 출력하라
다른 입력
6 11
1 2 2
1 3 5
1 4 1
2 3 3
2 4 2
3 2 3
3 6 5
4 3 3
4 5 1
5 3 1
5 6 2
다른 출력
0
2
3
1
2
4
입력
6 9
1 2 12
1 3 4
2 1 2
2 3 5
2 5 5
3 4 5
4 2 2
4 5 5
6 4 5
출력
2 : 11
3 : 4
4 : 9
5 : 14