📚 이진 탐색 트리 (Binary Search Tree)란 ?

---

이진 트리 기반의 탐색을 위한 자료구조이다.

이진 탐색 트리는 기존 이진트리보다 탐색이 빠르다.

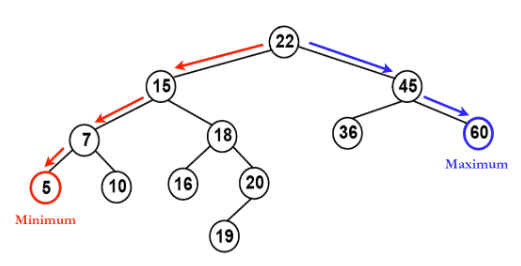
이진 탐색 트리 특징

1. 모든 원소의 키는 유일한 키를 가진다.

   중복값을 허락하지 않는다.

2. 왼쪽 서브 트리 키들은 루트 키보다 작다.
3. 오른쪽 서브 트리의 키들은 루트의 키보다 크다.
4. 왼쪽,오른쪽 서브트리 모두 이진 탐색 트리이다.

📚 탐색, 삽입, 삭제

---

1.이진 탐색 트리 탐색 과정

1. 루트 노드의 키와 찾고자 하는 값을 비교한다. 찾고자 하는 값이라면 탐색을 종료한다.
2. 찾고자 하는 값이 루트 노드의 키보다 작다면 왼쪽 서브 트리로 탐색을 진행한다.
3. 찾고자 하는 값이 루트노드의 키보다 크다면 오른쪽 서브트리로 탐색을 진행한다. 
   위 과정을 찾고자 하는 값을 찾을 때까지 반복해서 진행한다. 만약 그값을 찾지 못하면 그대로 종료한다.

2.이진 탐색 트리 삽입 과정

1. 삽입할 값을 루트 노드와 비교해서 같다면 오류발생 (중복 값 허용 X)
2. 삽입할 값이 루트 노드의 키보다 작다면 왼쪽 서브 트리를 탐색해서 비어있다면 추가하고, 비어있지 않다면 다시 값을 비교한다.
3. 삽입할 값이 루트 노드의 키보다 크다면 오른쪽 서브트리를 탐색해서 비어있다면 추가하고, 비어있지 않다면 다시 값을 비교한다.

1. 6의 값을 삽입한다고 가정한다.
   

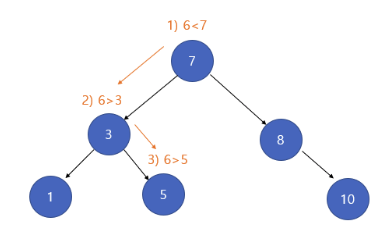
2. 탐색과 비슷하게 삽입하고자 하는 값을 계속해서 비교해가며 삽입할 위치를 찾는다.
   
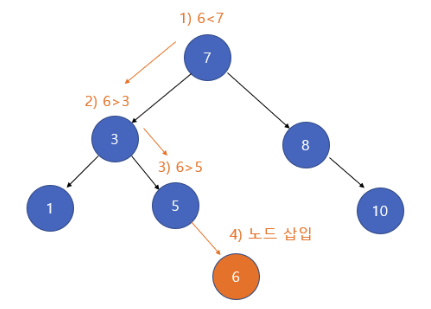
   삽입할 위치가 5의 오른쪽 서브 트리인 것을 찾았으므로, 5의 오른쪽 자식으로 6을 추가하면 된다.

3.이진 탐색 트리 삭제 과정

3가지 경우

1. 삭제하려는 노드가 단말 노드(leaf node) 일 경우
2. 삭제하려는 노드의 서브 트리가 하나인 경우(왼쪽 혹은 오른쪽 서브 트리)
3. 삭제하려는 노드의 서브 트리가 두 개인 경우

1. 삭제하려는 노드가 단말 노드(leaf node) 일 경우

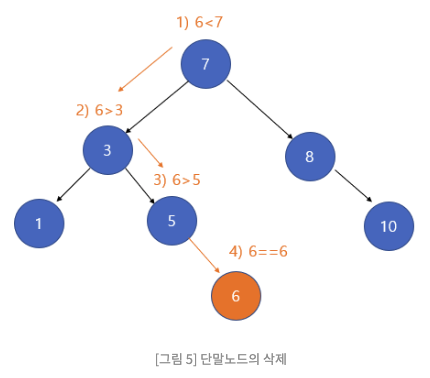
자식이 없는 단말노드의 삭제는 간단하다. 삭제할 노드의 부모 노드가 있다면 부모 노드의 자식 노드를 NULL로 만들고, 삭제할 노드를 삭제(메모리 해제) 해주면 된다.

2. 삭제하려는 노드의 서브 트리가 하나인 경우(왼쪽 혹은 오른쪽 서브 트리)

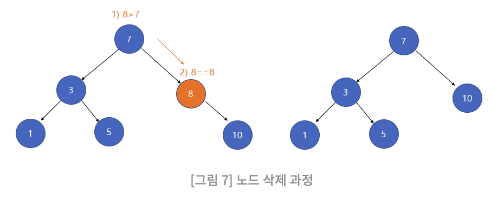
삭제하려는 노드의 서브 트리가 하나인 경우도 간단하다. 삭제할 노드의 자식노드를 삭제할 노드의 부모노드가 가리키게 하고 해당 노드를 삭제하면 된다. 

3. 삭제하려는 노드의 서브 트리가 두 개인 경우

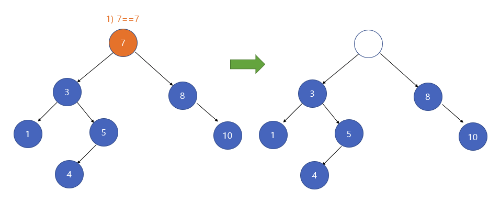
삭제하려는 노드의 서브트리가 두 개인 경우는 가장 복잡하다. 이 경우 두 가지 방법을 사용할 수 있다.

1) 삭제할 노드 왼쪽 서브 트리의 가장 큰 자손을 해당 노드의 자리에 올린다.

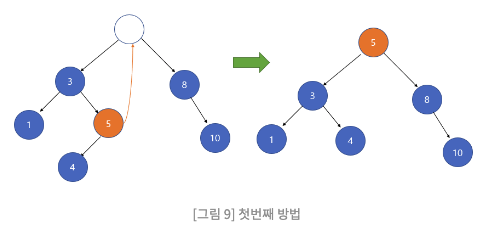
위와 같이 삭제할 노드의 왼쪽 서브 트리에서 가장 큰 자손을 해당 노드의 자리에 올리면, 이진 탐색 트리의 조건을 만족하면서 트리가 유지되는 것을 확인할 수 있다. 또한 자리를 옮기면서 다른 노드들(4번노드)도 자리가 적절히 이동한 것을 확인 할 수 있다.

2) 삭제할 노드 오른쪽 서브 트리의 가장 작은 자손을 해당 노드의 자리에 올린다.

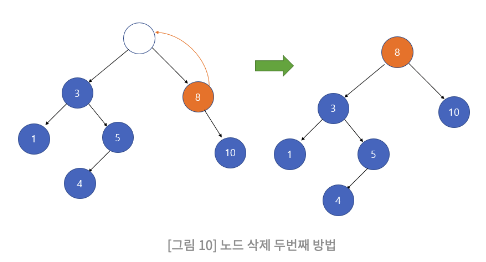
위와 같이 삭제할 노드의 오른쪽 서브 트리에서 가장 작은 자손을 해당 노드의 자리에 올리면, 이진 탐색 트리의 조건을 만족하면서 트리가 유지되는 것을 확인할 수 있다. 또한 자리를 옮기면서 다른 노드들(10번노드)도 자리가 적절히 이동한 것을 확인 할 수 있다.

이진 탐색 트리 vs 힙

---

공통점

• 둘 다 이진 트리이다.

차이점

📕 힙(Heap)

• 힙 : 각 노드의 값이 자식 노드보다 크거나 같다.(or 작거나 같다.)
  • 최대 힙 : 최대 값 최상단 root Node
  • 최소 힙 : 최소 값 최상단 root Node
• 중복을 허용한다.

힙 자료구조 : 최대값, 최소값을 빠르게 검색하기 위한 구조

📘 이진탐색트리(Binary Search Tree)

• 이진탐색트리 : 부모노드를 중심으로 부모노드보다 작으면 왼쪽 자식 노드로, 크면 오른쪽 자식노드로 배치
  • 좌 자식노드 < 부모 노드 < 우 자식 노드
• 중복을 허용하지 않는다.

  이진탐색트리 자료구조 : 특정 트리를 빠르게 탐색하기 위한 구조