🌿 신경망

퍼셉트론에서 가중치를 설정하는 작업은 여전히 사람이 수동으로 해야했음
→ 신경망은 가중치 매개변수의 적절한 값을 데이터로부터 자동으로 학습

아래 그림은 신경망의 예시 중 하나이다.

---

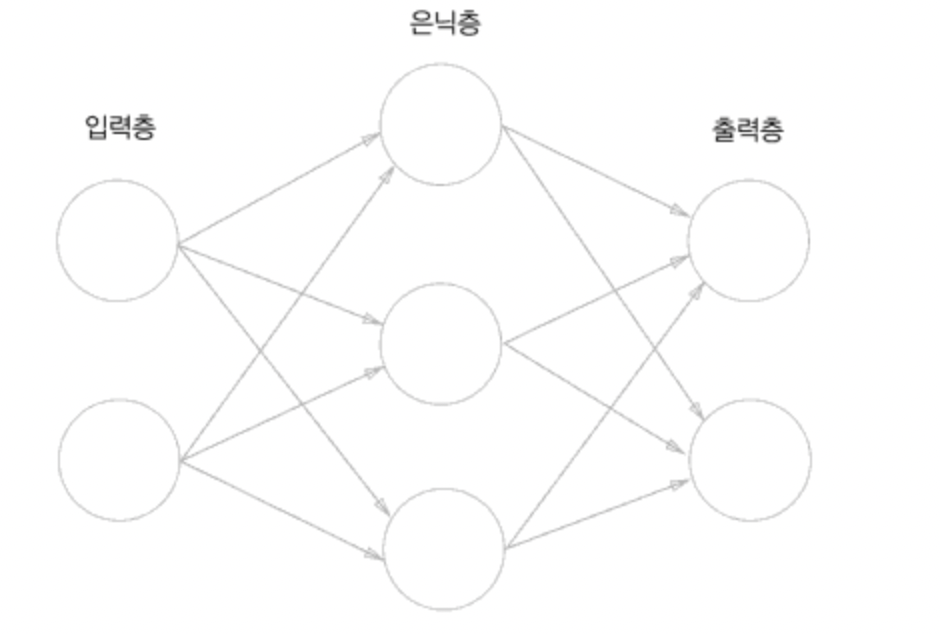
활성화 함수

activation function

입력 신호의 총합을 출력 신호로 변환하는 함수
입력 신호의 총합이 활성화를 일으키는지를 정하는 역할을 함

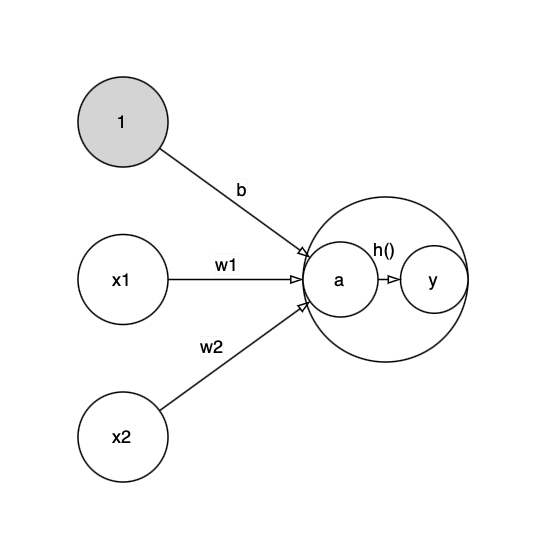
가중치 신호를 조합하여 a라는 노드가 되고, 활성화 함수 h()를 통과하여 y라는 노드로 변환된다.

📍 시그모이드 함수

sigmoid function

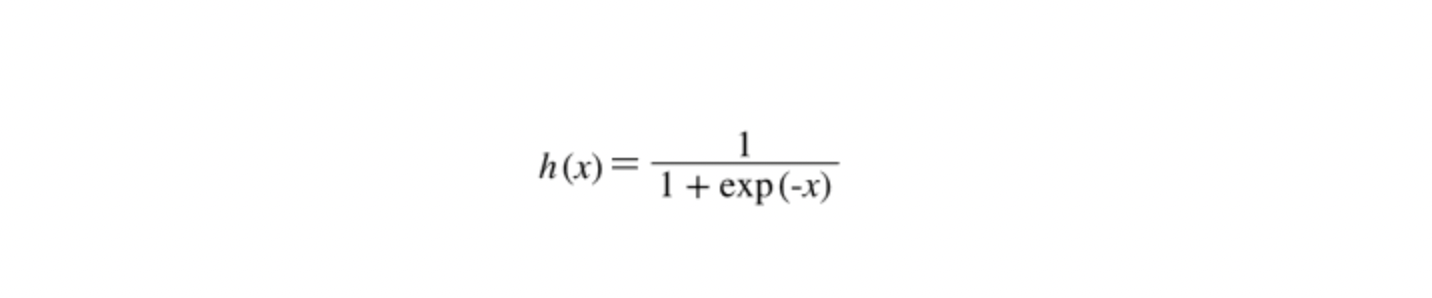
exp(-x)는 e^{-x}를 뜻하며, e는 자연상수로 2.7182... 의 값을 갖는 실수

신경망에서는 활성화 함수로 시그모이드 함수를 이용해 신호를 변환하고, 그 변환된 신호를 다음 뉴런에 전달함

시그모이드 함수는 다음과 같이 구현이 가능하다.

def sigmoid(x):
    return 1 / (1 + np.exp(-x))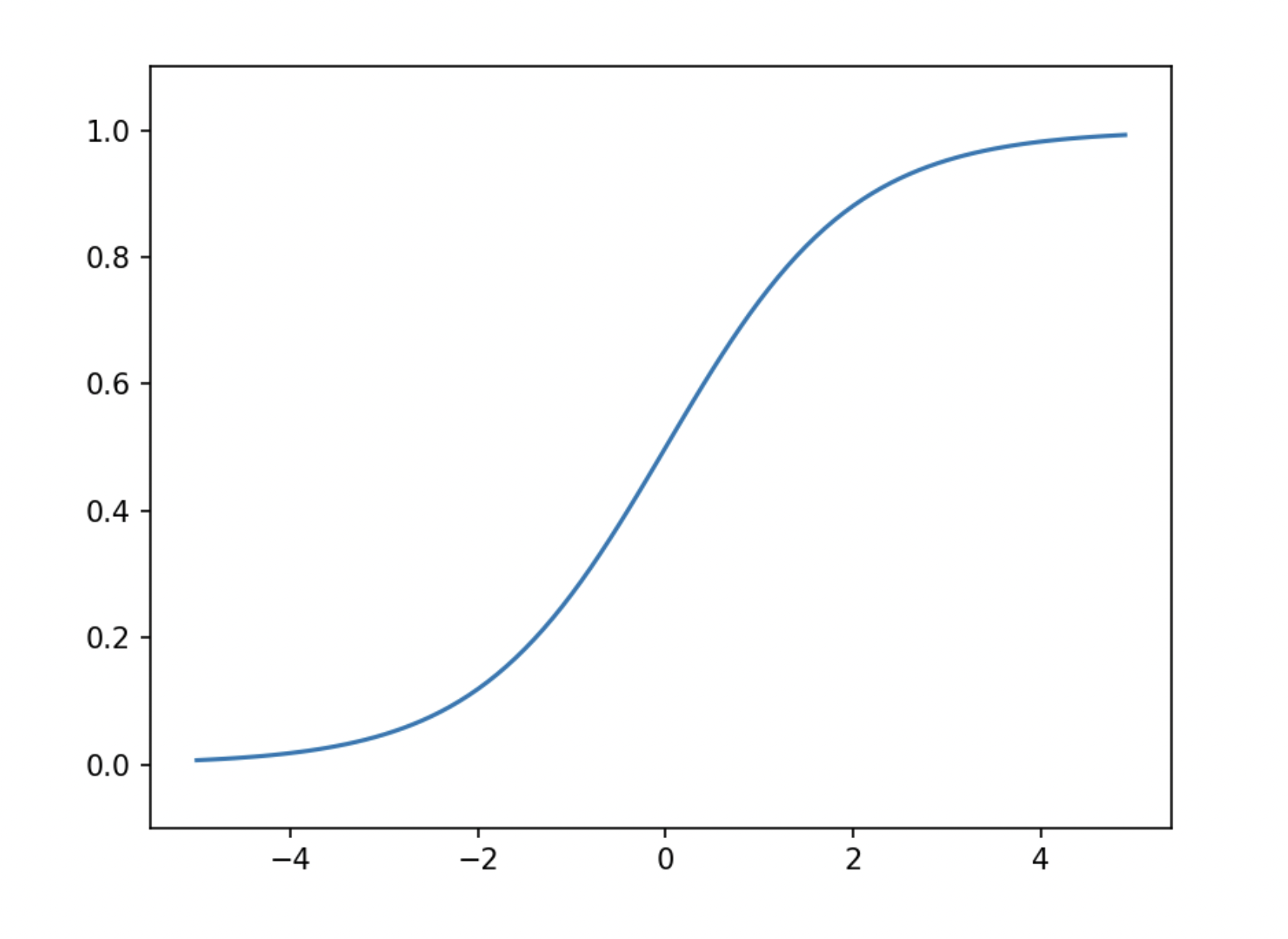

📍 계단 함수

step function
계단 함수는 입력이 0을 넘으면 1을 출력하고, 그 외에는 0을 출력

def step_function(x):
    if x > 0:
        return 1
    else:
        return 0

넘파일 배열도 지원하도록 코드를 수정하면 다음과 같다.

def step_function(x):
    y = x > 0
    return y.astype(np.int)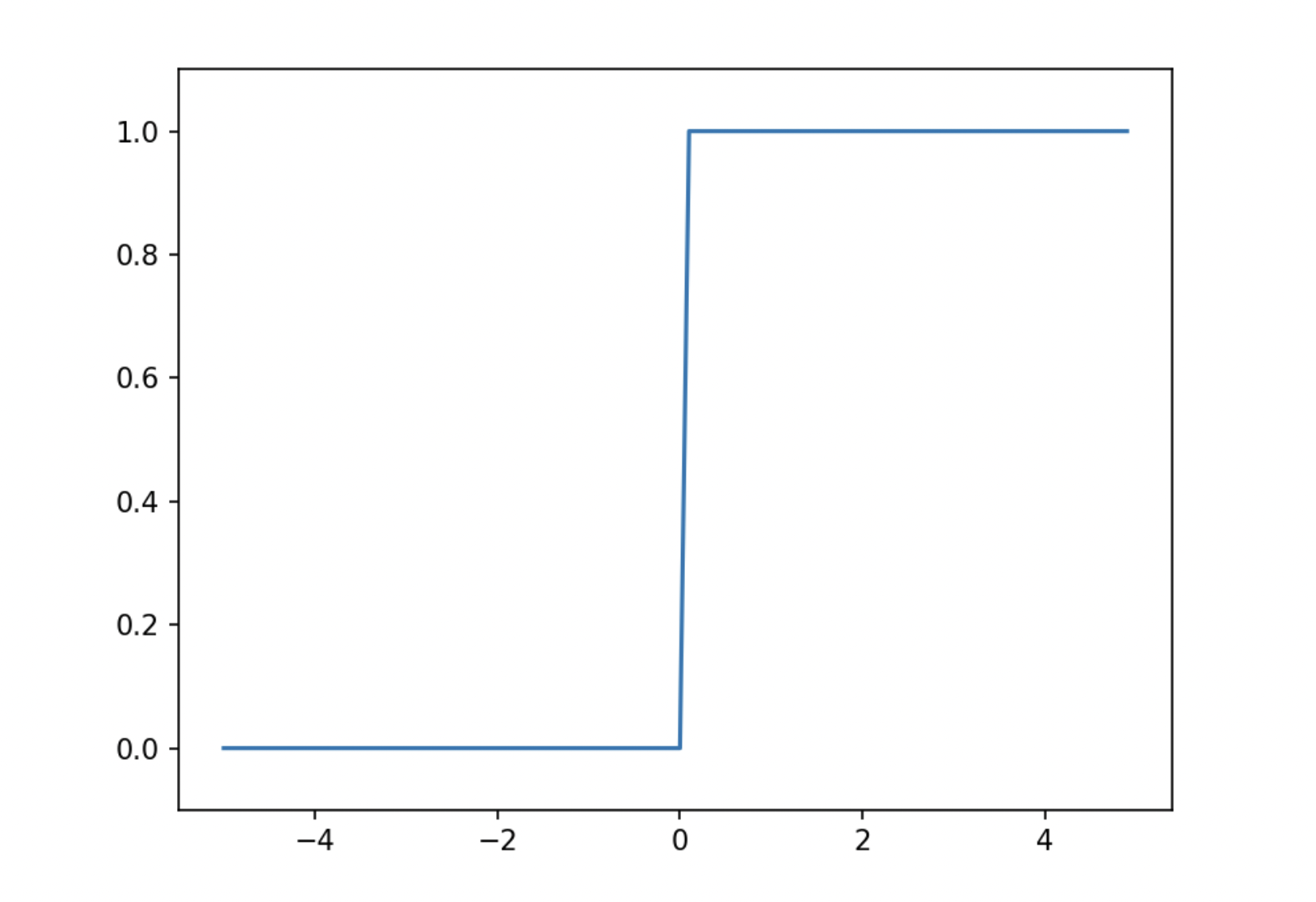

시그모이드 함수와 계단함수

• 공통점
  • 입력이 작을 때 출력이 0에 가깝고, 입력이 커지면 출력이 1에 가까움
  • 비선형 함수
• 차이점
  • 시그모이드 함수는 출력이 연속적으로 변하는 반면 계단 함수는 0을 경계로 출력이 급하게 변함

** 선형 함수를 이용하면 신경망 층을 깊게 하는 의미가 사라지므로 신경망에서는 활성화 함수로 비선형 함수를 사용해야 함

📍 ReLU 함수

입력이 0을 넘으면 그 입력을 그대로 출력, 0 이하이면 0을 출력하는 함수

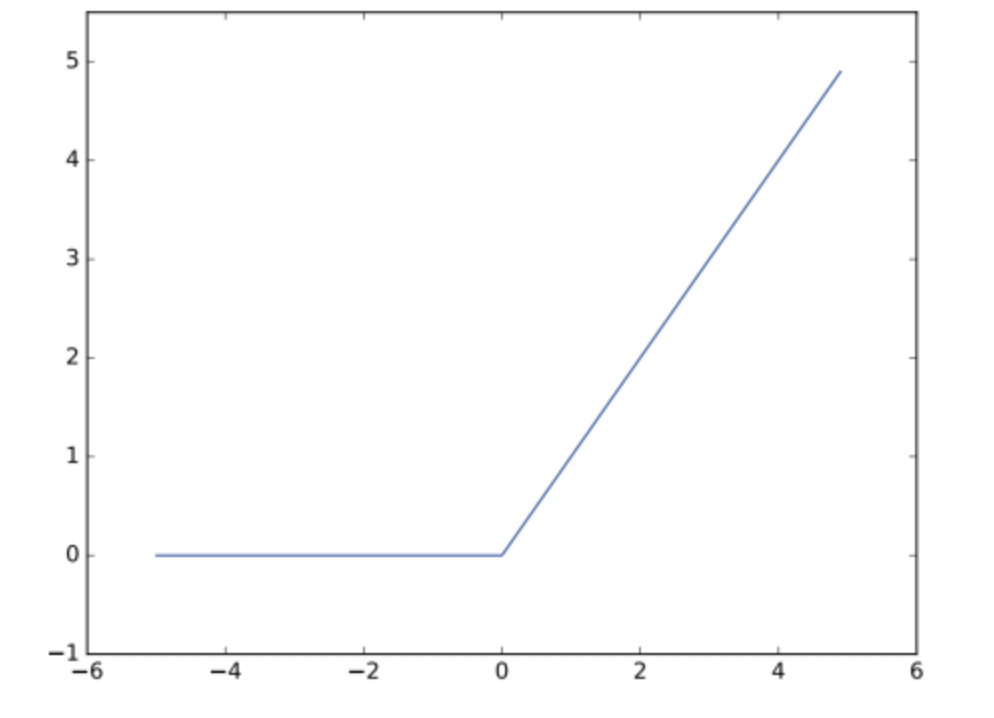
ReLU 함수는 다음과 같이 구현할 수 있다.

def relu(x):
    return np.maximum(0, x)

---

3층 신경망의 구현

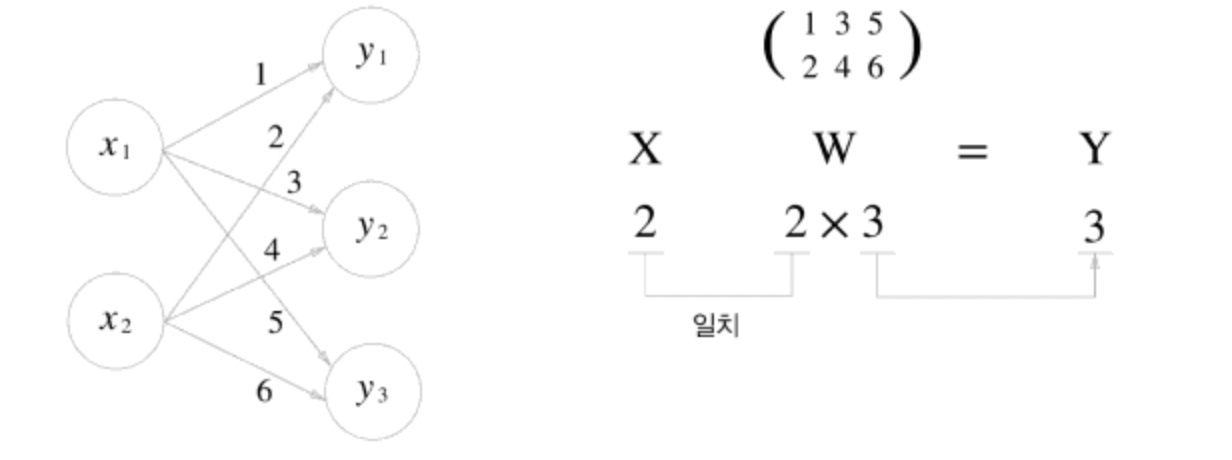
행렬 곱을 활용하여 3층 신경망을 구현해보자

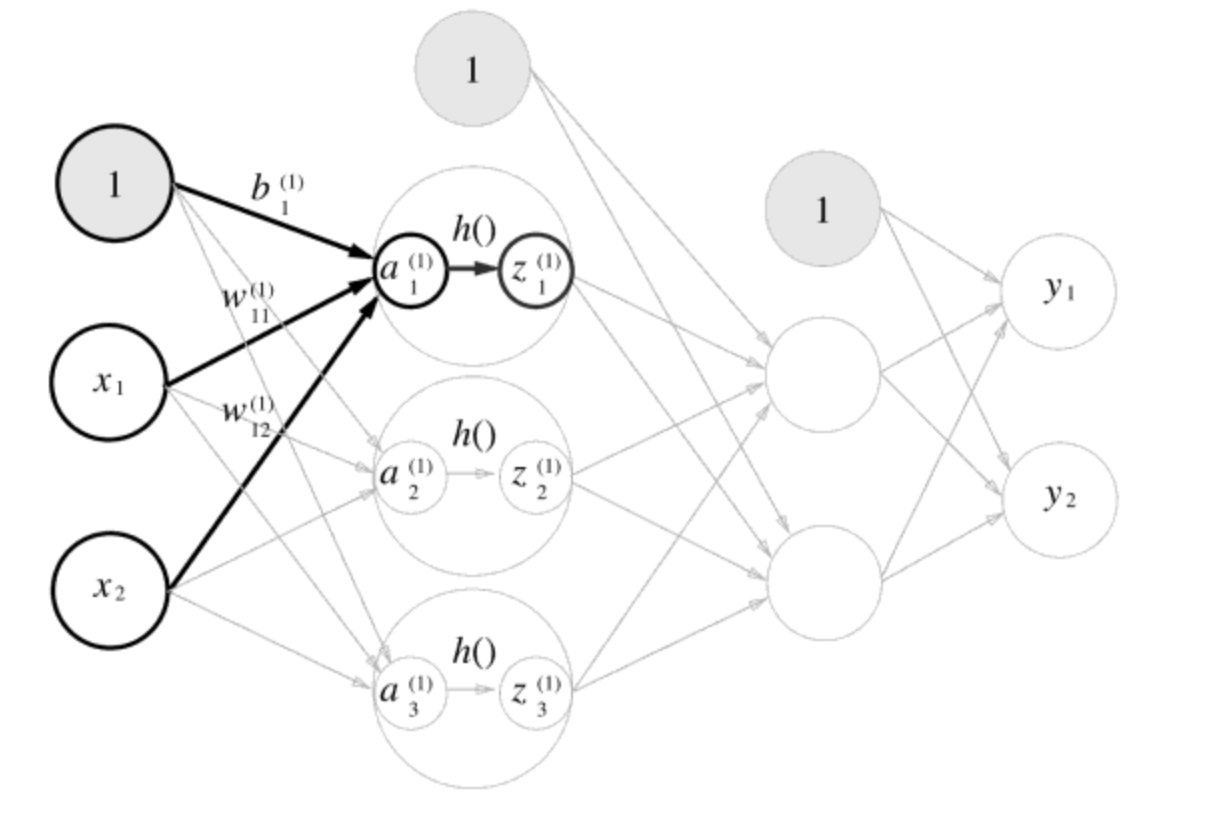
입력층에서 1층으로의 신호 전달은 다음과 같다

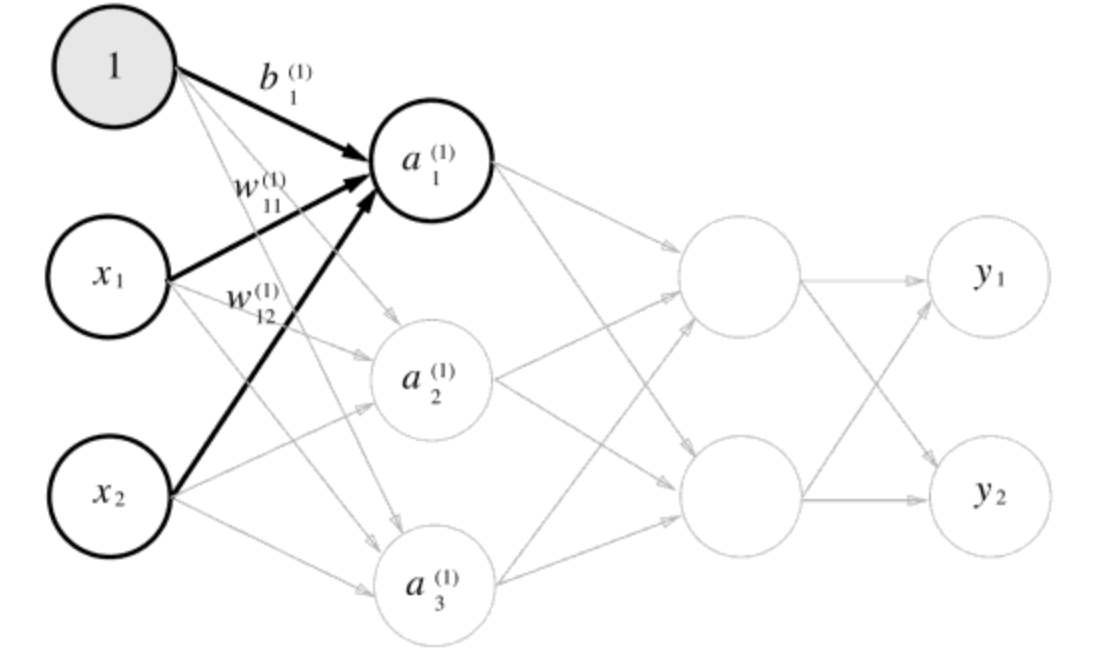
가중치를 곱한 신호 2개와 편향을 합해서 계산한 값으로, a1 = w11x1 + w12x2 + b1 과 같이 계산된다.

행렬 곱을 활용하면 1층의 가중치 부분을 A = XW + B 처럼 간소화할 수 있다.

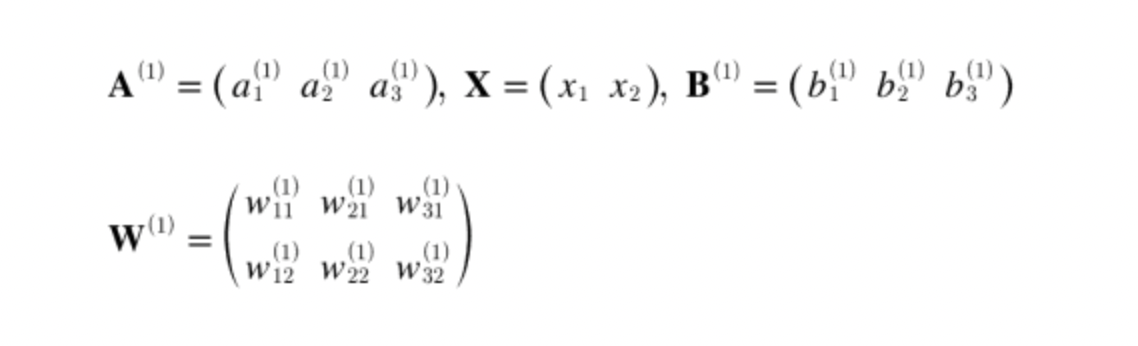
이는 다음과 같이 구현이 가능하다.

import numpy as np

X = np.array([1.0,0.5])
W1 = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
B1 = np.array([0.1,0.2,0.3])

A1 = np.dot(X,W1) + B1
print(A1)

그 다음으로 1층에서의 활성화 함수를 살펴보자.

여기에서는 활성화 함수로 시그모이드 함수를 사용한다고 하면 구현은 다음과 같다.

Z1 = sigmoid(A1)

print(A1) # [0.3, 0.7, 1.1]
print(Z1) # [0.55444252, 0.66818777, 0.75026011]

1층에서 2층으로 가는 과정은 앞에서와 비슷하게 진행된다.

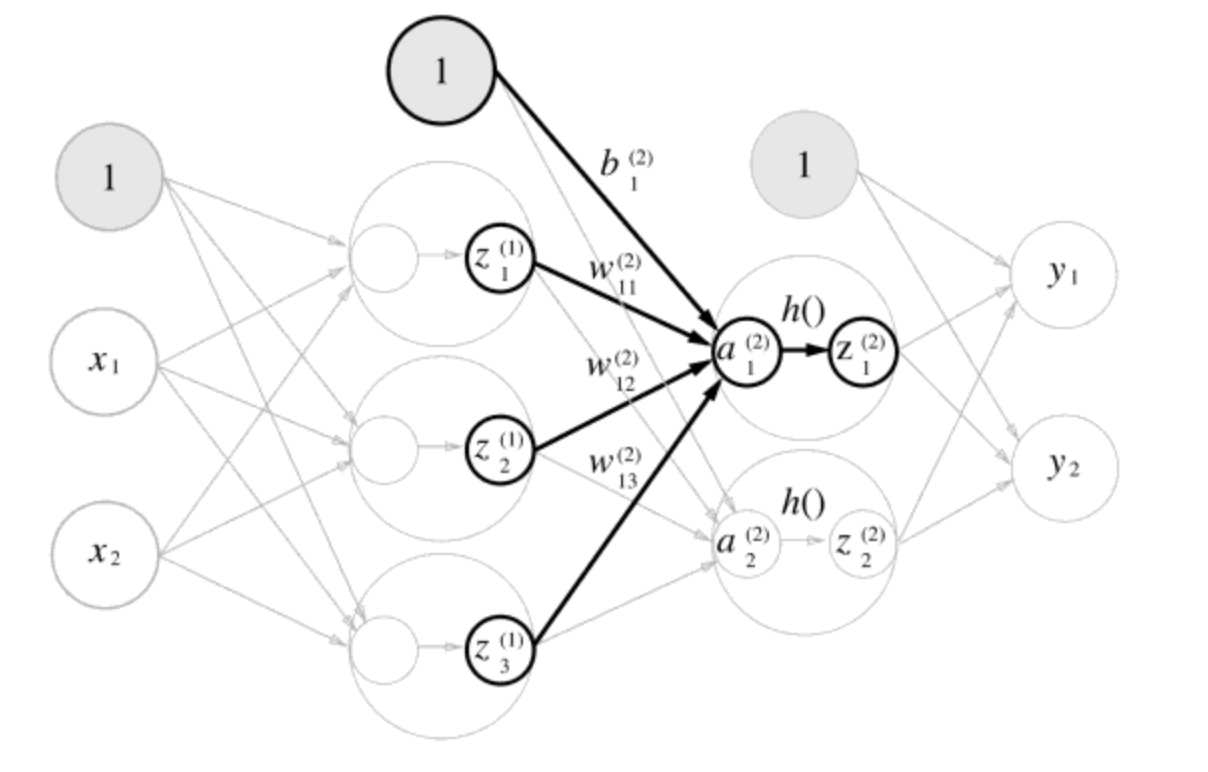
W2 = np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])
B2 = np.array([0.1,0.2])

print(Z1.shape) # (3, )
print(W2.shape) # (3, 2)
print(B2.shape) # (2, )

A2 = np.dot(Z1, W2) + B2
Z2 = sigmoid(A2)

마지막으로 2층에서 출력층으로의 신호 전달을 살펴보자.
출력층도 그동안의 구현과 거의 같은데, 활성화 함수만 지금까지의 은닉층과 다르다.

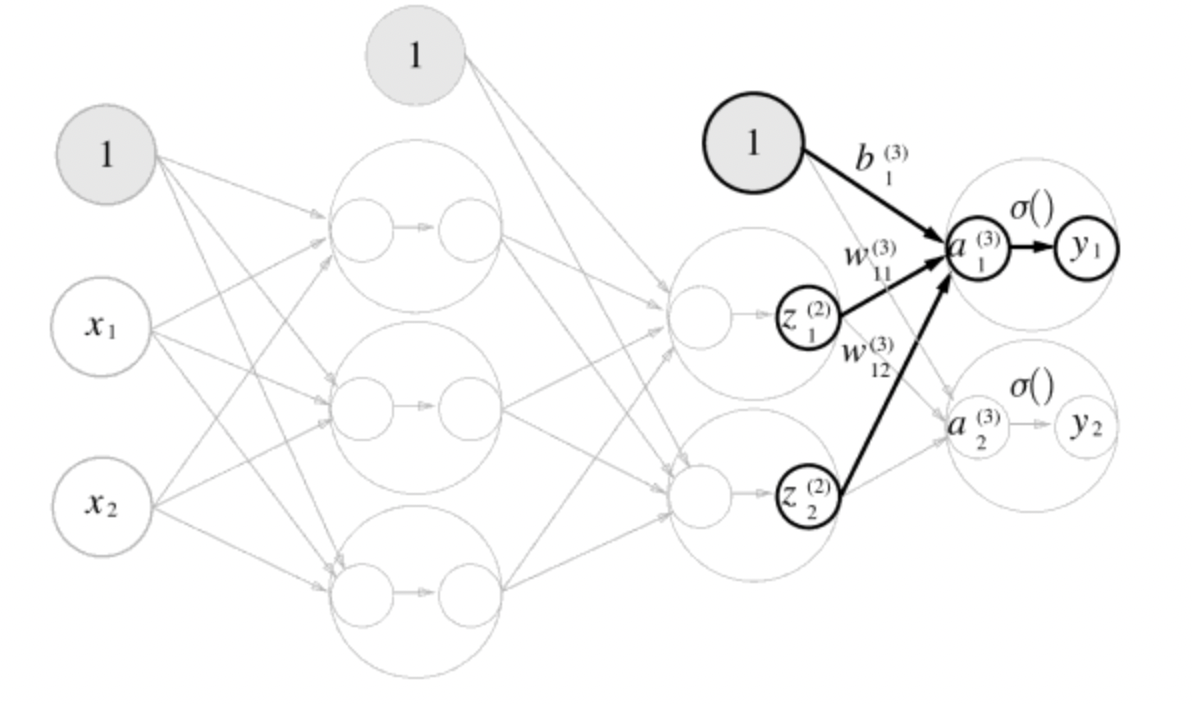
def identity_function(x):
	return x
    
W3 = np.array([[0.1,0.3],[0.2,0.4]])
B3 = np.array([0.1,0.2])

A3 = np.dot(Z2, W3) + B3
Y = identity_function(A3) # 혹은 Y = A3

여기서는 항등 함수인 identity_function()을 정의하고, 이를 출력층의 활성화 함수로 이용했다.

출력층의 활성화 함수는 문제의 성질에 맞게 정함
일반적인 활성화 함수 사용은 다음과 같다.

• 회귀 → 항등 함수
• 2클래스 분류 → 시그모이드 함수
• 다중 클래스 분류 → 소프트맥스 함수

위의 구현을 최종 정리하면 3층 신경망 구현은 다음과 같다.

from sigmoid import sigmoid
from identity_function import identity_function
import numpy as np

def init_network():
    network = {}
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
    network['b1'] = np.array([0.1, 0.2, 0.3])
    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
    network['b2'] = np.array([0.1, 0.2])
    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
    network['b3'] = np.array([0.1, 0.2])

    return network

def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    # input Layer -> Layer 1
    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    # Layer 1 -> Layer 2
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    # Layer 2 -> Output Layer
    a3 = np.dot(z2, W3) + b3
    y = identity_function(a3)

    return y

network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y)