💡 학습이란?
훈련 데이터로부터 가중치 매개변수의 최적값을 자동으로 획득하는 것
신경망이 학습할 수 있도록 해주는 지표에는 손실함수가 있다
학습의 목표 : 손실 함수의 결괏값을 가장 작게 만드는 가중치 매개변수를 찾는 것
데이터로부터의 학습
신경망의 특징은 데이터를 보고 학습할 수 있다는 점
즉, 가중치 매개변수의 값을 데이터를 보고 자동으로 결정한다는 의미
이는 기존 기계학습에서 사용하던 방법보다 사람의 개입을 더욱 배제할 수 있도록 해주는 중요한 특성
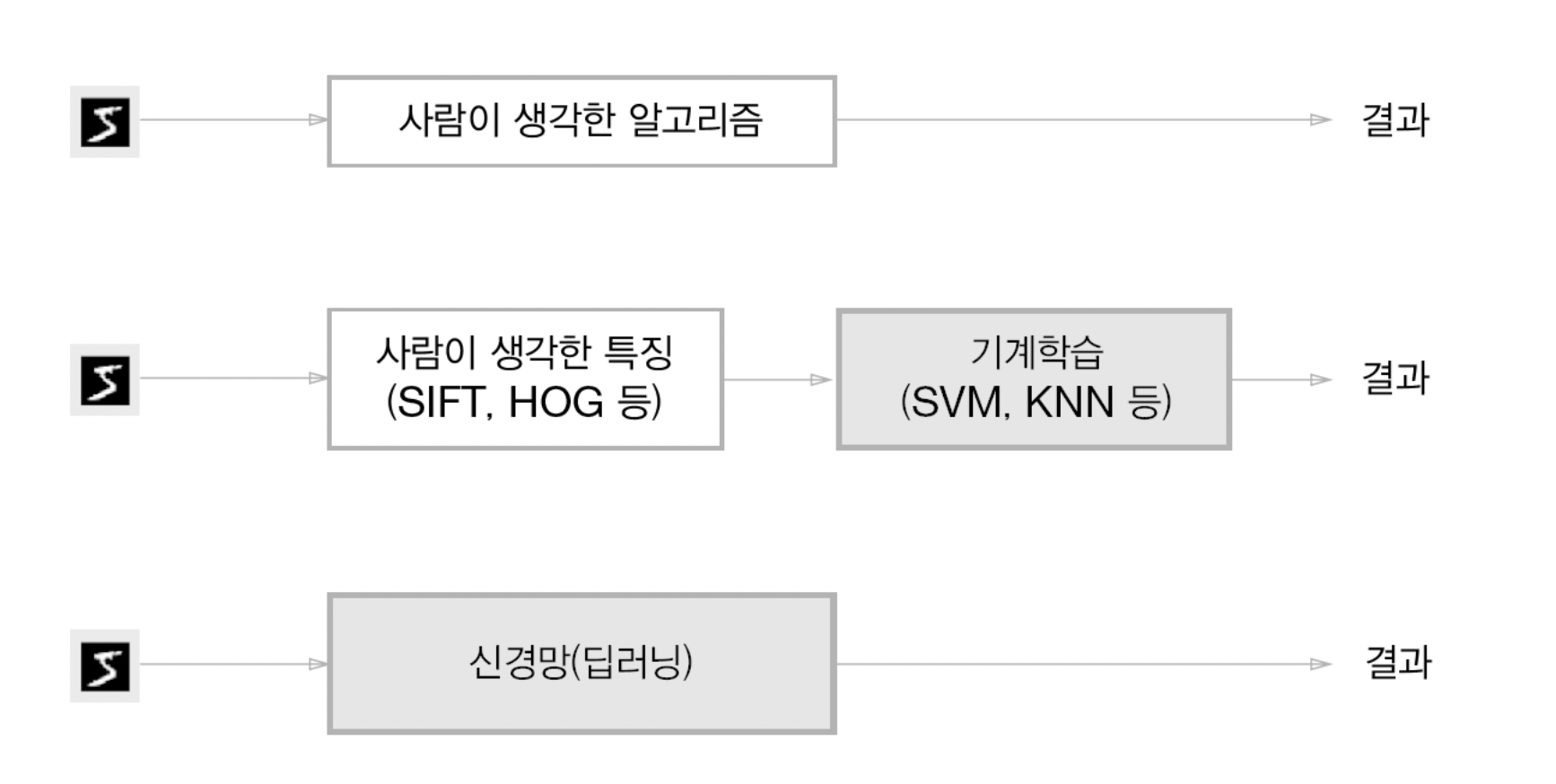
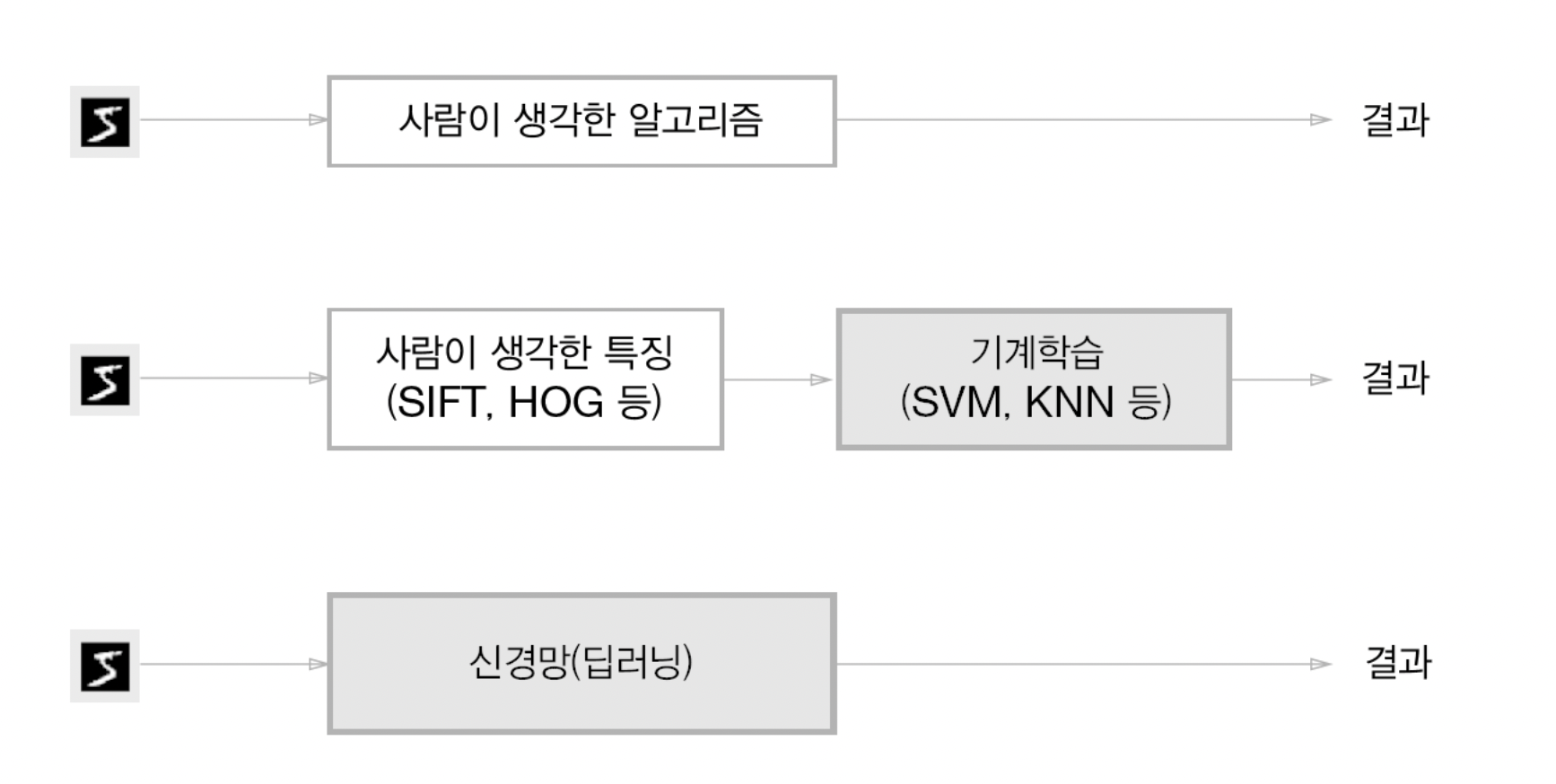
신경망은 위와 같이 이미지를 있는 그대로 학습
두 번째 접근 방식(특징과 기계학습 방식)은 특징을 사람이 설계하지만, 신경망은 이미지에 포함된 중요 특성까지도 기계가 스스로 학습
신경망은 주어진 데이터 그 자체를 학습하기 때문에 모든 문제를 같은 맥락에서 풀 수 있다는 이점이 있다.
훈련 데이터와 시험 데이터
기계 학습 문제는 데이터를 주로 훈련 데이터(train data)와 시험 데이터(test data)로 나눠 학습과 실험을 수행
- 훈련 데이터만 사용해 학습하면서 최적의 매개변수를 찾음
- 그 다음 시험 데이터를 사용하여 앞서 훈련한 모델의 실력을 평가
나눠야 하는 이유?
범용적으로 사용할 수 있는 모델을 만들기 위해 !
일부 데이터셋에만 지나치게 최적화된 상태인 오버피팅을 방지
손실 함수
신경망 학습에서 사용하는 지표 (신경망 성능의 '나쁨' 을 나타냄)
일반적으로 오차제곱합과 교차 엔트로피 오차를 사용
📍 오차제곱합
sum of squares for error, SSE
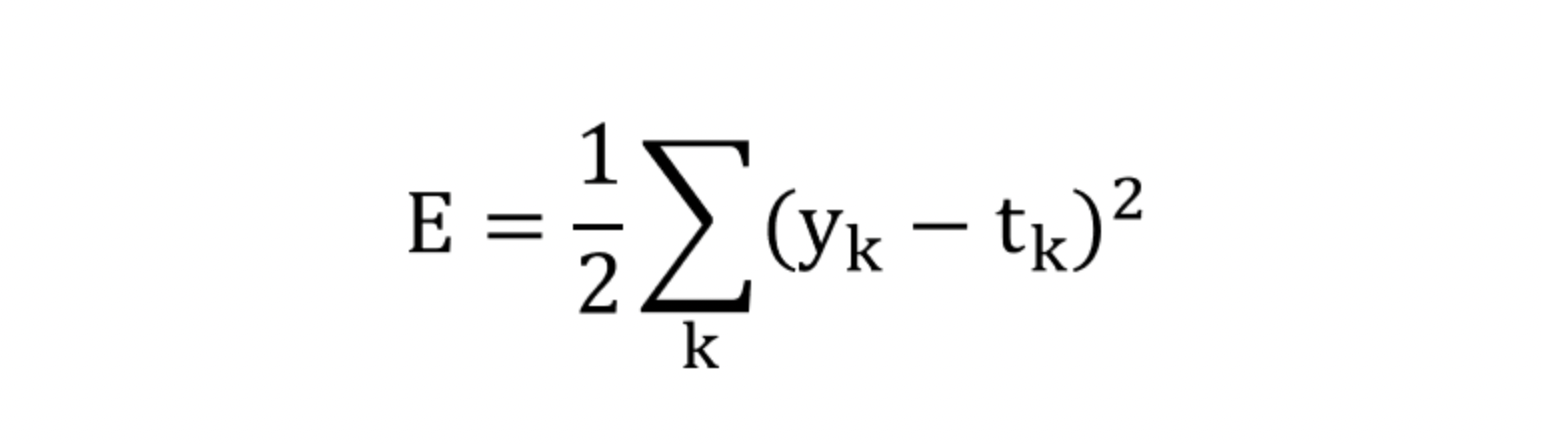
y_k : 신경망의 출력 (신경망의 추정 값)
t_k : 정답 레이블
k : 데이터의 차원 수
신경망의 출력인 y_k는 소프트맥스 함수의 출력으로써, 각 클래스에 대한 확률 값을 가지고,
t_k는 정답 클래스에 대해서만 1, 나머지는 0의 값을 갖는 원-핫 인코딩된 정답 레이블이다.
ex)
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]오차제곱합의 구현은 다음과 같다.
def sum_squares_error(y, t):
return 0.5 * np.sum((y-t)**2)
위의 예시의 경우 오차제곱합 기준으로 첫 번째 추정 결과가 정답에 더 가까울 것으로 판단할 수 있다.
📍 교차 엔트로피 오차
cross entropy error, CEE
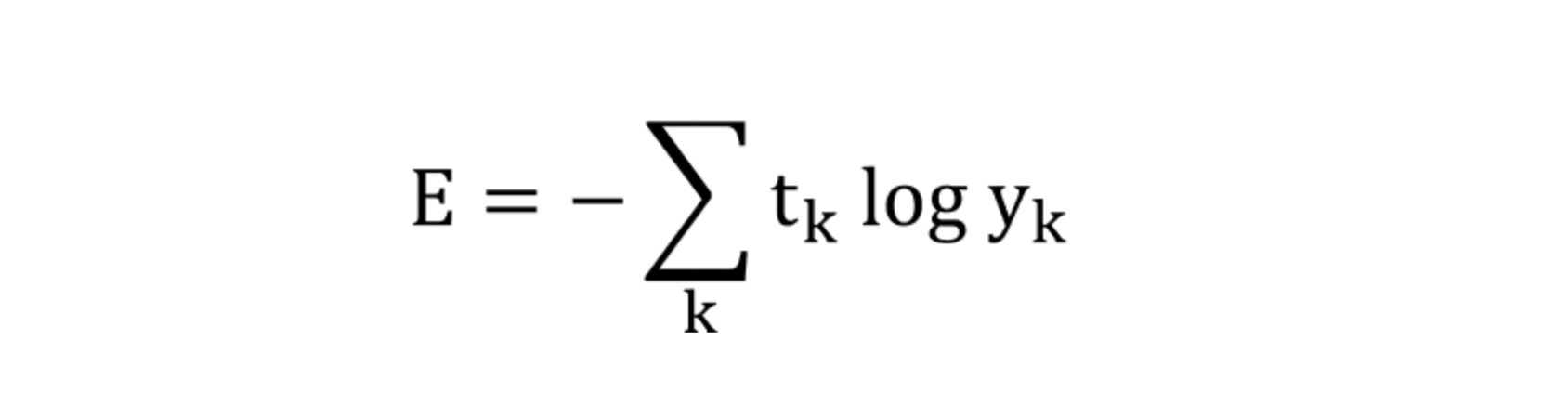
log는 밑이 e인 자연로그
t_k는 정답에 해당하는 인덱스의 원소만 1이고 나머지는 0인 원-핫 인코딩된 값이기 때문에 실질적으로 정답일 때의 추정(t_k가 1일 때의 y_k)의 자연로그를 계산하는 것과 같은 식이 된다.
즉, 교차 엔트로피 오차는 정답일 때의 출력이 전체 값을 결정
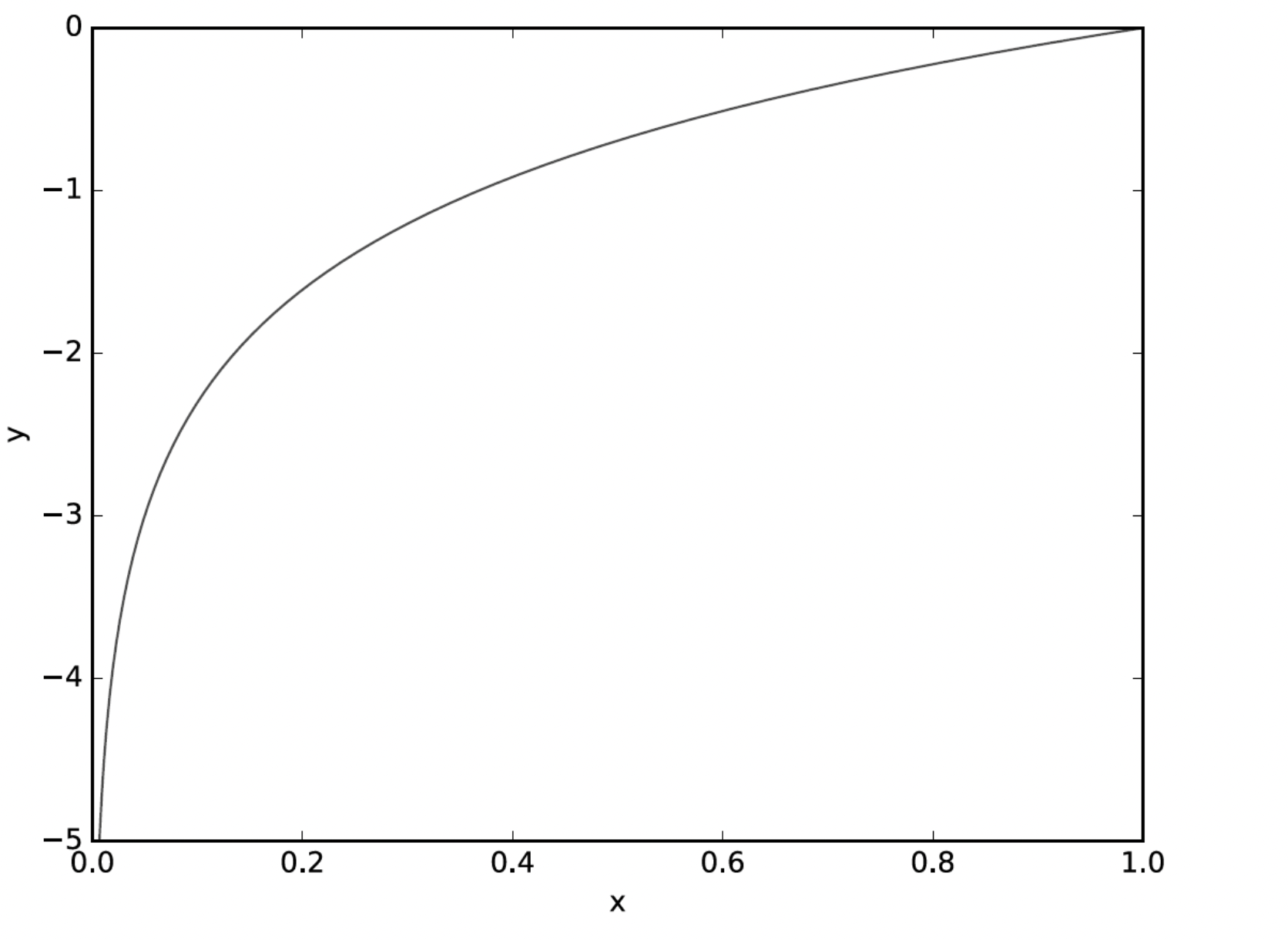
위의 함수는 y = log(x) 그래프이다.
그래프를 통해 알 수 있듯이 교차 엔트로피 오차 식의 값은 정답에 해당하는 출력이 커질수록 0에 다가가다가, 그 출력이 1일 때 0이 된다.
반대로 정답일 때의 출력이 작아질수록 오차는 커지게 된다.
구현은 다음과 같다.
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta))delta라는 작은 값을 더해주어 y가 0이 되어도 -inf(마이너스 무한대)가 발생하지 않도록 한다.

교차 엔트로피 오차 함수도 결과(오차 값)가 더 작은 첫 번째 추정이 정답일 가능성이 높다고 판단
미니배치 학습
많은 데이터를 처리하기 위해 훈련 데이터 모두에 대해 손실 함수의 합을 구하는 방법이 필요
예를 들어 교차 엔트로피 오차는 다음과 같이 수정할 수 있다.
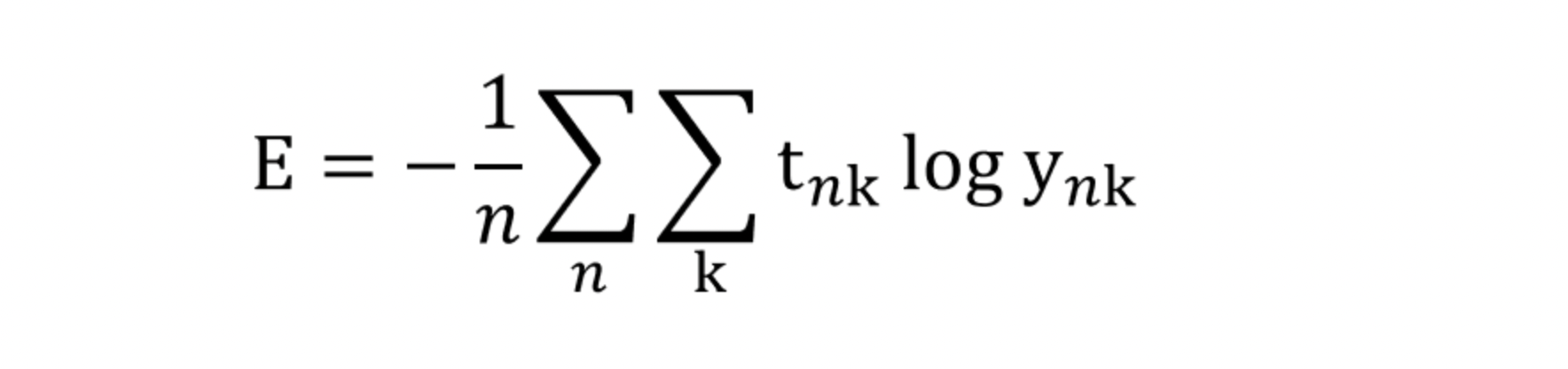
하나의 데이터에 대한 손실함수를 N개의 데이터로 확장하고 마지막에 N으로 나누어 정규화한 식이다.
→ 평균 손실 함수
하지만 모든 데이터의 값을 훑으며 손실 함수의 합을 구하는 것은 비효율적
이런 경우 데이터 일부를 추려 전체의 '근사치'로 이용하고, 이 일부를 미니배치(mini-batch)라고 함
배치용 교차 엔트로피 오차 구현
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(t*np.log(y+1e-7)) / batch_sizey가 1차원이면 reshape로 데이터 형상을 바꿔 동일하게 처리할 수 있도록 해줌
정답 레이블이 원-핫 인코딩이 아닌 '2', '7' 등의 숫자 레이블인 경우 다음과 같이 구현이 가능하다.
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(t*np.log(y[np.arange(batch_size), t]+1e-7)) / batch_size✅ 손실 함수의 필요성
'정확도'라는 지표 대신 '손실 함수의 값'이라는 우회적인 방법을 택하는 이유는?
→ '미분'의 역할에 주목
신경망 학습에서는 최적의 매개변수 탐색 시 매개변수의 미분 값을 단서로 서서히 갱신
정확도의 경우 미분 값이 대부분의 장소에서 0이 되어 매개변수를 갱신할 수 없으므로 사용이 불가
정확도는 손실 함수에 비해 비교적 불연속적 → 미분으로의 매개변수 갱신의 어려움
