[알고리즘] 시간복잡도(Time Complexity)와 Big-O표기법(Big-O Notation)

Kyunghwan Ko·2021년 9월 28일

알고리즘

목록 보기

2/9

인트로

웹앱프로젝트를 진행하고 있지만 알고리즘관련 공부를 너무 등한시한 것 같아서 알고리즘 관련된 공부도 병행해서 진행해보려하고 관련내용을 블로그에 정리할 것입니다. 이에 앞서 알고리즘 공부시작할때 반드시 알아야할 개념들에 대해 설명드리겠습니다.(Python 3 기반)

1. 자료구조와 알고리즘

알고리즘(Algorithm)은

문제의 입력(input)을 수학적이고 논리적으로 정의된 연산과정을 거쳐 원하는 출력(output)으로 변환/계산(Computation)하는 절차이고, 이 절차를 C나 Python과 같은 언어로 표현하면 프로그램(Program)또는 코드(Code)가 됩니다.

알고리즘이 되기 위한 필수조건

※ 아래의 조건을 어긴다면 알고리즘이라고 할 수 없다.

모든입력에 대해 올바른 답을 출력해야함
합리적인 시간안에 답을 출력해야함

자료구조(Data Structure)은

쉽게 말해 데이터를 담는 그릇(Data Container)라고 할 수 있습니다.

자료구조의 종류는 배열(Array(in C) 또는 List(in Python)), 연결리스트(Linked-List), 트리(Tree), 해시테이블(Hash Table), 그래프(Graph)등이 있습니다.

따라서 자료구조와 알고리즘의 관계를 정리하면

입력은 자료의 접근과 수정이 빠른 자료구조에 저장되고

자료구조에 저장된 입력 값을 기본적인 연산(Primitive Operation)을 차례로 적용하여 원하는 출력을 계산하는 절차가 알고리즘입니다.

2. 가상컴퓨터, 가상언어, 가상코드 + 기본연산

공학자(Engineer)들은 항상 효율적이고 완벽한 최적의(optiaml) 프로그램을 구현하길 갈망하는 것 같습니다.

그로인해 프로그램을 구현할때 자료구조와 알고리즘의 성능을 파악해야하는대 그때의 지표로써
프로그램의 수행시간(시간복잡도)을 많이 사용합니다.

이를 위해 실제 코드(C, Python, Java등)로 구현하여 실제 컴퓨터에서 실행한 후, 수행시간을 측정할 수도 있지만, HW/SW 환경을 하나로 통일해야하는 어려움이 있습니다.
따라서 가상언어로 작성된 가상코드를 가상컴퓨터에서 시뮬레이션하여 HW/SW에 독립적인 계산 환경(Computational Model)에서 측정해야 합니다.

가상컴퓨터(Virtual Machine)

현대 컴퓨터 구조는 튜링머신(Turing Machine)에 기초한 폰 노이만(von Neumann)구조를 따릅니다. 그리고 현재 가장 많이 사용하는 현실적인 가상 컴퓨터 모델은 RAM(Random Access Machine) 모델입니다.

RAM모델은 CPU + 메모리(Memory) + 레지스터(Register) + 기본연산(Primitive Operation)으로 정의합니다.

CPU는 연산(operation, command)을 실질적으로 수행하는 것입니다.

Memory는 임의의 크기를 가진 실수 (즉, 정확한 실수 값을) 저장할 수 있는 무한한 워드(word)로 구성됩니다.

Register는 CPU의 계산에 활용되는 저장장치로써 일종의 메모리입니다.

기본연산은 단위 시간에 수행할 수 있는 연산을 의미합니다.

기본연산

1. 대입 또는 복사 연산:

ex. a = b, b의 값을 a 레지스터에 복사 또는 b 레지스터의 값을 a 메모리에 복사

-> b의 값을 읽고(Read) a에 쓰다(Write). 두 과정이지만 단위시간에 시행할 수 있다고 봅니다.

2. 산술연산:

+, -, *, / (나머지 % 연산은 허용안되나 본 블로그 작성시 기본연산으로 포함하겠음.)

추가적으로 버림, 올림, 반올림 연산을 포함

->레지스터에 복사된 값에 대해 기본연산을 수행

3. 비교연산:

>, >=, <, <=, ==, !=

ex. a > b 는 사실 a - b > 0 이므로 이 역시 기본연산으로 취급할 수 있다.

4. 논리연산:

AND, OR, NOT

5. 비트연산:

bit-AND, bit-OR, bit-NOT, bit-XOR, <<, >>

이러한 기본연산으로 정의한 가상컴퓨터를 RAM모델이라 하고,
우리는 앞으로 RAM모델 위에서 알고리즘의 수행시간을 측정해서 그 측정된 시간을 비교해서 성능을 평가할 것입니다.

※ Real RAM 모델은 root, 삼각함수, exp, log 함수 등도 단위시간에 수행된다고 가정하는 더 강력한 계산모델이다. 이 모델은 실수 연산이 중요한 기하 알고리즘의 계산ㅇ모델에서 주로 사용됩니다.(현대 컴퓨터와 프로그래밍 언어 모델에 가장 근접한 계산모델입니다.)

가상언어(Pseudo Language)

가상컴퓨터에서 프로그램을 수행하기 위해 필요한 것입니다.

영어나 한국어와 같은 실제언어보다 간단 명료하지만, C, Python 같은 프로그래밍 언어보다 융통성있는 언어로, Python 유사하게 정의함. (수학적/논리적 모호함없이 명령어가 정의되기만 하면 됨)

가상코드(Pseudo Code)

가상언어로 작성된 코드입니다.

실제 컴퓨터에서 돌아가는 코드는 아니고, 가상머신인 RAM모델에서 돌아가는 코드이므로 내용전달을 주 목적으로 합니다.

※ 본 블로그에서 가상언어와 가상코드를 많이 쓰진 않을 것이지만 개념적으로 알아두면 좋을 것 같습니다.

기본연산에 대해 자세히 아는것이 중요합니다.

시간복잡도(Time Complexity)

가상컴퓨터에서 가상언어로 작성된 가상코드를 실행한다고 가정합니다.

특정입력에 대해 수행되는 알고리즘의 기본연산의 횟수로 수행시간을 정의합니다.

프로그램의 수행시간을 완벽하게 알기위해선 모든 입력에대해 수행시간을 구한다음 평균을 구하는 것입니다.

하지만 문제는 입력의 종류가 무한하므로 모든 입력에 대해 수행시간을 측정하는 것이 현실적으로 가능하지 않습니다.

따라서 최악의 경우의 입력을 가정하여, 최악의 경우의 입력(Worst-Case input)에 대한 알괴즘의 수행시간을 측정합니다.

※ 알고리즘의 수행시간 = 최악의 경우의 입력에 대한 기본연산의 수행횟수

최악의 경우의 수행시간은 입력의 크기 n에 대한 함수 T(n)으로 표현합니다.

T(n)의 수행시간을 갖는 알고리즘은 어떠한 입력에 대해서도 T(n) 시간 이내에 종료됨을 보장합니다.

실시간 제어가 필요하고 절대안전이 요구되는 분야(항공, 교통, 위성, 원자로 제어 등)에선 실제로 최악의 경우를 가정한 알고리즘 설계가 필요하기 때문에, 유효한 수행시간 측정방법이라고 볼 수 있습니다.

따라서 앞으로 프로그램의 수행시간을 파악할땐,

최악의 경우의 입력에 대해, 알고리즘의 기본연산(대입, 산술, 비교, 논리, 비트논리)의 횟수를 세면됩니다.

Big-O표기법

알고리즘의 성능을 수학적으로 표현해주는 표기법입니다.
알고리즘의 시간복잡도, 공간복잡도를 표현할 수 있습니다다.
알고리즘의 실제 수행시간을 표기한다기 보다
데이터나 사용자의 증가율에 따른 알고리즘의 성능을 예측하는게 목표이므로 상수의 경우 모두 1로 취급합니다.
시간복잡도를 나타내는 T(n)에서 가장 영향력이 큰(dominant)값만을 나타냅니다.
(ex. T(n) = 2n^2 + n + 1일 경우, O(n^2)로 표현)
왜냐하면 n이 무한대로 증가한다고 가정할 경우 실질적으로 해당 실행시간에 영향을 주는 부분은 n^2이기 때문.

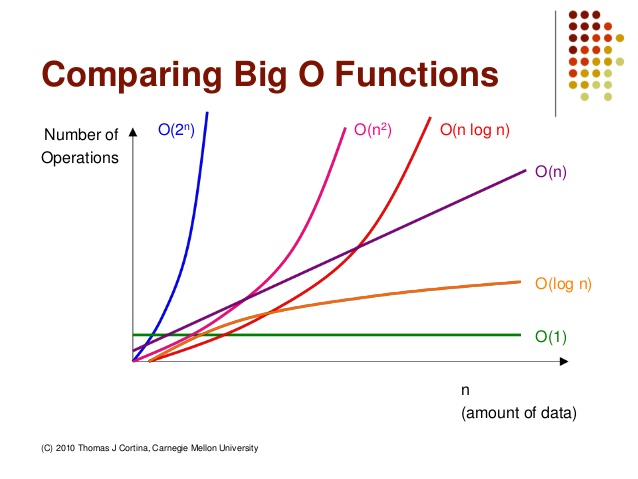
http://devwebcl.blogspot.com/2016/12/big-o-comparison.html

위 사진을 보듯이 O(n^2)나 O(2^n)같이 승으로 표현되는 알고리즘은 사실상 사용할 수 없는 알고리즘이라고 볼 수 있다. 하지만 추후에 포스팅되겠지만 대표적인 O(n^2) 케이스에 해당하는 버블정렬(Bubble Sort)알고리즘은 매우 가독성이 좋고 코드작성하기 편하기 때문에 자주 사용됩니다.

보편적으로 O(nlog n)이나 O(log n)의 복잡도를 가지는 알고리즘을 선호합니다.

Big-O표기법	복잡도	설명
O(1)	상수	실행시간은 입력의 크기에 관계없이 일정합니다. O(1)의 복잡도를 가지는 대표적인 경우는 해시테이블에서 요소를 찾는 것입니다.
O(n)	선형	실행시간은 입력의 크기에 따라 선형적으로 증가합니다. O(n)의 복잡도를 가지는 대표적인 경우는 리스트의 모든 원소에 대한 조건을 비교하는 함수입니다.
O(n^2)	제곱	실행시간은 입력 크기의 제곱함수입니다. O(n^2)의 복잡도를 가지는 대표적인 경우는 각 원소를 두번 확인해야하는 리스트에서 중복 값을 찾는 함수입니다.
O(2^n)	지수	실행시간은 입력의 크기에 따라 기하급수적으로 증가합니다. 이러한 알고리즘은 매우 비효율적이기 때문에 잘 사용하지 않습니다. O(2^n)의 복잡도를 가지는 대표적인 경우는 three-coloring problem입니다.
O(log n)	로그	입력의 크기가 기하급수적으로 증가하는 동안 실행시간은 선형적으로 증가합니다. 예를 들어 1000개의 요소를 처리하는 데 1초가 걸린다면 10000개를 처리하는데 2초, 100000개를 처리하는 데 3초가 걸리는 식입니다. O(log n)의 복잡도를 가지는 경우는 이진검색(Binary search)입니다.

Dominance Ranking

O( $n!$ ) >> O( $c^n$ ) >> O( $n^3$ ) >> O( $n^2$ ) >> O( $n \log n$ ) >> O( $n$ ) >> O( $\sqrt{n}$ ) >> O( $(\log n)^2$ ) >> O( $\log n$ ) >> O( $\frac{\log n}{\log \log n}$ ) >> O( $\log \log n$ ) >> O( $1$ )