1. BFS(Breadth First Search) : 너비우선 탐색
시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리
떨어져 있는 정점을 나중에 방문하는 순회 방법입니다.
너비우선 탐색을 위해서는 가까운 거리에 있는 정점들을 차례로 저장하고, 들어간 순서대로 꺼낼 수 있는 자료구조가 필요한데 , 이때 큐(queue)가 사용된다.
정점들이 방문될 때마다 큐에 인접 정점을 삽입하고, 더 이상 방문할 인접 정점이 없는 경우 큐의 맨 앞에서 정점을 꺼내 그 정점과 인접한 정점들을 차례대로 방문한다.
초기 상태의 큐에는 시작 정점만이 저장되어 있고, 너비우선 탐색 과정은 큐가 공백 상태가 될 때까지 계속된다.
2. 너비우선 탐색을 이용한 정점 방문 과정
BFS의 방문과정을 알아보겠습니다.
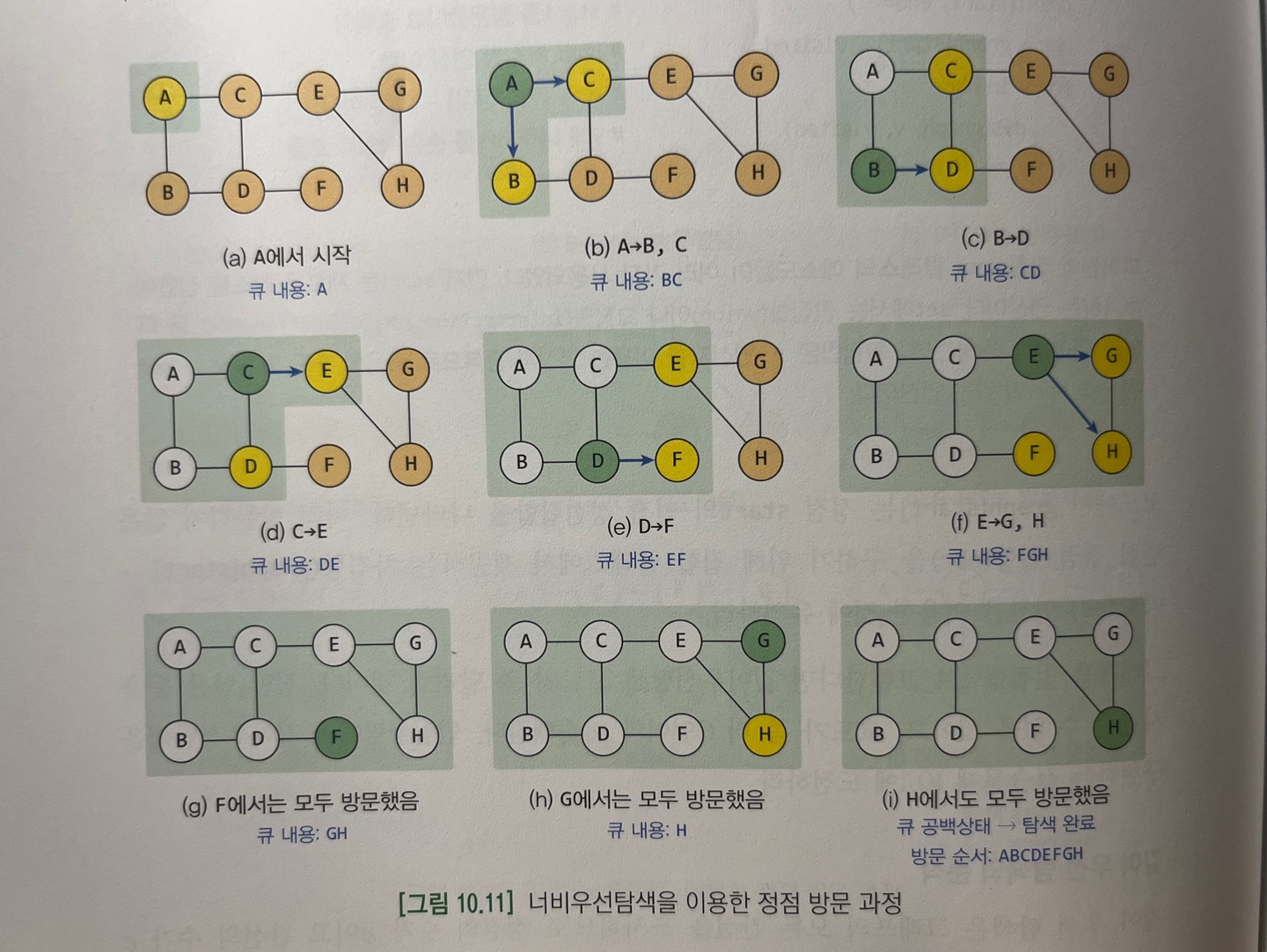
- 처음에는 큐에 A만 들어있다.
큐에서 A를 꺼내 인접 정점을 순서대로 방문한다. - 이제 큐에는 [B,C] 가 들어있다. 다시 큐에서 B를 꺼내고 B에서 갈 수 있는 인접 정점을 방문하고 큐에 삽입한다.
- 이제 큐에는 [C,D] 가 들어있다. 이 과정을 큐가 공백 상태가 될 때 까지 진행한다.
- (f) 상태에서 다음으로 F가 큐에서 꺼내지는데, 이미 모두 방문했으므로 더 이상 큐에 삽입할 정점이 없다.
이와 같이 큐의 모든 요소들이 처리되어 큐가 공백 상태이면 탐색은 종료된다.
문제를 풀면서 알아보겠습니다!
📝 BFS 예제
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
public class BFS_STUDY {
// 노드, 엣지, 시작점
static int N,E,S;
static int[][] Graph;
static boolean[] Visited;
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(bf.readLine());
N = Integer.parseInt(st.nextToken());
E = Integer.parseInt(st.nextToken());
S = Integer.parseInt(st.nextToken());
// 그래프와 방문 배열 초기화
// 0번 인덱스를 비워놓는 이유는 주로 노드 번호가 1부터 시작할 경우, 배열의 인덱스와 노드 번호를 일치시키기 위해서
Graph = new int[N+1][N+1];
Visited = new boolean[N+1];
for(int i=0; i<E; i++) {
st = new StringTokenizer(bf.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
// 양방향 엣지를 표현
Graph[u][v] = Graph[v][u] = 1;
}
// 함수 호출
BFS(Graph,Visited,S);
}
static void BFS(int[][] Graph,boolean[] Visited,int S) {
// BFS는 큐(선입선출)로 구현할 수 있다.
Queue<Integer> queue = new LinkedList<>();
StringBuilder sb = new StringBuilder();
// 시작점을 큐에 저장
queue.add(S);
// 시작점의 Visited 배열을 true로 저장
Visited[S] = true;
// 큐에 남은게 없을 때 까지
while (!queue.isEmpty()) {
// currentNum 에 큐에서 빼낸 수를 저장
int currentNum = queue.poll();
// 꺼낸 수 저장
sb.append(currentNum).append(" ");
// Graph[currentNum]의 길이(행)
for(int i=1; i<Graph[currentNum].length; i++) {
// 0이라면 , 즉 이어져 있지 않는 그래프라면 패스
if(Graph[currentNum][i] == 0) {
continue;
}
// 그래프가 이어져있다면
int next = i;
// 아직 방문하지 않은 노드의 Visited 배열을 true로
if(!Visited[next]) {
Visited[next] = true;
// 큐에 저장
queue.add(next);
}
}
}
// 최종 출력
System.out.println(sb);
}
}< 입력 >
4 5 1
1 2
1 3
1 4
2 4
3 4
< 출력 >
1 2 3 4
큐를 사용하여 문제를 풀었고, 2차원 배열을 만들어서 문제에 접근했는데 처음에 큐를 응용하여 푸는게 잘 이해가 가지 않아서,
BFS설명 YouTube
을 참고하여 문제를 풀어보았습니다.
2차원 배열에 연결되어 있는 그래프를 만들고, 그래프가 연결되어 있고,
(즉, Graph[u][v] = Graph[v][u] = 1 ) 아직 방문한적이 없는 노드라면 해당 노드를 방문해 Visited 배열을 true로 만들어주고, 해당 노드에 들어있는 원소들을 다 큐에 넣어줍니다.
재귀호출을 하는 DFS와 다르게, while (!queue.isEmpty()) { ... } 를 사용하여 큐에 남은 것이 없을 때까지 방문하는 것이 특징입니다.
📝 풀어보면 좋을 문제
📎 백준 1260번 - DFS와 BFS
DFS코드 부분은 편의상 삭제했습니다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class Baek_1260{
static int N,E,S;
static boolean[] Visited;
static ArrayList<Integer>A[];
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(bf.readLine());
N = Integer.parseInt(st.nextToken());
E = Integer.parseInt(st.nextToken());
S = Integer.parseInt(st.nextToken());
A = new ArrayList[N+1];
for(int i=1; i<=N; i++) {
A[i] = new ArrayList<Integer>();
}
for(int i=0; i<E; i++) {
st = new StringTokenizer(bf.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
// 양방향 엣지 그래프 표현
A[u].add(v);
A[v].add(u);
}
// 오름차순 정렬
// 가장 작은 수 부터 방문할 수 있음
for(int i=1; i<=N; i++) {
Collections.sort(A[i]);
}
Visited = new boolean[N+1];
BFS(S);
System.out.println();
}
public static void BFS(int node) {
Queue<Integer> queue = new LinkedList<>();
Visited[node] = true;
queue.add(node);
while(!queue.isEmpty()) {
int k = queue.poll();
System.out.print(k + " ");
for(int i : A[k]) {
if(!Visited[i]) {
Visited[i] = true;
queue.add(i);
}
}
}
}
}
