1. 큐(Queue)

스택과 반대로 선입선출(First - In First Out : FIFO) 구조.

즉, 먼저 들어온것이 먼저 나갑니다.

가장 앞에 있는 사람, 즉 가장 먼저 온 사람이 가장 먼저 서비스를 받아야하고, 방금 도착한 사람은 줄의 맨 뒤에 서서 대기합니다.

rear(후단) : 큐에서 삽입이 일어나는 곳
front(전단) : 큐에서 삭제가 일어나는 곳

큐는 스택과 마찬가지로 2가지 방법으로 구현이 가능 합니다.

1. 배열
2. 연결리스트

• 배열
  배열을 이용하여 큐를 만드는 경우 원형 큐 형태로 구현.
  원형 큐 형태를 구현함으로서 배열의 첫 인덱스가 0 이 아닐 수 있습니다.
  이를 통해 배열의 마지막 인덱스에 데이터가 있어도 앞서 들어온 데이터를 꺼내 앞쪽 인덱스의 배열은 비어있는 경우 앞 인덱스의 요소들에도 데이터를 넣을 수 있어 FIFO 구현이 간단해집니다.

Queue ADT

• Queue() : 비어 있는 새로운 큐를 만든다.
• enqueue(x) : 항목 x를 큐의 맨 뒤에 추가한다. -> 시간 복잡도 O(1)
• dequeue() : 큐의 맨 앞에 있는 항목을 꺼내 반환한다.
  -> 시간 복잡도 O(n)
• peek() : 큐의 맨 앞에 있는 항목을 꺼내 반환한다.
• isEmpty() : 큐가 비어있는지 확인하고 비어있으면 true 를 아니면 false 를 반환한다.
• isFull() : 큐가 꽉 차있는지 확인
• size() : 큐의 모든 항목들의 개수를 반환한다.
• add() : 큐에 값 추가 / 삽입성공하면 true 반환 ,없으면 오류발생
• offer() : 큐에 값 추가
• poll() : 큐에 값 제거

✅ offer() vs add()

Queue 인터페이스에서 offer()와 add()는 요소를 큐에 추가하는 메서드입니다. 하지만 두 메서드 사이에는 몇 가지 중요한 차이점이 있습니다.

1. 반환 값과 예외 처리

add() : 성공적으로 요소를 추가하면 true를 반환하고, 큐에 더 이상 공간이 없어 요소를 추가할 수 없는 경우 IllegalStateException을 던집니다.
offer(): 성공적으로 요소를 추가하면 true를 반환하고, 큐에 더 이상 공간이 없어 요소를 추가할 수 없는 경우 false를 반환합니다.

2. 사용하는 큐의 종류

위의 차이점 때문에, 고정 크기의 큐 (예: ArrayBlockingQueue) 에서는 offer()를 사용하는 것이 더 안전할 수 있습니다. 이는 큐가 꽉 찼을 때 예외를 던지지 않기 때문입니다.
반면, 무한한 크기의 큐 (예: LinkedList) 에서는 add()와 offer() 사이에 실질적인 차이가 거의 없습니다.

3. 성능 차이

대부분의 Queue 구현에서, add()와 offer() 사이에는 성능 차이가 거의 없습니다. 주된 차이는 어떻게 실패 상황을 처리하는지에 있습니다.
결론적으로, 성능 차이보다는 어떻게 큐가 꽉 찼을 때의 실패 상황을 처리할 것인지에 따라 add() 또는 offer()를 선택하는 것이 중요합니다.

.

.

인큐 / 디큐 처리할 때 시간 복잡도

배열로 만든 일반 큐: 복잡도 O(n) -> pop() 연산에서
배열로 만든 원형 큐 : 복잡도 O(1)

2. 큐는 어디에 사용될까 ?

• 버퍼(buffer) - 컴퓨터에서 데이터를 주고받을 때 각 주변장치들 사이에 존재하는 속도의 차이나 시간차이를 극복하기 위한 임시 기억 장치로 큐가 사용
• 인쇄 작업 큐 : 프린터는 CPU에 비해 상대적으로 속도가 느립니다.
  따라서 CPU는 빠른 속도로 인쇄 데이터를 만들어 프린터의 인쇄 작업큐에 보낸 다음 다른 작업으로 넘어갑니다.
  프린터는 일정한 속도로 인쇄 작업 큐에서 순서대로 데이터를 가져와 인쇄합니다.

3. 큐(Queue) 의 종류

3-1. 선형 큐

선형 큐에는 어떤 문제가 있을까 ?

✅ 선형 큐의 단점

선형 큐에서 삽입 및 삭제를 반복하다 보면, rear가 맨 마지막 인덱스를 가리키고, 앞에는 비어 있을 수 있지만 이를 꽉 찼다고 인식합니다.

이는 실제 데이터는 삭제 때마다 한 칸 앞으로 이동시키지 않았고, 인덱스 단위로 큐의 연산을 진행했기 때문입니다.

그래서 생겨난 아이디어가 원형 큐 입니다. 코딩에서는 1차원 배열을 활용하지만 처음과 끝이 원형처럼 이어져 있다고 가정합니다.

3-2. 원형 큐 ( 실제로 리스트가 원형인것은 아니고 원형으로 생각하고 사용한다.)

✅ 기본적으로 리스트의 크기가 고정되어야 합니다.

rear : 큐에 가장 최근에 삽입된 항목의 위치를 저장
front : 가장 최근에 삭제된 항목의 위치를 저장
처음에는 rear == front == 0

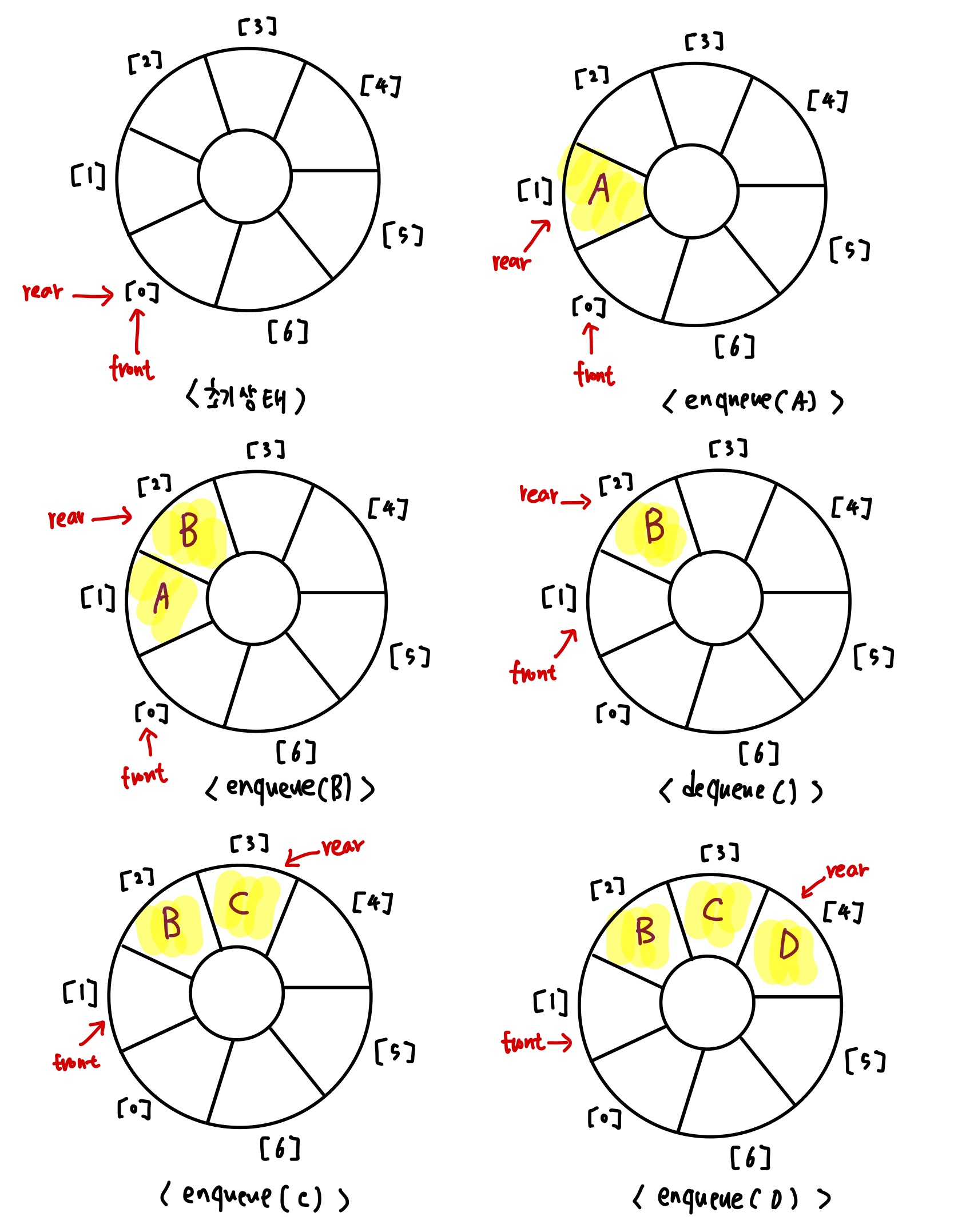
0부터 계속 증가하다가 MAX_QSIZE - 1 이 되면 다음은 MAX_QSIZE 가 아니라 다시 0 이 되는것입니다.

그렇다면 front와 rear를 어떻게 회전(이동) 시킬까 ?

front <- (front+1) % MAX_QSIZE / rear <- (rear+1) % MAX_QSIZE
삭제를 하더라도 선형큐와 같이 항목들을 앞으로 하나씩 당길 필요가 없습니다. 삽입도 마찬가지입니다. 인덱스만 변경됩니. 따라서 삽입,삭제 연산의 시간복잡도는 모두 O(1) 입니다.

4. 원형 큐(Queue)의 공백/포화/오류 상태

.
.

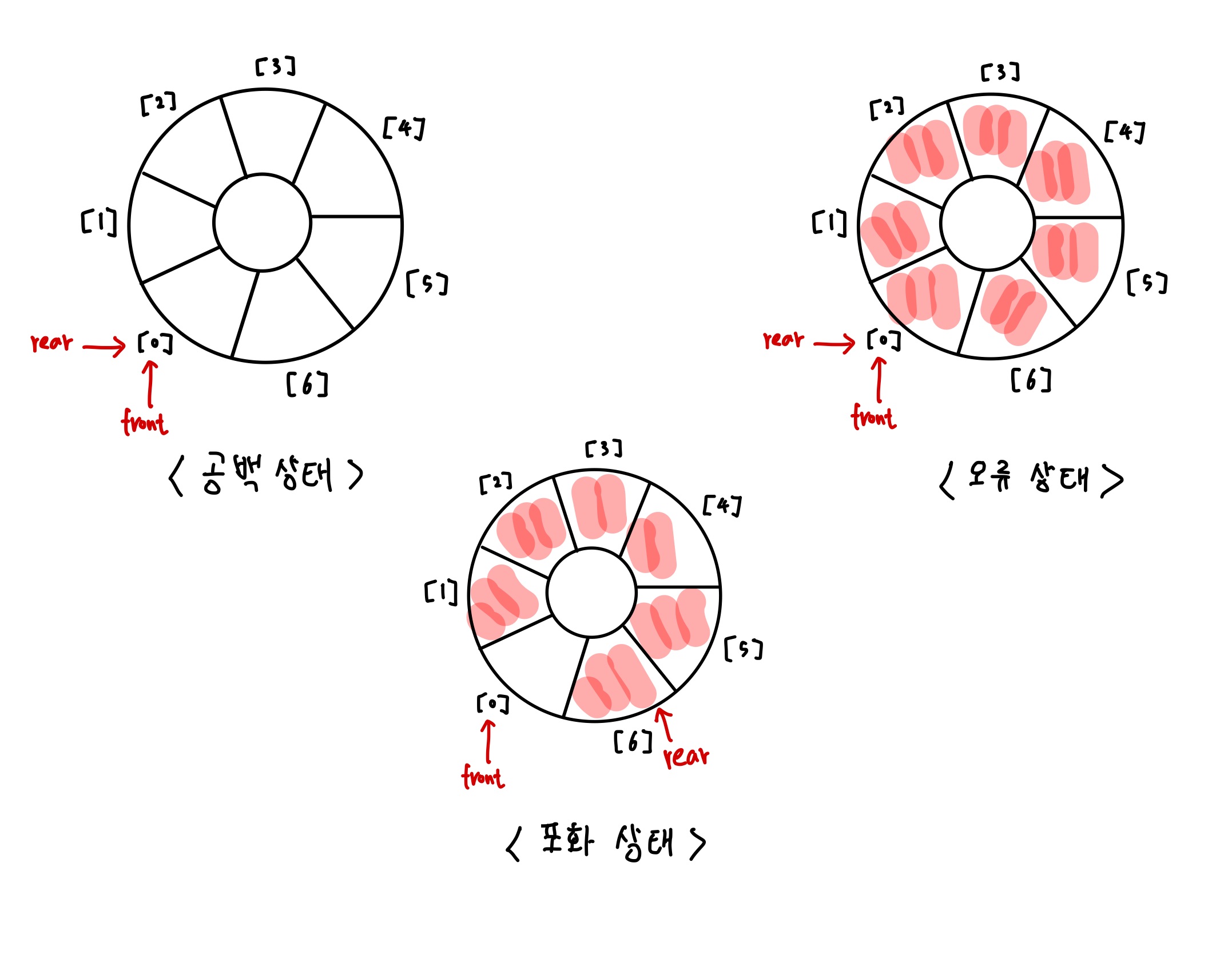
마지막으로 큐를 활용한 문제를 풀어보면서 정리해보겠습니다.

📝 문제

📎 백준 1158번 / 요세푸스문제

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;


public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(bf.readLine());
        int N = Integer.parseInt(st.nextToken());
        int K= Integer.parseInt(st.nextToken());
        Queue<Integer> queue = new LinkedList<>();
		// 1 ~ N 까지 숫자를 큐에 저장 
        for(int i=1; i<=N; i++) {
            queue.offer(i);
        }
      
        StringBuilder sb = new StringBuilder("<");
        // 큐의 크기가 1보다 클때
        while(queue.size() > 1 ) {
       		// 1부터 K번째 수 전까지 큐의 맨 앞 숫자를 삭제 -> 맨 뒤에 추가
            for(int i=1; i<K; i++) {          // 0 ~ K  
                queue.offer(queue.poll());
            }
            // K번째 수를 저장
            sb.append(queue.poll()).append(", ");
        }
        // while 문이 다 돌면 큐에는 원소 하나만 남아있을것이다.
        // 그렇다면 남은 원소를 다시 저장
        if(queue.size() == 1) {
            sb.append(queue.poll()).append(">");
        }
        System.out.println(sb);
    }
}

.
.

열공 ‼️