[HUFS/Algorithm] 재귀, 선택

2. Recursion 재귀 맛보기

1부터 n까지의 합을 계산해보자

루프를 활용한 방법🔽

재귀적으로 작성하는 법🔽

sum(n) = sum(n-1) + n 의 점화식이며, 바닥조건은 sum(1) = 1 이다.

따라서 코드는

def sum(n):
  if n==1: return 1
  return sum(n-1) + n

으로 나타낼 수 있다.

수행시간 역시 재귀적으로 정의한 다음 > Big O 를 계산하는 순서로 푼다.
T(n) = T(n-1) + 1 과 같이 정의할 수 있으며, T(1) = 1 이다.

이를 Big O 로 나타내는 방법은 '전개해보는 것' 이다. 전개하는 것이란 점화식을 게속해서 하나씩 푸는 것이다. n은 -1을 , 1 을 더해주는 식을 말이다!

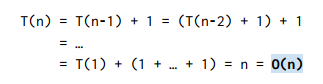
결국 O(n) 으로 표현할 수 있다.

재귀의 방법 두 번째.🔽
좀 다르게 계산하는 방법도 있다. sum(a,b) 로 인자를 두 개 받으며, 중간값을 m = (a+b) // 2 로 지정하는 것이다. 그리고 나서 호출 시 sum(a,m) + sum(m+1, b) 를 호출해준다. 바닥조건은? a와 b 사이에 아무런 숫자가 없을 때 = 즉 같은 숫자인지를 검사해주고 a 를 반환하면 된다.

코드는 다음과 같다.

def sum(a, b):
	if a == b:
		return a 
	m = (a+b)//2
	return sum(a, m) + sum(m+1, b)

재귀함수의 특징은 재귀함수와 바닥조건을 정의해주기만하면 나머지 조건이나 복잡한 연산의 과정은 코드에서 구현할 필요가 없다는 것이다. 다시말해, 적당한 식을 주면 나머지는 컴퓨터를 믿으면 된다!

수행시간 역시 재귀적으로 구성한다는 원칙에 따라
T(n) = T(n/2) + T(n/2) + c = 2T(n/2) + c, T(1) = 1 로 구성할 수 있다.
상수항 c 는 위 함수에서 재귀함수 호출 부분을 제외한 비교, 덧셈 나눗셈 등 기본 연산자를 퉁친 것이다.

역시나 Big O 연산을 위해선 위 T(n) 을 풀어헤쳐야 한다. 한 번 전개할 때 2를 곱하고, n/2 를 해주고, c 를 더해줘야 한다! 어렵지만 과정은 다음과 같다.

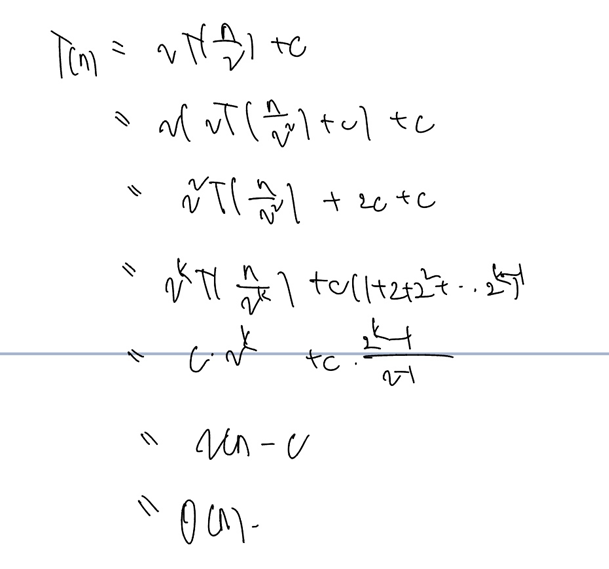
리스트의 값을 거꾸로 배치하기🔽
A를 반대방향으로 재배치하는 함수 reverse(A) 를 재귀적으로 작성해보자.

1)

def reverse(A):
	if len(A) == 1:
		return A
	return reverse(A[1:]) + A[0] 

그러나 A[1:] 의 연산이 이미 수행시간이 O(n) 이다. 그러면
T(n) = T(n-1) + cn = O(n^2) 이 되어버린다!

2) 양 끝을 오가며 바꿔주기.

def reverse(A, start, stop): 
	if start < stop-1: 
		A[start], A[stop-1] = A[stop-1], A[start]
	reverse(A, start+1, stop-1)

이번엔 매개변수가 리스트, 시작시점, 끝지점으로 3개이다. 시작지점이 끝지점 - 1 보다 작기만 하면, 서로를 바꾸고, 시작지점은 하나 증가시키고 끝지점은 하나 감소시켜 다시 호출하는 함수다.

이제 수행시간 점화식은 T(n) = T(n-2) + c , T(1) = c 가 된다. (양 끝에서 하나씩 총 두 개 줄었으므로)

3. Selection (선택문제)

🧩1. 가장 큰 수 찾기 (k = n)

일단 기본 수도 코드는 다음과 같다.

currentMax = A[0] 
for i = 1 to n-1 do
	if currentMax < A[i] 
		currentMax = A[i]
return currentMax

모든 수에 대한 비교가 이루어지므로 수행회수는 n-1 이다.

🤔 다른 방법으로 비교가 가능할까?
토너먼트 방식으로 비교가 가능하다. 이 경우에도 n-1 번의 비교가 필요하다.
🤔 n-1 보다 더 작아질 수 있을까?
하한 증명법으로 최소가 n-1 임을 증명할 수 있다.

🧩2. 가장 작은 수와 가장 큰 수를 모두 찾기

가장 작은 수를 n-1 번으로 찾고, 가장 작은 수를 제외하고 가장 큰 수를 n-2, 총 2n-3 으로 찾는 거 말고 다른 방법이 있나?

1. 토너먼트 식으로 n-1 비교로 작은 수를 먼저 찾는다. (이때 1라운드 탈락 한 수 중 큰 수가 존재한다.)

2. 탈락한 수는 n/2개 또는 n/2+1개

3. 따라서 큰 수 찾기 비교 횟수는 n/2-1 번

4. 전체 비교횟수는 3n/2 -2 번이면 충분하다.

이보다 적은 비교는 불가능!

🧩4. 임의의 k번째 작은 수 찾기

찾는 수가 존재할 범위를 줄여나감.

1. 전체 n개 중 k 번째 작은 수 존재.
2. 추가 작업으로 범위를 반으로 줄임 (n/2)
3. 추가작업으로 다시 반으로 줄임 (n/4)
4. 마지막 하나 남을 때까지 반복
5. 남는 하나가 찾는 값.

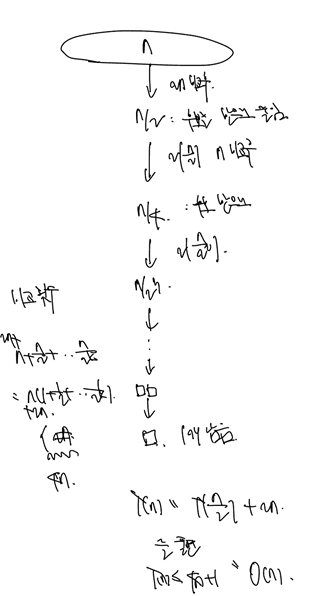
이 아이디어를 단순하게 구현한 알고리즘이 Quick Select 알고리즘이다.

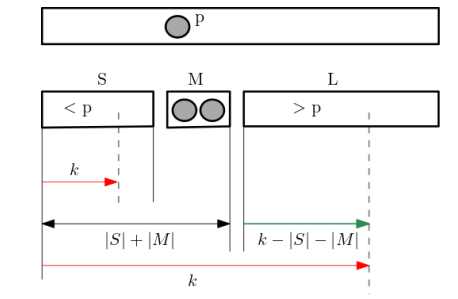
✅ Quick Select 알고리즘

1. 임의의 수 pivot = p 선택
2. p 와 비교하여 작으면 S, 같으면 M, 크면 L 로 분류
3. |S| > k(번째로 작은 수) 라면 S 안에 있음. 따라서 S 에서 K 번째로 작은 수가 답.
4. |S| + |M| < k 라면: L 에 있음.. L 에서 K 번째로 작은 수 찾기
5. 아니라면 M 에 있고, p를 리턴.