알고리즘 선택문제 소개
✅선택문제:
입력 : n개의 값과 k 값
출력 : k 번째로 작은 입력 값
목표 : 비교 횟수 최소화
✅ k = n 일 때, 최댓값을 찾는 문제임. (current < A[i] 비교, n-1번 비교로 항상 최댓값 찾기 가능, 이를 상한upperbound라 한다.)
만약 n-1번의 비교가 최소한 필요한 경우라면 이를 하한lowerbound라 한다.
- 현재는 upperbound와 lowerbound 가 일치하여 완전히 풀렸다!
이외에도 토너먼트방법으로 비교하여 최댓값을 찾는 방법도 있다. 그러나 이 경우에도 n-1 번의 비교가 최소한 필요하고, 무조건 찾기 가능하다.
✅ k = 1 일 때, 최솟값을 찾는 문제이므로 역시나 n-1번이 필요하다.
그러나 이 경우에 최대, 최소를 동시에 찾고싶다고 하자.
우선 n-1 번의 비교 연산으로 최대를 찾고, 최대를 뺀 후 n-2 번의 비교로 총 2n-3 번의 비교를 하는 방법이 있다. (upperbound)
이외에도 우선 최댓값을 찾는 연산을 n-1 번 수행한 후, 첫 라운드에서 탈락한 노드(n/2) 개만 가지고 최솟값을 찾는 비교 연산 n/2 -1 을 수행할 수 있다. 따라서 최종 비교는 3n/2 -2 가 된다. (lowerbound)
✅ k =1,2 : 제일 작은 값과 두 번째로 작은 값 찾기
n-1 + n-2 = 2n -3 번 비교 (upperbound)
역시나 토너먼트 방식을 이용하여 n-1 가장 작은 수를 고를 수 있다. 두번째로 작은 값은 무조건 첫번째로 작은 값에게 진다. 가장 작은 값에게 진 수는 round수개 일 것이므로 이들 사이 비교를 수행한다(round-1번 비교). round수-1 번을 하면 두 번째로 작은 최솟값도 찾을 수 있다. (8개 > 3라운드, 9개-16개 > 4라운드 ... -1)
따라서 이때에는 [logn] -1 올림이 필요하다. 총 n - [logn] - 2 의 총 비교연산이 필요하다!
알고리즘 선택(selection) 문제
n개의 값 중에서 k 번째로 작은 수 찾기
✅ Quick Select
n개의 수가 L이라는 리스트에 들어있다고 가정하자.
- p를 고른다. (random or L[0] or L[-1])
- p 보다 작은 값 A, 큰 값 B, 같은 값 M에 집어넣는다.
- if |A| > k : A에서 k 번째로 작은 값을 찾는다.(재귀적으로 찾는다, A를 L로 보는 것!) / elif |A| + |M| < k: B에서 k - |A|-|M| 번째 작은 수를 찾는다. / else: return p
코드는 다음과 같다.
def quick_select(L, K):
p = L[0]
A,B,M = [], [], []
for x in L:
if p > x : A.append(x)
elif p < x : B.append(x)
else: M.append(x)
if len(A) > k: return quick_select(A, k)
elif len(A) + len(M) < k: return quick_select(B, k-A-B)
else: return p 워스트케이스 T(n) = T(n-1) + n, T(1) = 1 이다. 이를 전개하면 n(n+1)/2 이며 O(n^2) 이다.
베스트케이스 T(n) = T(n/2) + n, T(1) = 1 이므로 T(n) <= 2n 이다. O(n) 이다.
평균적으로는 O(n) 이라 (이 부분은 어려우니 넘어가자) 성능이 좋다.
✅ MoM 알고리즘
MoM(L, K):
1. 전체 L 중 5개씩 그룹을 만든다. (n/5개의 그룹)
2. 각 그룹의 중간값을 구한다. (5개이므로 6번 비교하면 된다.) n/5 6 번의 비교
3. n/5개의 중간값들 중 또다시 중간값을 구한다. m = Mom(medians, |medians|/2) 이때는 T(n/5)번 비교이다.
4. 중간값의 중간값 = m(= m-star) 가 pivot 이 되어 m 보다 작은 값A, 큰 값B을 판단한다. (n번 비교)
5. A,B에 있으면 재귀호출, 아니면 return m* 한다. T(|A|) or T(|B|) <= T(n/c) 이다.
T(n) = 6n/5 + T(n/5) + n + T(n/c) = T(n/c) + T(n/5) + 11n/5
🤔 이때 c 는 얼마일까?
현재 X < m, W > m , Y or X > m < m
|X| >= n/4
|W| >= n/4
n/4 <= |A| <= 3n/4 , n/4 <= |B| <= 3n/4 따라서 c = 4/3 이다.
따라서 T(n) = T(3n/4) + T(n/5) + 11n/5 이다. (점화식)
T(n) = T(3n/4) + T(n/5) + 11n/5, T(1) = 1 풀기

귀납법을 통한 증명이다.
44n의 guess는 어떻게할까?
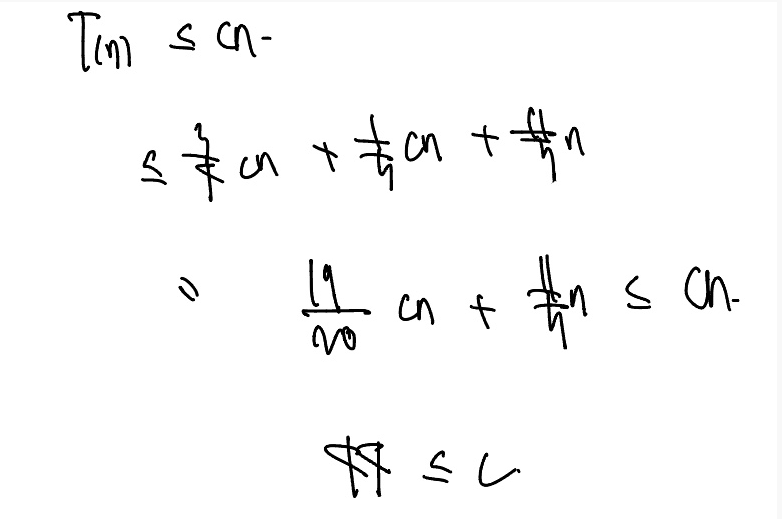
✅ Median of medians