[Interest] Learning to learn by gradient descent by gradient descent

[Learning to learn by gradient descent by gradient descent] 논문 리뷰

• 논문링크
  해당 논문은 Meta-learning 의 초기 형태를 다루고 있으며, 예전부터 내가 해오던 생각을 실제로 확인해준 논문이기도 하다. Meta-learning 의 개념을 몰랐을 때에도, 막연하게 미래에 내가 어떤 연구를 하면 좋을 지 생각하다가 '여러 task'에 적용가능한, '하나의 learning 방법을 지정해주면 스스로 학습하는' 완벽에 가까운 모델을 만들고 싶다는 상상을 한 적이 있었다. 논문을 읽으며 실제로 메타러닝이 두 가지 장점/특징이 있다는 걸 확인하고 매우 놀랐으며, 앞으로 몇가지 논문을 더 읽어볼 거다. 이 논문은 그 시작이 된다!

0. Abstract

이 논문에선 hand-designed optimization algorithms 이 아닌 optimization algorithm cast as a learning problem 문제를 푸는 방법을 제안한다. 학습 알고리즘 자체를 학습 가능하게 함으로써, 모델이 스스로 풀고자 하는 문제를 푸는 것이다! LSTM에 적용된 해당 방법은 당시 기준 더 나은 성능 & 다양한 태스크에서 동작함을 확인했다.

1. Introduction

machine learning 은 사실 다른말로 objective function f($\theta$) 가 주어지면 이에 맞게 optimizing 하는 과정으로 요약이 가능하다. 그리고, 여러 세타값을 조정해 loss function 함수값이 최소가 되는 세타값을 찾으면 된다. 이때 얼만큼 움직이는지는 미분을 하여 결정하며, 결과적으로 vanilla gradient descent 는 다음과 같다.

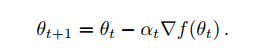
그러나 이 경우

• 업데이트에 미분 정보만 이용한다는 점
• second-order information 을 무시한다는 점 (1번 미분하므로)
  의 문제가 있었다. 이를 해결하기 위해 Hessian matrix (second order partial derivatives), Gauss-Newton matrix, Fisher information matrix 가 동원되었다.

딥러닝에 들어와서는, 고차원이며 & non-convex 문제를 풀기위한 optimization method 가 다양하게 등장했다. Nesterov, Rprop, Adagrad, RMSprop, ADAM 등이 그것이다. 이런식으로 optimizer을 정교하게 디자인하는 것은, 적어도 머신러닝에서는 '그' 문제를 잘 풀 순 있겠지만 다른 task에 대해선 잘 동작하지 못하는 결과를 나았고, combinatorial optimization 하에선 random strategy가 가장 좋다는 결과도 나왔다.

따라서 이 연구에서는 아예 다른 길을 제시하며, hand-designed update rules 에서 완전히 벗어나 learned rule = optimizer g를 사용할 것을 말하고 있다. 이때 optimizer g는 자신만의 파라미터를 가진다. 따라서 optimizee f를 업데이트하는데 필요한 룰은 다음과 같다.

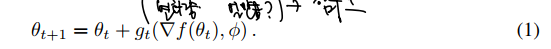
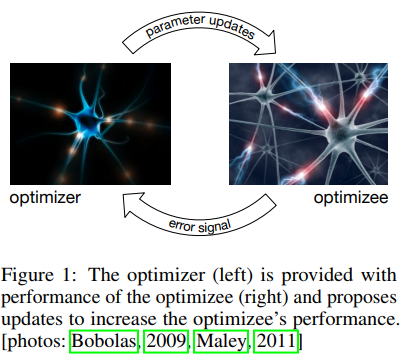
optimizee f에서 에러를 계산한다. (RNN) -> 이를 미분하고, 파라미터화 하여 g의 입력으로 한다 -> 따라서 g는 파라미터가 변할 수 있으며, g의 출력은 optimizee의 파라미터를 업데이트하는데 다시 사용된다.

• Optimizer는 따라서 자신만의 파라미터로 갖고, optimizee가 gradient를 전달해주면 이를 통해 theta 업데이트를 담당하는 역할을 한다.
• 따라서 optimizee 직접 미분을 통해 optimizer에게 이 값을 전달하는 역할을 하고, Optimizezr가 theta 업데이트를 해주면 최종 함수를 계산하는 역할을 한다.

1.1 Transfer learning and generalization

과거에는 풀고자 하는 문제에 대해 문제의 특징을 분석하고, 분석한 인사이트를 바탕으로 algorithm을 직접 작성했다면, 논문에서ㅢ 접근은 예시를 바탕으로 풀고자 하는 문제의 'class of problems' 를 정의하는 것이다.

또한 여기서의 generalization 이란 한 모델 내에서 봤던 데이터/못본 데이터에 대한 예측으로 확장이 아닌 transfer knowledge between different problems 임을 명시하고 있다. 이렇게 되면 generalization 의 하나로 transfer learning 도 제시할 수 있게된다.

1.2 A brief history and related work

• Lake et al. 2016이 AI에서의 learning to lean 중요성 제시
• Santoro et al. 2016 generalization 을 위한 multi-task learning 제시
• Schmidhuber 1992, 1993이 가중치를 변형할 수 있는 network 제시. 이후 gradient descent 가 아닌 search strategy 제시한 1997 논문이나, step-sizes 를 고르기 위한 controller 를 학습시키는 reinforcement learning (Daniel et al., 2016) 등장
• 최종적으로 이 논문은 Younger et al., Horchreiter et al., 2016의 backpropagation output 이 일반 network 뿐 아니라 additional learning network 까지 동시에 feed 된다는 아이디어의 논문에서 영감을 얻었다 밝힌다. 여기서 스케일을 넓혀, neural network 문제를 풀기위한 optimizer를 만든 것!

2. Learning to learn with recurrent neural networks

• 목표는 optimizer를 파라미터화하는 것이다
• 그렇다면 optimizer가 좋다는 것은 어떤 것일까? expected loss 식을 정의하면
  
• 최종 loss 는 결국 optimizee 에서 계산한다고 했다. 이것이 theta * 로 표시된 부분이며, optimizee는 또다시 optimizer 파라미터를 내부적으로 포함한다.

다시, 이를 f와 w를 도입하여 조금 더 정교화해보자. 실험에서는 RNN을 도입했으므로 RNN 구조와 각 t step 에서의 계산값의 expected loss 가 최종으로 계산해야 하는 값이다.

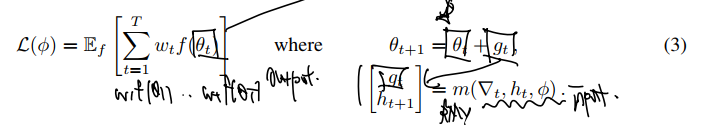
• RNN input으로 들어가는 건, 1) t시점에서의 Optimizee gradient 2) RNN hidden state 3) Optimizer paramters 이다.
• 중요하게 Optimier paramters 는 theta의 업데이트 규칙을 업데이트하기 위해 도입되었다 하였다. (과거에는 업데이트 규칙이라곤 lr X gradient였는데, 현재는 위의 3가지가 RNN 계산으로 들어갔으니 규칙이 매우 복잡해졌다.)
• 이로부터 theta 를 업데이트한다. 이 theta는 최종적으로 Optimizee의 파라미터이기도 하면서 f 함숫값을 만들기도 한다.
• 마지막으로 Loss fuction 을 계산해주면 되고, 여기서 나온 Loss 는 또다시 t시점에서의 Optimizee gradient 1) 로 들어가게 될 것이다.
  

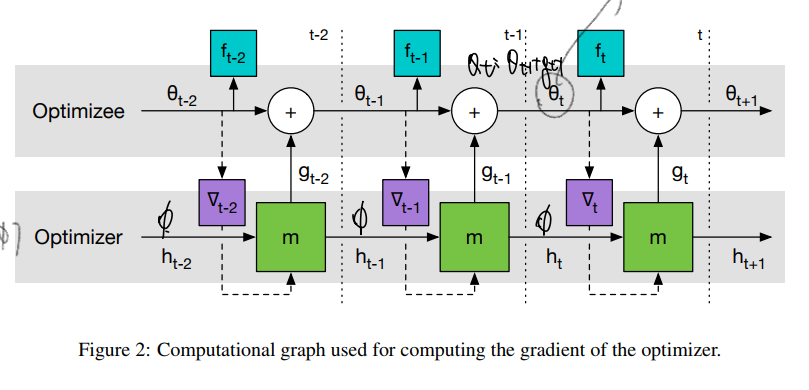
중요한 건 이렇게 Optimizer와 Optimizee 의 층위를 두게되면, optimizee의 gradient는 optimizer paramters 에게 더이상 의존하지 않아 second derivatives 가 필요가 없어진다. (이유는 t시점에서 optimizer paramters 는 t+1 시점의 Optimizee theta 에 영향을 주게되고, 따라서 같은 시점간 영향을 준 적이 없기에 다음 값이 0과 같기 때문이다.) 따라서 2차 미분의 문제가 사라진다.

2.1 Coordinatewise LSTM optimizer

• RNN 구조를 도입함에 있어 큰 문제는 최소한 tens of thousands of paramters 를 optimize 해야했기에 숫자가 너무 많다는 것이었다.
• 이 문제를 Optimizer M을 도입하면서 자연스레 해결할 수 있었다. 이를 논문에선 coordinatewise network 이라 함.
• 따라서 optimizer 자체는 single 로 두고, 이들의 파라미터를 여러 optimizee의 파라미터가 공유하는 형태가 된다.
• 각 coordinate 에 대한 다른 behavior는 각 objective function paramter 마다 분리된 activations 로 가능하게 하였다.
• 이때 optimizer로 LSTM이 사용되었으며, input으로 optimizee 의 gradient, previous hidden state을, output으로 같은 구성체의 optimizee를 업데이트하기 위한 값을 내놓는다.
• 사실 여기에서 input으로 들어오는 optimizee gradient 를 이용한다는 것이나, hidden state를 이용한다는 것 자체는 큰 차이가 없다. 중요한 것은, 모든 LSTM이 공유된 파라미터를 사용한다는 것!

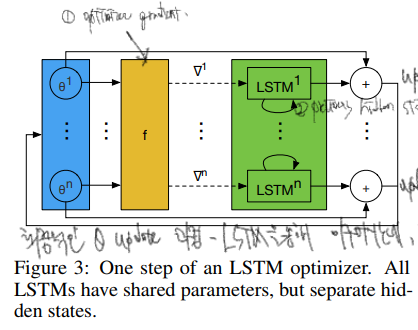
Preprocessing and postprocessing
LSTM Optimizer의 입력과 출력의 스케일을 맞춰주는 처리가 적용되어야 했다.

3. Experiments

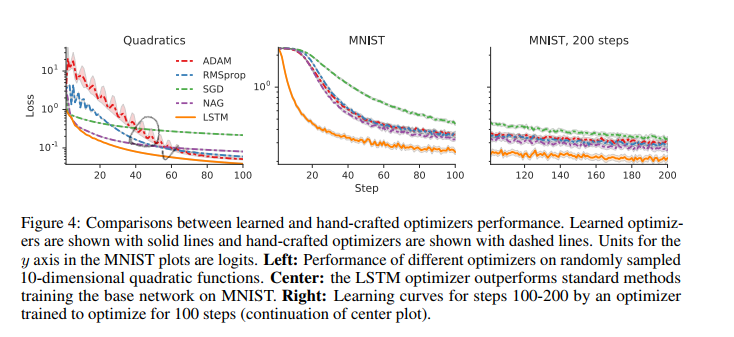
• hand crafted optimizer와의 비교.
• 가장 왼쪽은 10-dimensional quadratic function 에서 랜덤샘플된 서로다른 optimizers 들의 성능이다.
• MNIST 데이터에서 LSTM optimizer가 압도적인 모습.
• 100 step 이후에도 이러한 경향이 유지된다.

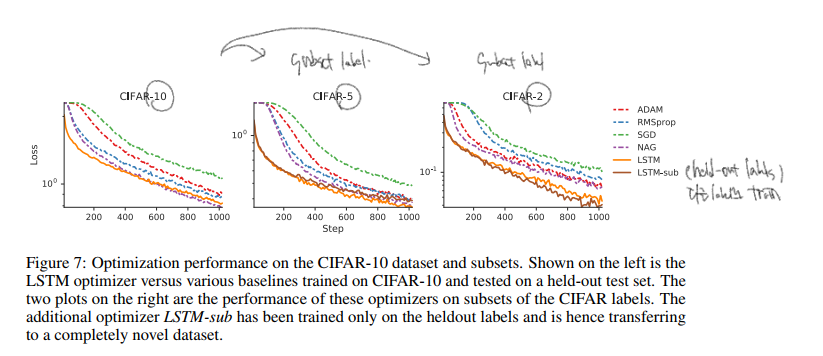
• CIFAR-10 에서의 성능이다.
• CIFAR-10에서 훈련되었으며 held-out test set 에서 비교했다.
• label 10, subset 5, subset 2에서 측정했다.
• LSTM-sub 라는 것은 오직 heldout labels 에서만 훈련되고, transferring to a completely novel dataset 이라 주장한다.

• Neural Art 에 관한 성능이다.
• 1) resolution 2) style image 가 같을 경우 LSTM 이 다른 optimizer 성능을 뛰어넘음을 확인할 수 있다.
• test time 에서 1) 2) 가 바뀌어도 잘 동작하는 것을 확인했다.
• Figure 을 보면, 왼쪽은 test 이미지에 training style, resolution 을 적용한 결과고, (중간사진이 결과다.) 오른쪽은 double the resolution 의 결과이다.

My Question

• Meta-Learning 을 NLP에 접목한 사례는 없을까?
• 결국 '학습에 대한 학습'인데, Optimizer을 RNN/LSTM 외에 다르게 적용시킨 형태는 없을까?
• Object function 을 다양하게만 주면 정말 다양한 학습에 이용되지 않을까?
• 그렇다면 한계는 무엇인가?