변분법과 오일러-라그랑지 방정식
오일러-라그랑지 방정식은 변분법의 기초가 되는 방정식으로서 역학에서 중요한 역할을 하고 있다고 한다. PRML 의 미분 엔트로피가 최대가 된다, 임을 증명하기 위해 라그랑주 승수, 변분법이 도입되었는데, 이때 변분법에 대해 알지 못했다. 이제 몇가지 자료들을 통해 정리한 변분법을 이해해보자!
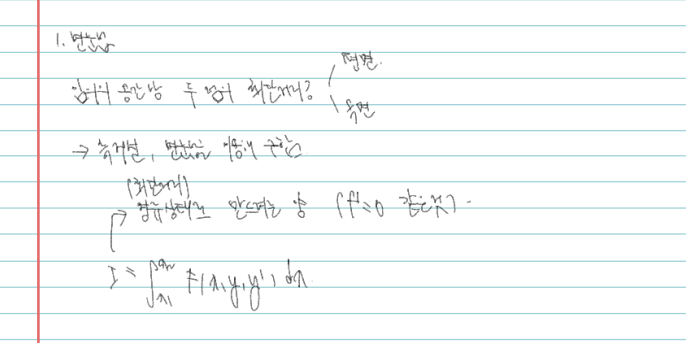
임의의 공간상에 있는 두 점의 거리를 구하려면 어떻게 해야할까? 두 점이 평면이라면 쉽게 식을 쓸 수 있고, 곡면이라도 식을 쓰는 것이 가능할 것이다. 어떤 공간이든 두 점의 최단거리를 측지선이라 하고 이 같은 문제를 변분법을 통해 풀 수 있다. 다시말해 변분법은 특히나 적분값에 있어서 최대나 최소를 구할 때 사용한다. 호의 길이는 아래와 같이 1+y'^2에 루트를 씌운 값을 적분하여 할 수 있다. (🤔여기서는 당연한 내용이므로 받아들이자!)
따라서 변분법으로 풀려는 문제는, 아래의 I를 minimize 하는 것이다.

다시 그림으로 이를 이해해보자. (x1, y1)과 (x2, y2)가 존재할 때 두 점을 잇는 실제 최소 거리의 곡선을 극치곡선 y(x), 우리가 구한 곡선은 변분곡선 Y(x)라 하자.
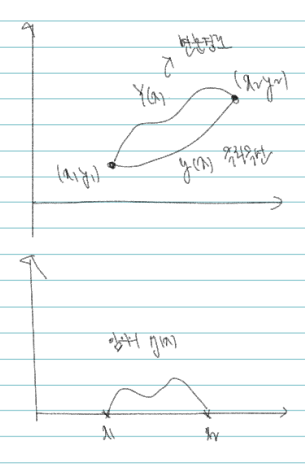
여기서 아래의 에타(x) 그림은 임의로 설정한 함수이며, 극치곡선에 더해져 변분곡선의 보정값 역할을 한다. 식으로 쓰면 다음과 같다.
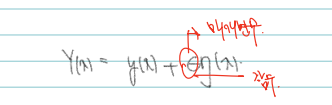
이제 아까 minimize 하기로 한 I를 다시보자. 여기서 y' 대신 우리는 Y' 을 써야한다! (y'은 정답이고, 우리가 해야하는 것은 함수 Y(x)에서 곡선의 거리를 최소화해야 하므로.)

식을 쓰고 에타에 대해 미분해둔 값을 써두었다. 왜 에타에 대해 미분하지? 보정값을 찾는 것이 목표인데 이때 임의의 함수 에타는 고정이며, 따라서 우리는 Y(x) = y(x)가 되는 지점을 찾기위해, 즉 에타 = 0 에서 dI/d에타 = 0 인 지점을 찾아야 한다. 마치 함수의 최솟값을 찾기위해 함수' = 0 이 되는 지점을 찾는 것과 같다! 여기선 I가 매개변수 에타를 변수로 하는 함수이므로, 다른 것이 아닌 에타에 대해 미분해주는 것이다.
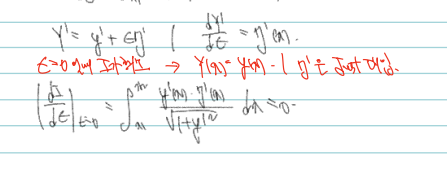
이제 처음 정의한 식을 미분해서 구한 값을 한 번 더 정리할 수 있다. 이때 우리는 에타 = 0 인 상황에서 dI/d에타 = 0 인 지점을 찾는 것이 목표이므로, 에타가 0임은 이미 가정하고 있다. 따라서 1) Y(x) = y(x) 라는 사실과 2) dY'/d에타 = 에타'(x) 임을 이용하면 위와 같이 정리가 가능하다.
이제 이 식을 부분적분법을 사용해서 풀 수 있다. 적분법에 대한 간단한 확인을 (https://ko.khanacademy.org/math/integral-calculus/ic-integration/ic-integration-by-parts/v/deriving-integration-by-parts-formula) 여기서 할 수 있다. 부분적분을 하기위해 u, v를 정의하고, 이를 아래의 식으로 푼다.

부분적분은 대입하면 끝이므로 추가적인 설명은 생략하고 가장 아래 식을 살펴보도록 하자. 우리가 구하려는 식의 값은 결국 0이다. 그런데 에타(x1) = 에타(x2) = 0이므로 첫항을 날리는 것이 가능하다. (이유는 처음 그린 그래프에 있다.) 두번째 항 역시 에타는 0이 되지 않으므로, 뒷부분이 0 이어야 하는데, 따라서 x에 대해 미분된 빨간 박스를 친 부분이 0이다.
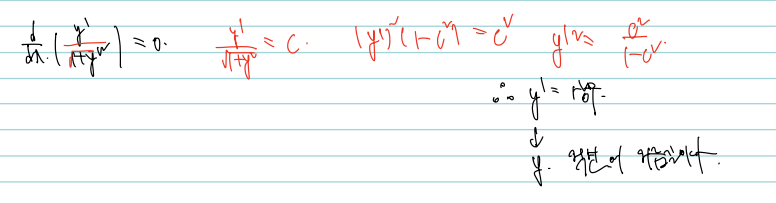
빨간박스만 가져왔다. 미분값이 0이므로 해당 값은 상수이고, 이를 y'에 대해서 풀면 y'은 결국 const라는 결론이 도출된다. 따라서 y은 상수 X 변수 형태인, 1차식 직선일 것이다. 이것으로 변분법을 통해 두 점을 잇는 가장 짧은 곡선은 직선임을 증명했다.
일반화 ➡️ 오일러-라그랑주 방정식
위를 일반화해보자. 아까 확인한 곡선의 길이 공식을 F(x, Y, Y') 으로 일반화된 함수로 뜯어고칠 것이다. 그래도 상황은 다르지 않다. Y(x)와 y(x) 가 있으면, y(x)가 극소(또는 극대)일 것이고, 에타 = 0 일 때 차이가 최소화되는 지점 dI/d에타 = 0 인 지점을 찾는 것이 목표이다.
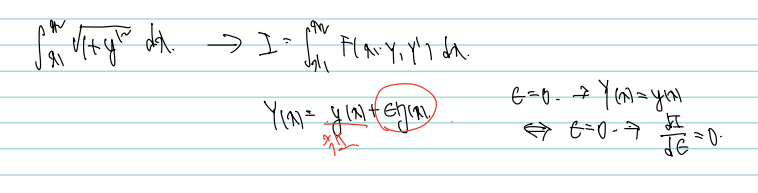
아까와 같이 dI/d에타를 해줄 것인데, 이번엔 I 식이 변했으므로 변한 I 식을 넣어주면 된다. 어렵진 않고 곡선의 길이 공식 대신, F를 에타에 대해 편미분한 그 값을 넣어주면된다!

여기서
- chain rule을 사용하여 2 line을
- 2 line 에서 에타 = 0 인 상황을 이용하여 3 line 으로,
- 3 line 에서 두 번째 항을 부분적분하여 4 line 으로 쓸 수 있고
4 line 에선 역시나 부분적분으로 표현된 첫 항은 날리고 이제 뒷 항에만 집중하면 된다.
두번째 항만 부분적분 했으므로 line 3의 첫항과 line 4의 날린 부분을 제외한 값을 적분으로 연결한다. 에타(x) 가 공통으로 포함되어 있으므로 묶을 수 있다.
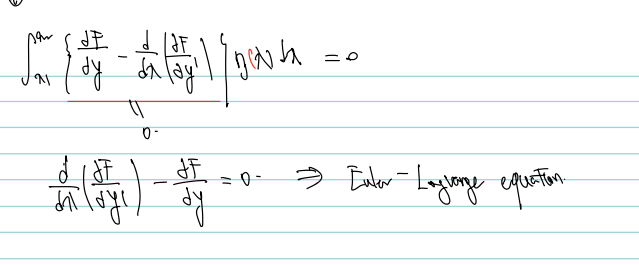
여기서 에타(x1) = 에타(x2) = 0 인 것이지 에타의 적분값은 0이 아님을 주의하자. 앞쪽에 곱해진 값이 0이 되어야하며, 이를 정리한 것이 Euler-Lagrange equation 이다!