[HUFS/Algorithm] Knapsack, Graph, DFS

박경민·2023년 6월 9일

[CS/Algorithm이론]

목록 보기

15/15

📚 목차

Knapsack
Knapsack1
Knapsack2
Graph
Graph traversal (DFS, preorder postorder)

Knapsack

Knapsack 은 Non-Polynomial 한 문제로 (왜? 가짓수만 해도 2^n이기 때문이다.) 어려운 문제에 속한다. 대표적인 다른 Non-Polynomial 로는 Subset이 있다.

Knapsack 의 문제 두 가지 유형을 생각해봤다.

0/1 Knapsack
fractional Knapsack (=Greey로 푸는 것이나 마찬가지, 귀류법으로 증명)

항상 답 자체는 2번 >= 1번이다. (잘라서 넣을 수 있으므로!)

🔨 Knapsack-1 : DP로 풀기(2차원)

DP의 정의를 다음과 같이 해보자. (용량은 K, 각 아이템의 크기는 S, 이익은 P 배열에 저장된다.)

DP[i][K] 를 아이템 1부터 i까지 중 아이템을 선택하여 용량 K인 가방에 넣을 수 있는 최대 이익이라 해보자. 그러면 구하는 것은 아이템 n개를 가지고 용량이 K인 가방에 넣을 때 최대 이익이므로 DP[n][K]가 된다. (어라? 이번에도 K가 이상하다. Psuedo Poly!)

아이템 i를 선택한 경우: 남은 무건 1부터 i-1까지 용량이 K-S[i] 인 배낭으로 최대 이익, 아이템 선택 이익 더함
아이템 i를 선택하지 않은 경우: 남은 물건 1부터 i-1까지 용량이 K인 배낭으로 최대 이익.

DP[i][K] = max(DP[i-1]K-S[i] + P[i], DP[i-1][K])

수행시간은 O(nK) 이지만 K는 입력의 크기가 아닌 입력으로 주어지는 수이므로 이것 역시 Pseudo Polynomial time 이다.

<DP 인덱스만 다르게 주고 같은 문제 풀기>
DP[i][p] 아이템 1-i로 가격 p를 맞췄을 때, 해당 가격을 맞추면서 선택한 아이템의 크기 합이 최소 값이라 정의. 크기 합이 정확히 K일 때를 봐야하므로 DP[n][] = K인 가장 높은 p를 찾으면 된다. (가방을 가장 덜 차지하는)

DP[i][p] = min(DP[i-1][p], DP[i-1]p-p[i]] + S[i])

i번째 아이템은 뽑지 않은 경우 나머지에서 크기를 보고, 뽑은 경우 i번째 크기를 더하고 남은 가격을 빼준 상태에서 크기를 본다. 둘 중 작은 것!

DP[n][P], DP[n][P-1] ... 중 첫 번째로 K이하가 될 때 이익이 정답이다. (아이템 n은 모두 탐색해봐야 하고, 그 중 가방 크기에 맞으면서(K) 이익이 최대가 될 경우를 구하므로)

🔨 Knapsack-2 : Backtracking으로 풀기

Tree 작성은 시험에 출제될 수 있으니 잘 알아두자.

가방 크기 K = 5
가격 P = [15, 16, 6]
크기 S = [3, 4, 2] 가 주어지면 가성비를 계산할 수 있다.
가성비 = [5, 4, 3]

Backtracking 으로 풀기위해선 기본적으로 준비해야 할 것이 또 있다. 가장 큰 예상 가격의 합을 갱신하는 MP 배열과, 해당 아이템을 담을지 0/1 결정하는 X 배열.

계산은 현재까지의 가격 합 P와 크기 합 S를 가지고 해나가면 된다.

이제 아이템 15, 16, 6짜리를 어떻게 담을지 결정하면 되는데 이때는 판단을 먼저 해야한다. 판단 조건으로는 2가지를 고려한다.

Size 조건: 더해도 사이즈를 넘지 않는지. 안넘으면 2번으로.
예상이익 조건: 해당 아이템을 넣었을 때(또는 넣지 않았을 때) 나머지 것들 포함하여 얻을 수 있는 최대 이익. fractional 로 계산. 예상이익이 MP(실제 가방에 담긴 가격) 보다 크면 넣는다.

이제 첫 아이템 X[1] = 1 을 고려해보자. (가격 15에, 크기 3)

사이즈 조건을 만족하므로 15를 넣는다고 가정하고
남은 크기 2의 자리는 fractional 로 채워본다. 다음 아이템을 반띵하여 8반큼 더 챙길 수 있으므로 15 + 23 > MP = 0 이므로 가방에 15를 넣는다.
MP는 실제 넣은 것만 계산하므로 현재까지 [0, 15]

따라서 P = 15, S = 3인 가방이 완성되었다. 다음 아이템 x[2] = 1을 고려해보자. 가격 16, 크기 4짜리 아이템이다.

사이즈 조건 만족 X. 끝.

이렇게 되면 더이상 내려가지 않고 x[2] = 0 담지 않는 길을 고려한다. 이럴 경우

사이즈 조건은 현재 3이므로 만족
예상이익은 15 + 6 (두번째 아이템은 fractional 에서 제외) > MP (15)이므로 가능.

따라서 현재까지 x = [1, 0] 이며, P = 15, S = 3이다.

x[3] = 1을 고려해보자. 세번째 아이템은 가격 6, 크기 2짜리이다.

사이즈 딱 5이므로 괜찮다
예상이익 15 + 6이다. > MP 이므로 넣는다.
P = 21, S = 5이며 MP = [0, 15, 21] 로 업데이트 한다.

다시 올라가 이번엔 x[3] = 0을 고려한다.

사이즈는 3이므로 괜찮으나
예상이익 15이다 MP 21보다 작으므로 안내려감

계속 올라가 이번엔 x[1] = 0을 고려했으나

사이즈 0이므로 괜찮으나
예상이익 0 + 16 + 3 < MP 이다. 따라서 내려가지 않음. 끝!

말로 하니 어려우나 사실 직접 해보면 더 쉽다. 직접 해보자!

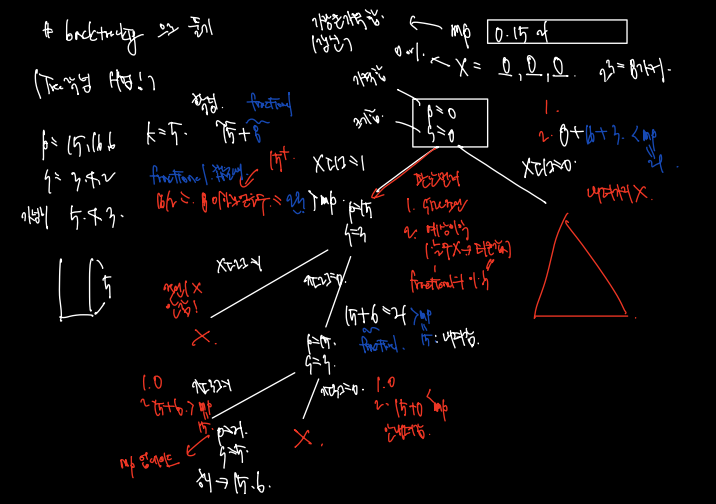
중요한 조건 2를 다시 보자.
조건 2는 그 길로 내려갔을 때 얻을 수 있는 최대 이익 VS 현재까지 best 이익을 비교하는 것이고, 최대 이익이 현재까지 이익보다도 작다면 내려가지 않는 것이다.

따라서 바로 위의 그림을 보면 알겠지만 단 4개의 노드 (만들어질 수 있는 15개 중) 만 만들고 해를 찾았다. 효율!

코드를 보자.

p(v)는 현재까지 이익의 합이고, s(v)는 현재까지 소비한 크기의 합이다.
코드는 크게 x[i] = 1 선택하는 경우와 x[i] = 0 선택하지 않는 경우로 나뉜다. 선택하지 않는 경우는 그래서 크기 검사가 없다. (size는 계속해서 빼고 있으므로 남은 size 라 생각하자.)
1. 사이즈 조건 완료. 2. 예상이익 조건의 경우 포함하는 경우는 현재까지 이익 + 그 물건의 이익 P[i] + 남은 예상이익 B이다. (포함이므로 크기에서 -S[i])
포함하지 않는 경우는 현재까지 이익 + 남은 예상이익 (포함 X이므로 크기 유지)
MP의 업데이트는 실제 포함할 경우에만 이루어진다. (MP자체가 실제 담은 가격만 기록하므로), 포함 여부에 따라 knapsack(i+1, size) 의 size 를 다르게 호출.

Graph algorithm

그래프 알고리즘의 기본 사항들을 알아보자.

방향(directed) 그래프 / 무방향(undirected) 그래프
Degree : In-degree (들어오는) / Out-Degree (나가는)
인접성
경로
사이클: 시작 = 끝인 경로
트리: 사이클이 없는 그래프
부그래프: 그래프의 일부분
연결성: 연결이란? 노드를 연결하는 경로가 존재하면 연결 있음

표현 방법은

인접행렬(2차원 리스트) => 엣지가 있다면 (노드1, 노드2) = 1, 없다면 =0으로 표현, 따라서 노드 수가 n이라면 n^2 메모리 필요.
다음 예시의 경우

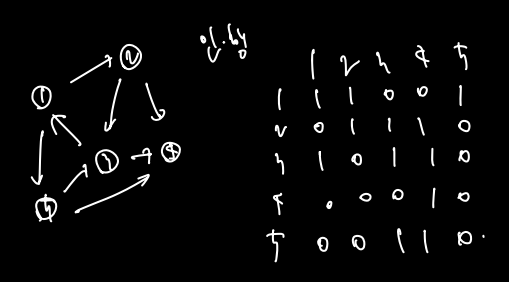
인접리스트 => 있는 것만 리스트에 담아 표현.
위의 예시의 경우

인접행렬과 인접 리스트의 시간 복잡도를 비교해보자.
1. (u,v) 연결 존재?
인접 행렬의 경우 O(1), 인접리스트의 u의 모든 degree를 조사해야 하므로 O(deg(u))
2. u에 인접한 모든 노드?
모든 노드를 알기 위해선 인접 행렬의 경우 행에 접근한다음 그 줄을 다 읽는다. O(n). 인접리스트의 경우 degree 수만큼 스캔하므로 O(deg(u))
3. u,v 삽입?
인접행렬의 경우 해당 칸에 쓰는 연산 O(1). 인접리스트 또한 append 한 번. O(1)
4. 기존 u,v 삭제?
인접행렬의 경우 [u][v] = 0 으로 O(1). 인접리스트의 경우 삭제하면 리스트 나머지 degree 들이 한 칸씩 앞으로 와야하므로 O(deg(u))
5. 메모리?
인접행렬의 경우 O(n^2). 인접 리스트의 경우 O(n + m). 이때 n은 노드 수, m은 엣지 수. 결국 기록하는 [1, 4] 와 같은 것들이 엣지이기 때문. 엣지 수는 방향 그래프일 경우 최대 n(n-1), 무방향일 경우 n(n-1)/2

트리의 경우 노드가 n이면 엣지는 n-1. 인접 행렬로 표현하면 O(n^2)이고 인접 리스트로 표현하면 O(n + n-1) = O(n) 이다!

그래프순회 (traversal)

그래프 순회의 경우 주어진 그래프가 있을 때 inorder, preorder, postorder 의 각 경우를 보는 것이다.

방법으로는 DFS(Depth First Search) 와 BFS(Beadth First Search) 가 있다. DFS 의 경우 preorder 와 같다. BFS는 0층을 다 돌고, 1층을 돌고, 2층을 도는 순서이다.

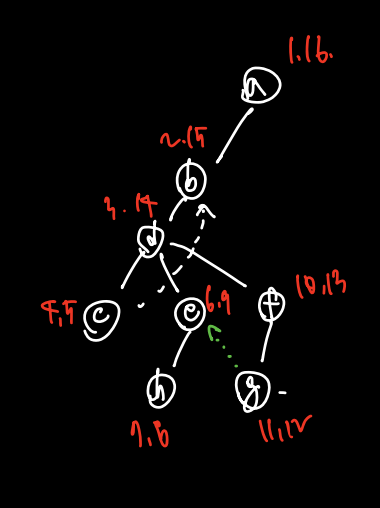
다음과 같은 그래프를 DFS 로 순회하면서 각각 preorder 와 post order 을 기록해볼 수 있다. 기본적으로 경로가 있는 방향으로 진행하면서 preorder 의 숫자를 늘려가며 기록하면 되는데, 갈 길이 방문했던 곳밖에 없는 경우 해당 위치에 post 를 기록해주면 된다.

DFS order 로 기록한 위 그래프의 순회는 a b d c e h f g 이다. (pre 만 쓰면 된다.)

이 방문순서를 위 그래프에 다시 표기한 후 트리를 그려볼 수 있다. (그래프 > 트리 전환의 순간)

트리에서 발견할 수 있는 edge 에는 4가지가 있다. 하나씩 알아보자.
0. Tree edge: 트리와 그래프 모두에서 나타나는 엣지를 말하며, 위 그래프에서 빨간색으로 표시한 부분을 말한다. (a,b) (b,d) (d,c) (d,e) (d,f), (e,h), (f,h) 7개

이제 주목해야 할 건 이를 제외한 나머지 엣지들이다. 그래프에만 있고 트리에는 없는 엣지들!