[HUFS/Algorithm] Subset sum, Sudoku, Knapsack

🔨 Subset sum

입력 A = {8, 6, 7, 5, 3, 10, 9} 가 주어지고, S = 15 합이 주어질 때, A의 Subset 중 합이 S가 되는 부분집합이 존재하면 True, 존재하지 않으면 False 를 리턴하는 문제. (Decision Problem 문제)

쉽게 생각할 수 있는 복잡도는 총 Subset 경우의 수 X sum 하는 시간인 O(2^n X n) 이나, 이런건 trivial algorithm 이라 한다.

이를 코드로 구현해보자.

Subset(A, i, S): 
	if S == 0: return True
    elif S < 0 or i < 0: return False # S가 너무 많이 빼졌거나 다 돌았는데도 S ==0이 나오지 않은 경우 (i는 카운트 같은 역할을 한다.)
    else: # z = A[i] 
        with = Subset(A, i-1, S-A[i]) # 포함을 가정한 경우, A에선 원소 z를 뺴고, 합에선 수 z를 뺀다. 
        without = Subset(A, i-1, S) # 포함하지 않음을 가정한 경우, A에서 원소 z가 빠졌지만, 합에서 수 z를 빼지 않았다. 
        return with or without # 둘 중 하나만 참이면 참을 반환한다. 둘 다 거짓이라는 것은 z를 포함하든, 포함하지 않든 S==0 을 만들 수 없다는 뜻으로 합의 조합이 없음을 의미한다. 

아이디어는 z를 계속 S에서 빼가며 S ==0 이면 합이 S인 Subset 이 존재하다고 믿는 것이다. 만약 빼는 도중 너무 많이 빼서 S <0 인 경우가 나오거나 다 뺏는데도 S > 0인 경우 (i <0) 조합이 없음을 의미하므로 False 를 반환한다.

시간복잡도는 with, without 을 호출할 때 각각 T(n) 인 문제가 T(n-1) 이 되므로 T(n) = 2T(n-1) + c = O(2^n) 이 된다. 위에서 trivial algorithm 으로 풀었을 때에서 합의 시간 정도를 제외한 부분집합을 구하기만 하는 정도의 시간이다!

부분집합을 출력하기 위해선 어떻게 코드를 짜야할까?

• 재귀호출하여 S가 0이 되는 것들과 아닌 것들을 구분해야 한다 (Y에 담겨있느냐 없느냐)
• i번째에서 답을 찾았는지 검사한다. (S ==0, S < 0)로. 답을 찾았다면 []를 리턴하고 찾지 않았다면 아무것도 None.
• i번째에서 답을 찾지 못했다면 i-1 을 탐색한다. 먼저 담지 않은 경우가 답이 되는지 보고 답이라면 (None 이 아닌 것을 반환한다면) 담지 않은 대로 그대로 Y를 올린다.
• 담은 경우가 답이라면 올라온 Y에 A[i] 을 더한 것을 리턴한다
• 포함, 불포함 모두 답을 못찾았으면 None
  

🔨 Subset sum - DP로 풀기

따라서 위 문제는 다음과 같이 나타낼 수 있다.

Subsetsum(A, i, S) 의 하나의 문제를, Subsetsum(A, i-1, S-A[i]) 과 Subsetsum(A, i-1, S) 중 선택하는 문제로 바꾼 것이 아닌가? (i와 i-1 간 부문제로 전환)

DP테이블을 쓰면
DP[i][S] = DP[i-1]S-A[i]] or DP[i-1][S]

(i,S)를 결정함에 있어 바로 위 행인 i-1 의 S-A[i] 열(바로 위에서 A[1] 거리만큼 이동) 또는 S 열 (바로 위) 의 or 연산이 된다. 복잡도는 역시 격자 크기인 n, S를 곱한 O(ns)가 되나 이는 Pseudo Polynomial algorithm 에 속한다.

왜? O(2^n) 과 비교했을 때 O(ns)는 n이 작고 s가 기하급수적으로 클 때 훨씬 시간이 오래 걸리기 때문이다. (주어진 숫자 4개, 합이 10^1000 경우)

🔨 Subset sum - Backtracking 으로 풀기 (1)

만약 주어진 배열이 A = {8, 6, 7, 5, 3, 10, 9} 이고 S = 15일 때 포함하는 수를 1, 하지 않는 수를 0으로 표기하면 x = [0, 0, 1, 1, 1, 0, 0] 이 하나의 답이 될 수 있다. 이걸 어떻게 구현할까?

백트래킹으로 보는 코드를 우선 먼저 보자. 수도코드.

SubsetSum_backtrack(k): # x[k] = 0,1 결정하는 함수, x[0]부터 x[k-1]은 이미 결정이 났음.
	current_sum = sum(A[i] * x[i] for i in range(k)) # 전체 A[i] 주어진 숫자에서 x[i] 가 1이라면 뽑혀서 더해지는 것. 현재까지의 합을 우선 계산 
    if k==|A|:
    	if current_sum == S:
        	print(x) # k가 끝까지 왔을 때 검사, 만약 합이 S와 같다면 출력
    else: # 아직 끝까지 안 온 경우 
    	if current_sum + A[k] <= S: # 현재의 합에서 하나를 더 더해보고 S보다 작으면 
        	x[k] = 1 # 표시하고 (포함한다는 뜻) 
            SubsetSum_backtrack(k+1) #k+1 로 넘어감
        # 표시, 표시 하며 갔는데 합이 나오지 않은 경우 = 0 으로 이번엔 포함하지 않음
        x[k] = 0 
        SubsetSum_backtrack(k+1) 

먼저 가장 큰 if...else 문은 k가 끝까지 갔는지를 검사하는 것이고, 끝까지 갔다면, 그 중에서도 현재의 합이 정확히 S라면 출력한다.

그렇지 않다면 남은 수들이 있다는 것으로 또 한번의 if 문을 추가한다. 만약 현재의 합에 A[k] 를 추가해도 S를 넘지 않는지 확인한다음, 넘지 않으면 1로 바꾸고 다음 단계로 계속 진행하는 것이다. (어느순간 합이 넘어갈 때 재귀적으로 호출하는 것을 중단할 것이다.)

중단된다면 A[k] 를 더했을 때 숫자가 넘는 경우이므로, 이번엔 if 문에서 탈출하여 x[k] = 0 포함하지 않는 경우를 만들고 k+1 재귀호출한다.

🔨 Subset sum - Backtracking 으로 풀기 (2)

거의 비슷한 방법이지만 정렬 추가 + 인덴트만 다르게 함으로써 이득을 볼 수 있다.

예컨대 위와 같은 방법에서 정렬을 추가하면
A = {3, 5, 6, 7, 8, 9, 10} 이 되고, S= 15일 때 코드에서 하라는대로 하면

x = [1, 1, 1] 을 추가하다가 7을 추가하려할 때 숫자가 넘었으므로 7은 0으로 표시하고, 8, 9, 10 을 또다시 검사할 것이다. 그러나 이는 검사할 필요가 없다!

왜냐하면, 정렬된 상태이므로, 7을 넣었을 때 합을 넘는다면 그 이후의 수들은 무조건 합을 넘는다고 볼 수 있어서 탐색이 의미가 없기 때문이다.

# A는 정렬된 상태로 만ㄷㅡㄴ다. 
SubsetSum_backtrack(k): # x[k] = 0,1 결정하는 함수, x[0]부터 x[k-1]은 이미 결정이 났음.
	current_sum = sum(A[i] * x[i] for i in range(k)) # 전체 A[i] 주어진 숫자에서 x[i] 가 1이라면 뽑혀서 더해지는 것. 현재까지의 합을 우선 계산 
    if k==|A|:
    	if current_sum == S:
        	print(x) # k가 끝까지 왔을 때 검사, 만약 합이 S와 같다면 출력
    else: # 아직 끝까지 안 온 경우 
    	if current_sum + A[k] <= S: # 현재의 합에서 하나를 더 더해보고 S보다 작으면 
        	x[k] = 1 # 표시하고 (포함한다는 뜻) 
            SubsetSum_backtrack(k+1) #k+1 로 넘어감
        	# 표시, 표시 하며 갔는데 합이 나오지 않은 경우 = 0 으로 이번엔 포함하지 않음
        	x[k] = 0 
        	SubsetSum_backtrack(k+1) 

위의 코드는 if current_sum + A[k] <= S 비교하는 코드가 x[k] = 1 포함하는 것에만 적용되어 있어 만약 수가 넘는다면 포함하지 않는 x[k] = 0 코드를 무조건 다 수행해줘야 했다. 근데 그럴 필요가 없다는 것이 결론이었고 쉽게 x[k] =0 코드 역시나 위의 if 문 안쪽으로 밀어넣어주면

• 먼저 x[k] 해당 숫자를 넣어도 합이 넘지 않는지 검사한다, 넘지 않으면
• x[k] = 1 포함한 재귀호출과 x[k] = 0 포함하지 않은 재귀호출 둘 다 한다
• 어떤 호출에서 합이 넘으면 그 아래 호출은 더이상 하지 않고
• 이미 호출되었지만 그 아래로 먼저 내려가느라 수행되지 않았던 다음 호출을 수행한다.
• A[k] 가 정렬되었을 경우 할 수 있는 것으로써 A[k] 숫자를 더해봤는데 합이 넘는다면 해당 A[k]를 실제로는 포함하지 않더라도 A[k+1] 등 언젠가 넘어버릴 것임을 확정할 수 있으므로 아예 그곳에선 탐색을 중단한다는 것이다.
  

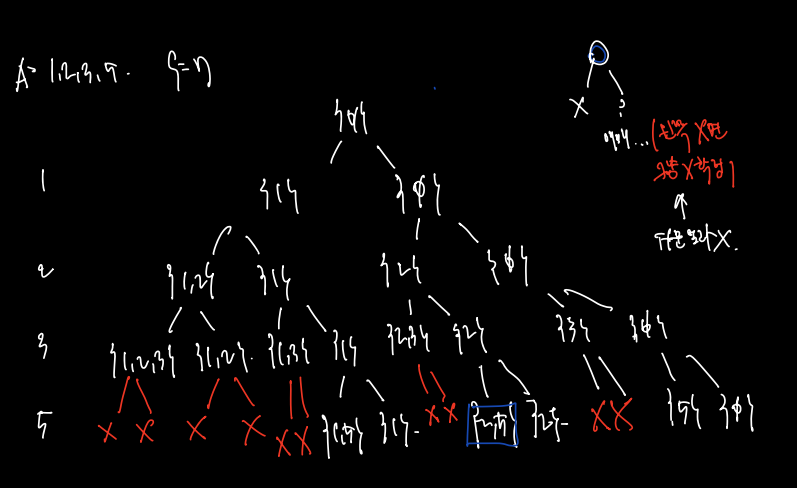
다음과 같이 아낄 수 있다는 것이 포인트다. 직접 그려보자.

• 왼쪽 tree가 안되면 자동으로 오른쪽도 지우자
• 시간복잡도 O를 확정할 수 없다.

🔨 Sudoku

아이디어는 간단하다.

• 순회하며 0인 칸을 찾고, 1-9까지 넣을 수 있는지 검사해본다. (행, 열, 3X3 이내에 같은 수가 존재하지 않는지 검사하는 함수), 넣을 수 있다면 채우고, 넣을 수 없다면 backtrack
• 다시 0인칸을 찾고, 1-9까지 검사하고, 채운다. >> 반복!

교과서의 코드를 한 번 살펴보자!

• 필요한 함수는 2개로 빈칸을 찾아 row, col 을 반환하는 함수 (빈칸이 없다면 풀음)
• is_safe 는 A 주어진 스도쿠의 행, 열에 num 숫자를 넣어도 되는지 검사하는 함수이다
• 1, 10까지 숫자의 후보를 보며 넣을 수 있다면 숫자를 넣고 재귀호출한다.(True 라면 True 를 반환하도록 if 문에 넣었다.)
• 만약 후보를 다 돌았는데 들어가지 않는다는 건 backtrack 이 필요한 상황이므로 해당 행, 열을 0으로 만들고 False 를 리턴한다.
• 그러면 그 전 호출에서 다른 숫자를 넣어볼 것이다.

복잡도는 각 칸에서 1-9 를 선택하고, 이러한 결정을 81번(9X9 격자일 경우) 반복하므로 9^81 이나 Big-O O(1) 임!

🔨 Knapsack Problem

• 15L만 견디는 배낭이 있고
• 물건의 크기와 가격이 있을 때
• 물건의 가격이 최대가 담도록 배낭에 담는 경우를 반환

유형은 2가지다.
1. 0/1 문제: 선택한 물건은 전체 다 넣는 문제
2. fractional 문제: 쪼개서, 원하는 만큼 넣는 문제 (단위 무게당 비싼 것부터 넣고, 넘치면 잘라내자!:(Greedy를 사용하면 된다.)

우리는 2를 풀 때 Greedy 방법으로 풀 것이다.
가격 40, 30, 50, 10 이 주어지고
크기 2, 5, 10, 5 가 주어지면 가격을 크기로 나눴을 때
가성비 20, 6, 5, 2 가 된다는 것을 알 수 있으므로,

가방의 크기 k = 16이라 하면
우선 크기 2짜리 (20), 크기 5짜리 (30), 크기 10짜리 (50) 을 넣을 때 17이 되므로 크기 10을 9만큼만 줄여 (가격도 50 > 45) 넣는 방법을 생각해볼 수 있다.

이 외에도 0/1 문제는 Greedy와 backtrack 중 backtrack 를 선택하는 것이 현명하다.
grredy로 풀 경우 경우 가성비가 좋은 순서대로 넣다가, 넘치면 다음 것을 넣는 방법을 사용하면 되므로 40, 30, 10이 들어갈 것이다. backtrack 모든 가능한 경우의 트리를 차례로 방문해보고, 가장 좋은 선택을 계산한다. (40 + 50 = 90이 될 것이다.)

문제 자체를 비교하면 당연히 Fractional >= 0/1 의 답일 것이다. 왜? 말그대로 잘라서 넣고 greedy니까 0/1이 제시한 답을 모두 fractional 로 바꿀 것이다.