활성화 함수 (Activation Function)
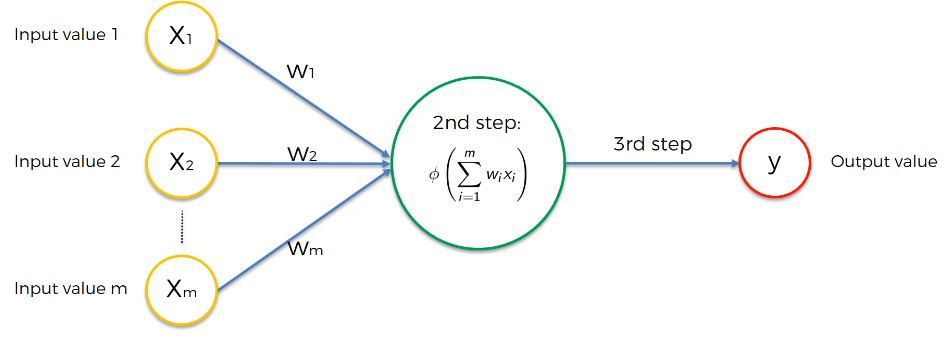
하나의 뉴런의 모습이다.
활성화 함수의 4가지 유형을 알아보자.
임계함수 (Threshold Function)
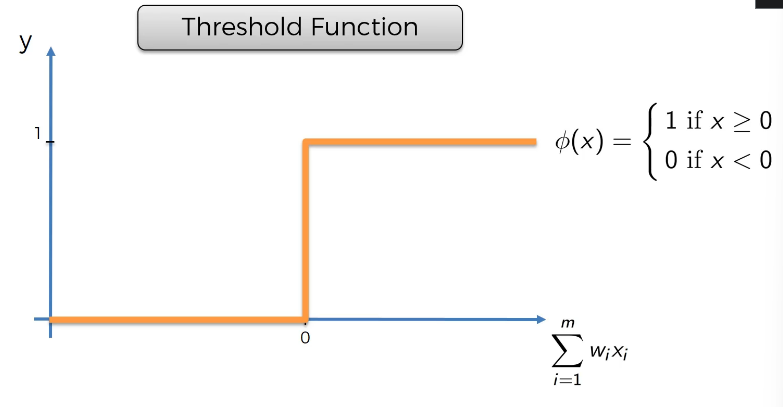
x축 인풋으로 들어오는 것은 입력값의 가중합이다. (모르겠다면 활성화함수 위를 보고오자.) y 축에는 0부터 1까지 값이 있다. 값이 0보다 작으면 0, 0보다 크면 1을 내보낸다. 예, 아니오만 있는 함수이며, 다른 옵션은 없다.
시그모이드함수 (Sigmoid)
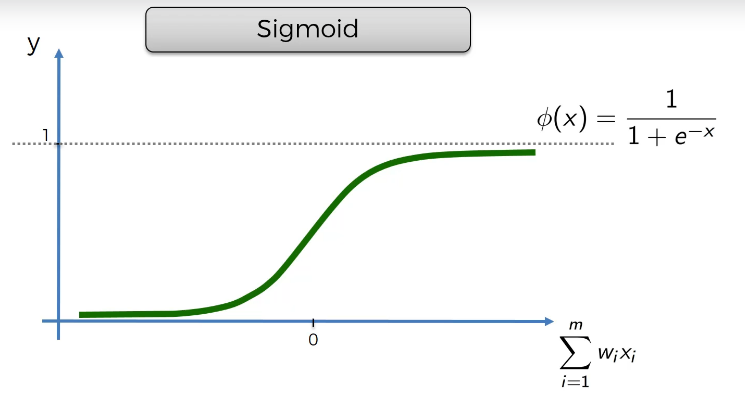
1을 1+e^(-x) 로 나누는 것이다. x는 역시나 가중합이다. 임계함수와 달리 부드럽다는 점이 장점이다. (점진적 진행) 시그모이드 함수는 출력층, 마지막 층에서 유용하다.
렐루 함수 (Rectifier)
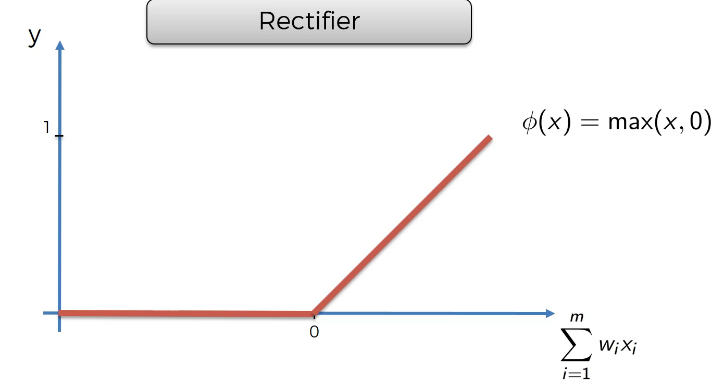
x,0 중에 큰 값을 고르기 때문에 x가 음수면 무조건 0이고 양수면 무조건 x 값을 따른다. (꺾임이 있다.) 렐루함수가 인공신경망에서 가장 많이 쓰이는 함수이다!
쌍곡선 탄젠트 (Hyperbolic Tangent)
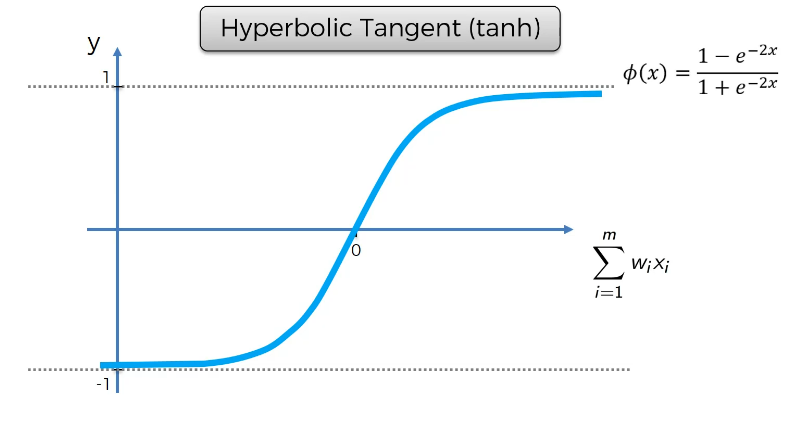
시그모이드 함수와 유사하지만 쌍곡선 탄젠트는 0아래로 내려간다. -1까지, 1까지 근접한다.
예컨대 이진형 변수에서는 임계활성화 함수를 쓰거나(이게 베스트다.), 시그모이드 활성화 함수를 사용할 수 있다. 시그모이드는 완전한 0과1은 아니지만 0과 1을 출력할 확률을 구하는 활용할 수 있다. (위로 올라갈수록 1을 출력할 확률이 더 높은 것)
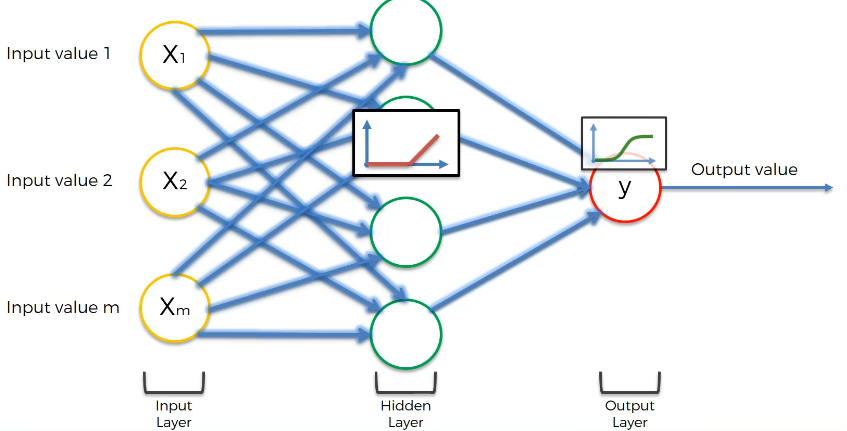
첫 입력층의 인풋이 첫 은닉층으로 전달되면 활성화 함수가 적용된다. 여기서 렐루 함수를 적용시킨다.(은닉층: 렐루) 렐루 함수를 적용한 신호는 출력층으로 전달되고, 출력층에는 시그모이드 함수를 사용한다. (출력층: 시그모이드) 시그모이드가 출력한 0과 1 사이 값이 최종 출력값이 된다. (예컨대 확률에측)
이제 활성화 함수의 유형을 알았으니 실제 활용을 해보자! (편하게 사용하는 것이 목표)
신경망의 원리 (NNs Work)
그렇다면 신경망은 어떻게 사용될까?
주택 평가 사례를 보자.
주택 가치의 매개변수를 포함하여 주택을 평가하는 신경망을 살펴보자! (훈련을 마쳤다고 가정한 신경망)
입력매개변수가 4개 있다. (면적, 방의 개수, 가장 가까운 도시 거리, 주택 나이) 4가지 매개변수는 입력층을 구성한다. 은닉층은 없다고 가정하고, 주택 가격인 출력층만 있다고 하자. 입력 변수의 값을 시냅스로 가중해서 출력값을 계산하자.
예컨대 가격을 모든 입력값의 가중합처럼 간단히 계산할 수 있다.
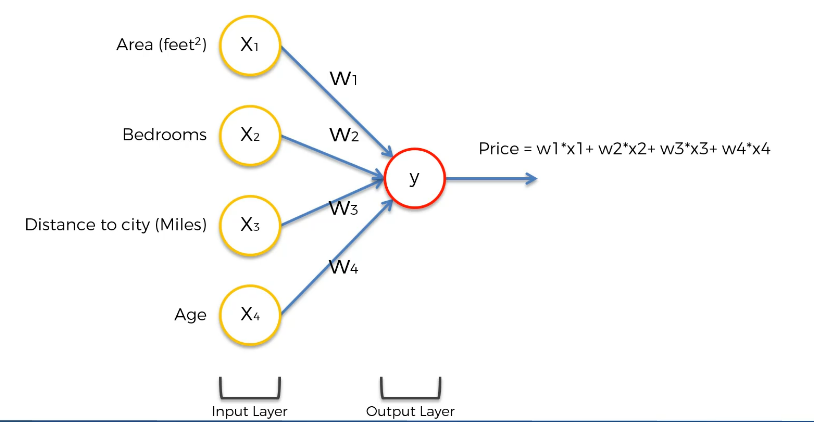
여기서 앞서 살펴본 아무 함수나 사용할 수 있다. (특정 출력값을 얻으면 됨!)
대부분의 머신러닝 알고리즘은 다음과 같이 신경망으로 표현할 수 있다. (변수와 가중치, 가중합, 은닉층 없이도) 그러나 추가로 인공신경망이 하는 것은 유연성을 제공하는 것인데, 이때 정확도를 증가시키는 것이 은닉층이다.
은닉층이 어떻게 힘을 부여할까?
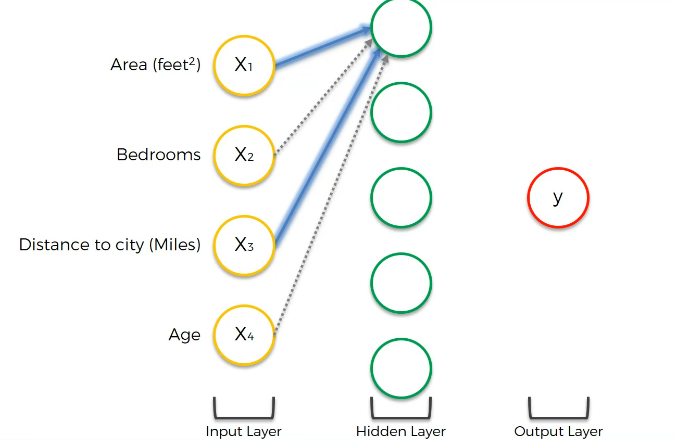
매개변수 4개와 은닉층 맨 위의 뉴런의 관계를 살펴보자. 입력층의 뉴런에는 모두 시냅스가 있는데, 이 시냅스가 모두 은닉층의 첫 뉴런과 연결된다. 이때 어떤 시냅스, 가중치는 0일 수 있다. (입력값이 중요하지 않은 경우) 예컨대 첫 뉴런에 면적과 거리가 연결되고 나머지는 0이라 하자. 왜 면적과 거리는 연결될까? 도시에서 멀어질수록 가격은 내려가고, 면적은 커질 것이다. 이때 (반대로) 뉴런은 도시에서 멀지 않으면서 면적이 큰 주택을 노린다. 그러한 특정 주택을 골라내어 활성화를 하고, 이때 활성화 함수가 나온다. 특정 기준에 도달하면 활성화 한다. (스스로 계산 수행) 변수를 조합하여 출력층의 가격에 기여한다. (면적과 거리를 고려하는 뉴런, 새로운 매개변수, 새로운 속성)
또 하나의 예로, 중간의 뉴런은 면적, 방의 개수, 나이를 고려한다고 해보자. 이 데이터로 알아낼 수 있는 것은 무엇일까? 수천 주택 사례 중 면적 + 침실 + 나이가 중요한 것을 안 것이다! 방이 많은, 신축인, 넓은 주택을 찾고 있을 것이다. 신경망이 훈련을 거치면서 면적이 넓고 방이 많은 집이 시장에서 가치가 있다는 것을 알고 그런 것을 고르는 것이다! (새로운 매개변수)
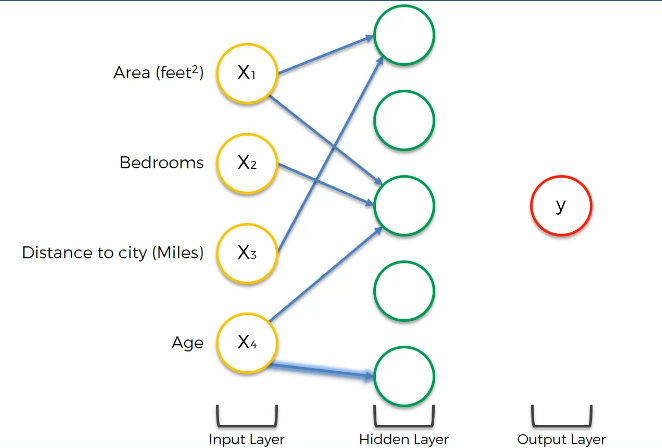
제일 아래쪽 뉴런은 변수 하나만 고른다고 하자. 나이만! 오래된 주택은 낡아서 가치가 떨어진다. 새 건물의 경우는 좀 더 비쌀 수 있다. 주택이 특정 나이를 넘어서면 고택이 되기도 한다. 고택에 가치를 더 주는 사람들도 있다. 이 뉴런은 100년이 넘는 집을 발견하면 발화해서 가격에 기여한다. (렐루함수를 떠올려보자. 0에서 100년까지는 0의 값을 가지고 있다가 100년이 넘으면 오래될수록 가격에 기여하는 정도가 증가한다.)
이 외에도 신경망은 우리가 생각지 못한 관계를 추출하기도 한다. (기존 FE와 공통되면서 차이가 나는 부분) 따라서 은닉층이 유연성을 증가시키고, 데이터 중 특정 대상을 찾아 정확도를 증가시키는 데 기여하는 것이다.