신경망의 학습법 (NNs learn)
- 하드코딩: 규칙 지정, 전 과정을 지도하면서 가능한 옵션을 모두 설명
- 신경망 학습: 신경망에게 입력값, 출력값을 준 다음 스스로 모든 것을 알아내게 함.
개와 고양이를 구분한다면, 하드코딩은 얼굴형, 색, 몸집, 귀 등을 설명해주고 규칙과 조건을 지정해주는 것이다. 신경망학습은 개, 고양이 이미지를 주고 스스로 학습하게 하는 것이다.
우리가 지금까지 본 그림은 단층 순방향 신경망이라고 한다. = 퍼셉트론.
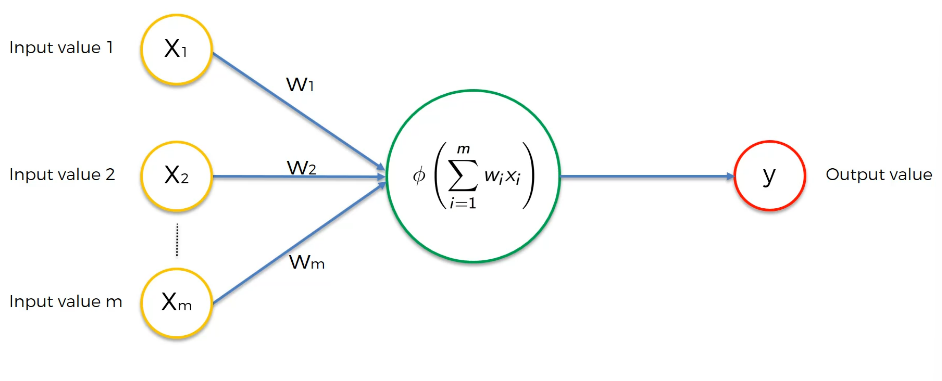
이제 y를 y'(y-hat) 로 바꿔주자. 실제 y 와 y'의 차이를 계산한다. (제곱하여 반으로 나누는 비용함수를 쓰자) 이것으로 비용함수가 구성되고, 목표는 비용함수를 최소화하는 것이다. 다시 이 정보를 신경망으로 공급하면 가중치로 이동하고 업데이트된다. 다시 값들을 신경망에 공급, 비용계산, 가중치 업데이트의 과정을 반복한다. (같은 행에서 다룬다는 점에 주의하자.)
만약 여러 행을 다룬다면 다음과 같이 여러개로 표현할 수 있다. (퍼셉트론은 하나다! 동일한 퍼셉트론에 행만 여러개다.)
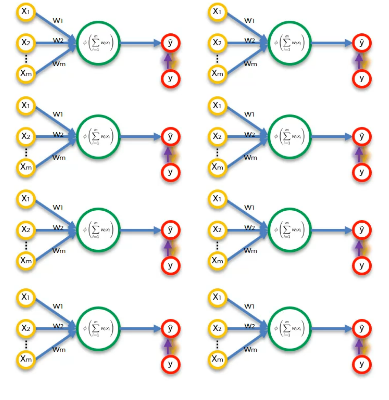
8개 값이니 다음과 같은 8개의 y'을 얻는다. 그리고 실제값과 비교한다. (각 행마다 실제값이 존재한다.)
역시나 비용함수를 가지고 각각의 가중치를 업데이트한다. (퍼셉트론 하나이므로 가중치도 딱 3개이다.) 비용함수가 최소화되면 최종 신경망이 완성된다. 데이터세트에 최적인 가중치를 찾았다는 뜻이고, 다음 단계로 나아갈 준비가 되었다는 것이다. 오차를 보고 뒤로 돌아가 가중치를 업데이트 하기 때문에 이 과정을 역전파라고 한다.
Gradient Descent
그렇다면 가중치는 정확히 어떻게 업데이트될까?
- 무차별 대입법 : 아무 가중치나 대입, 적은 비용을 확인하는 것이다.
가중치 수가 커질수록 시냅스 수도 커지므로 차원의 저주가 일어난다.
차원의 저주란 무엇인가?
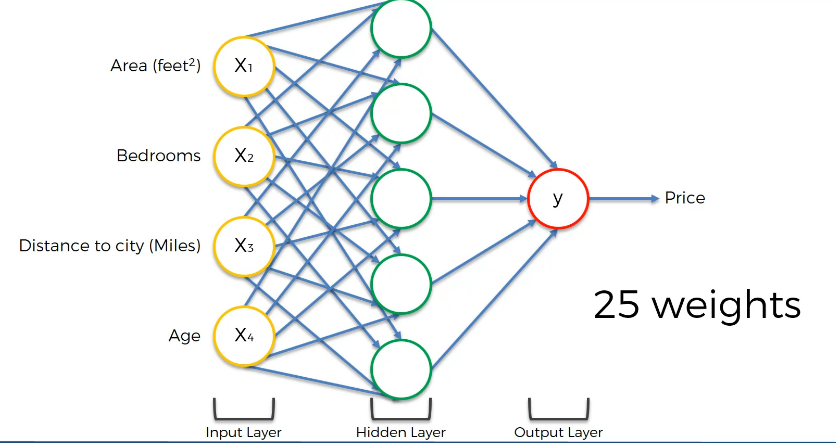
가중치는 하나의 시냅스와 같으므로, 위와 같이 은닉층이 개입되면 가중치 또한 늘어난다. 아래 그림에선 25개의 가중치, 즉 시냅스가 있다.
-
여기에 대입으로 숫자를 때려넣으면 너무 많은 시간이 걸린다.
-
경사하강법은 손실함수를 미분을 해서 알아낸 기울기를 본다. 기울기의 양, 음을 보고 하강하는 방향으로 업데이트를 한다.
-
지그재그로 내려오면서 손실을 최소화한다.
-
이렇게 내려오면 무차별 대입하는 것보다 빠르게 최적화가 가능하다. (길이 있으므로)
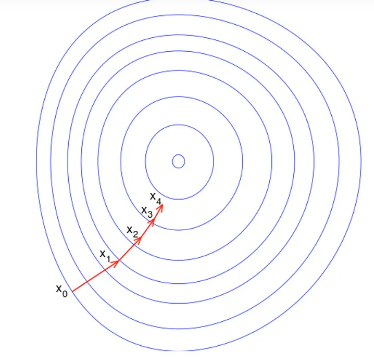
-
2차원 등고선으로 표현한 경사하강법은 다음과 같다. (파라미터2개)
확률적 경사하강법 (Stochastic Gradient Descent)
그런데 우리가 봤던 비용함수의 형태가 꼭 저렇게 정직하게 볼록하지 않다면 어쩔 것인가?

비용함수가 다차원 공간에 있거나 y'-y 를 제곱하고 1/2 한 값이 아니고 다른 함수를 선택한다면 실제로 가능한 모양이다. 이와 같은 계형에서 경사하강법으로 최적화를 진행하면 최솟값이 아닌 극솟값을 찾게 된다. 이때 확률적 경사하강법을 사용한다.
확률적 경사하강법과 일반적인 경사하강법의 차이는 가중치 조정의 타이밍이다. 본래 가중치 조정은 일반적인 경사하강법의 경우 모든 행에 따른 오차를 계산한 후에 진행되었으나 확률적 경사하강법은 한 행의 오차를 계산하고 난 다음 바로 가중치 조정을 실행한다. (행 하나마다 가중치 조정)
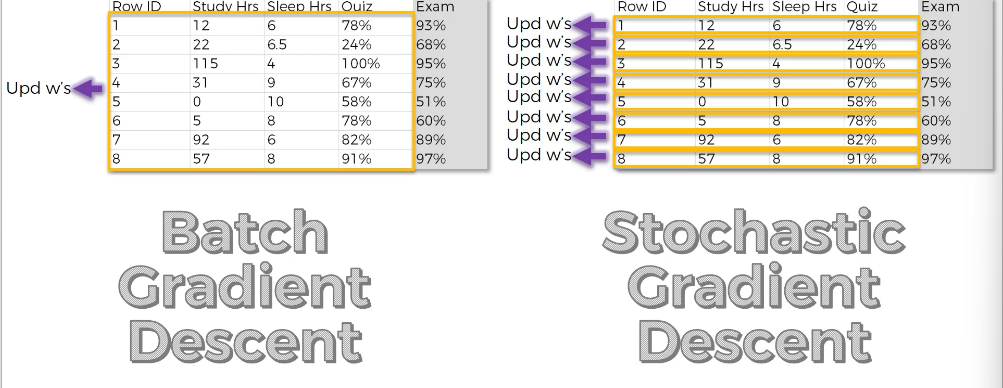
확률적 경사하강법은
- 극값, 극소값을 피하고 최솟값으로 간다.
- 변동이 훨씬 크다. (행에 따라 조정하기 때문에)
- 더 빠르다. (모든 행의 실행까지 기다릴 필요가 없다.)
이러한 장점이 있지만 확률적 경사하강법은 그야말로 확률론적 방식이므로 업데이트 할 때마다 다른 과정, 다른 반복을 거쳐 도달하게 된다. (행을 랜덤으로 뽑는다.) 경사하강법은 그렇지 않아 많이 사용하는 것이다.
미니 배치 경사하강법은 행을 10, 100개로 묶어 그 단위로 가중치를 업데이트 한다. (둘의 중간!)
역전파 (Backpropagation)
순전파라는 과정에서 순방향으로 입력층, 은닉층, 출력층, 오차 계산으로 게산되면 신경망을 통해 역방향으로 가며 가중치를 업데이트한다.
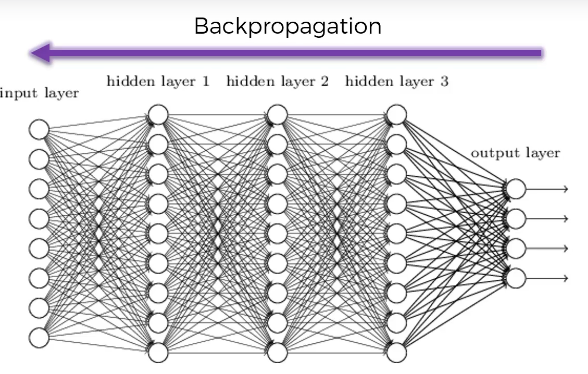
역전파의 핵심은 알고리즘이 구성된 방식 하나만으로 모든 가중치를 동시에 조정해서 각 가중치가 어느 부분의 오차에 원인 제공을 했는지 알 수 있다는 것이다. (모든 가중치를 동시에 조정한다는 특장점)
신경망 훈련의 과정
- 가중치를 0에 근사하지만 0이 아닌 수로 초기화 (임의의 값)
- 첫 관측치를 입력층에 넣는다, 각 피처를 각 노드에.
- 순전파: 왼쪽에서 오른쪽으로 뉴런을 활성화한다.
- y예측값과 실제값을 비교하고 오차를 발생시킨다.
- 역전파: 오른쪽에서 왼쪽으로 오차가 역진행한다. 오차에 따라 가중치를 업데이트한다. 학습률은 가중치를 어디까지 업데이트하는지 결정.
- 1-5를 반복. 관측치 분량마다 가중치를 업데이트
- 비용함수 최적화까지 이를 반복수행한다.