[핸즈온 머신러닝] 11. 심층 신경망 - Optimizer

고속 옵테마이저

훈련 속도를 높이는 방법은 현재까지 알아본 방법으로 가능하다.

• 가중치의 초기화 방법
• 좋은 활성화 함수
• 배치 정규화
• 사전 훈련된 네트워크 일부 재사용

이 외에도 훈련 속도를 높이려면 최적화 방법을 다르게 사용할 수 있다. (더 빠른 최적화 방법으로)

따라서 모멘텀 최적화 / 네스테로프 가속 경사 / AdaGrad / RMSProp / Adam / Nadam 옵티마이저를 알아볼 것이다!

1. 모멘텀 최적화

표준적인 경사하강법은 경사면이 있다면 일정한 크기의 스텝으로 조금씩 내려간다. 그러나 모멘텀 최적화의 경우 모멘텀, 즉 관성을 이용하겠다는 의도를 가져 처음에는 느리게 출발하지만 종단속도에 도달할 때까지 가속한다.

기존 경사하강법은 다음과 같았다.

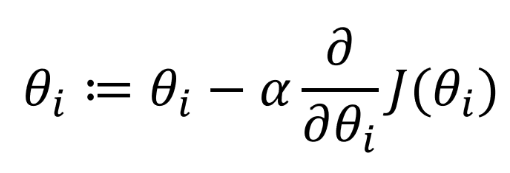
비용함수 J가 있다면 비용함수를 해당 업데이트 대상에 대해 편미분 한 값을 기존 업데이트 대상에서 빼주면 1Step 간 것이다.

• 현재 위치에서 미분만 하고 이전 그레디언트는 고려하지 않는다
• 그레디언트가 작으면 매우 느려진다
• 지역 최적화의 가능성이 있다

모멘텀 최적화는 이전에 진행되어왔던 방향을 한 번 더 계산해주기 때문에 다음의 문제를 해결할 수 있다.

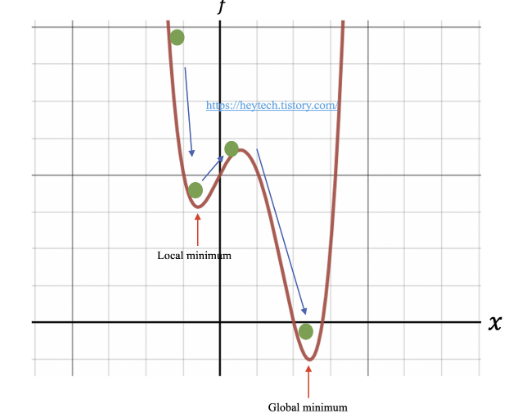
처음 계산된 그레디언트로 최적화를 반복하다가 local minimum 에 빠질 수 있었지만 여기서 모멘텀을 이용하면 내려오던 방향이 있으므로 탈출이 가능하다. 다음 내려갈 때는 관성을 받아도 탈출하기에 쉽지 않으므로 결과적으로 Global minima 에 도달했다고 말할 수 있다.

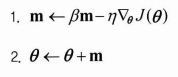
책에 나온 것은 다음과 같은 식이지만 시간 스탬프가 반영되어 있는 다음 식을 보자.

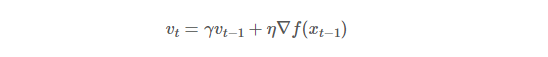
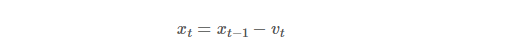
• v는 t번째 시간에서 x의 이동벡터를 계산해준 값이다.
• r은 관성계수이다. 이동벡터도 연속된 값을 가지며 변화하는데 그 이동 벡터에 얼마만큼의 가중치를 줄 것이냐 하는 것. (0.9 ~ 1 사이에서 결정)
• 에타는 그레디언트 계산한 값에 붙이는 학습률을 뜻한다.

t번째 x 값을 계산하기 위해서 필요한 건 기존 t-1 의 x 값과 t시점의 이동 벡터이다. 이동벡터는 이전에 움직였던 값을 기억해 한 번 더 계산해주기 위함이므로, 본래 그레디언트만 있다면 일반적인 SGD 와 같겠지만 거기다가 이전 이동 벡터를 한 번 더 더해주는 것이다. (이동벡터가 연쇄적으로 연결되어 있으므로 이전 그레디언트가 모두 담겨있다.) 이 값을 업데이트할 때 최종적으로 빼주면 된다!

케라스에서 구현하는 방법은 기본 SGD 옵티마이저에 + 모멘텀 변수를 지정하는 것이다.

![](https://velog.velcdn.com/images/kyungmin1029/post/5a38a4ed-fe4e-4e9b-99e6-8db0fb2dae81/image.png)

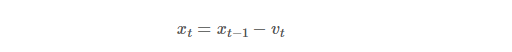
optimizer = keras.ooptimizers.SGD(learning_rate = 0.001, momentum = 0.9) 

2. 네스테로프 가속 경사

기존 모멘텀 최적화보다 항상 더 빠른 최적화 방법이다.
그레디언트의 미분을 세타가 아닌 세타에 이동벡터 * 관성계수를 곱해준 값에서 계산해주는 방법을 사용한다.

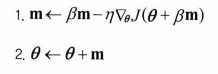
• 기존 모멘텀 알고리즘의 아이디어와 같이 그레디언트와 이동 계수를 더한 값을 함께 업데이트에 사용했다
• 그레디언트를 계산할 때 세타가 아닌 모멘텀이 반영된 곳에서 계산해주는 것!

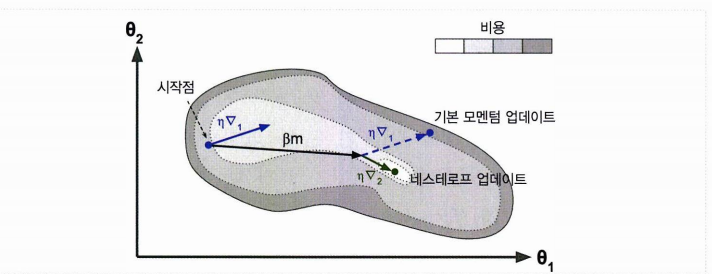
1. 기본 모멘텀 업데이트의 경우 기존위치에 + (관성계수 이동벡터) + 그레디언트 값
2. 네스트로프 업데이트의 경우 기존위치에 + (관성계수 이동벡터 값) + 나아간 위치에서 그레디언트

• 기본 모멘텀보다 속도가 빠르고
• 진동을 감소시키고 수렴을 빠르게 한다

optimizer = keras.optimizers.SGD(learning_rate = 0.001, momentum = 0.9, nestrov = True) 

3. AdaGrad

AdaGrad 알고리즘은 가장 가파른 경사가 아닌 가장 가파른 차원을 따라 그레디언트 벡터의 스케일을 감소시킨다. 차원은 곧 feature 이므로, feature 별로 학습률을 Adaptive 하게 조절한다고 하며 AdaGrad 라는 이름을 붙였다.

역시나 학습률의 의미가 담긴 다른 식을 보겠다.

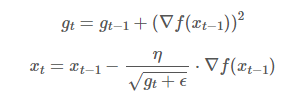
1. 그레디언트 제곱을 g에 누적한다.
   : 비용함수가 i번째 차원을 따라 가파르다면 해당 g_i 가 상대적으로 점점 더 커지게 만든다

2. 경사하강법과 비슷하나 그레디언트 벡터를 g + e 로 나누어 스케일을 조정한다. / 학습률이 (에타 / g + e) 이다.
   : 큰 기울기를 가져 학습이 많이 된 변수는 학습률을 감소시킨다.

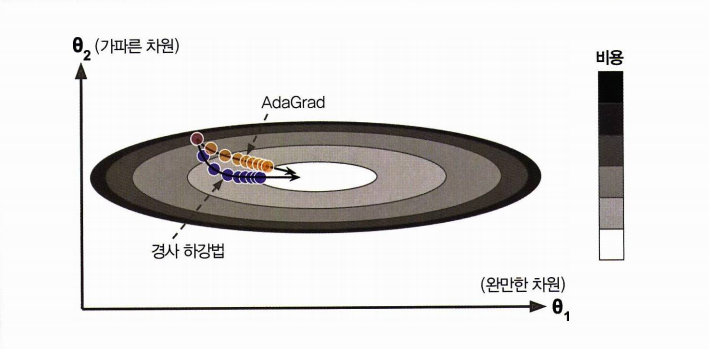
• 이렇게 경사가 완만한 차원보다 가파른 차원에 대해 더 빠르게 감소되는 것을 적응적 학습률이라 할 수 있다.
• g_t 값이 점차 커지므로 학습률 에타 / g+e값도 너무 빠르게 감소되어 알고리즘이 완전히 멈출 수 있다.
• 학습이 잘 이루어져 업데이트 되지 않는 것인지, g값이 지나치게 커져서 학습이 멈춘 것인지 헷갈린다.

4. RMSProp

AdaGrad 의 학습이 너무 빨리 멈추는 문제 (g가 커지고 학습률이 빠르게 감소)를 해결하기 위해 등장했다.

AdaGrad 는 g를 계산할 때 이전까지의 모든 그레디언트 제곱값을 누적했지만 RMSProp 의 경우 최근 그레디언트만 누적하는 방법을 사용했다! 기울기를 같은 비율로 누적하지 않고 지수이동평균(EMA) 를 사용하여 기울기를 업데이트한다. => 최근의 기울기는 많이 반영하고, 먼 과거의 기울기는 조금만 반영하자!

time 을 반영한 식을 보자.

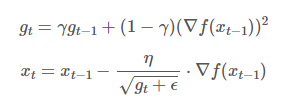
• g_t 는 t번째 시간까지의 기울기 누적 크기를 의미한다
• r은 지수이동평균의 업데이트 계수를 말한다.

t번째 누적 기울기의 경우 현재까지의 누적 기울기 (g_t-1)에 r을 곱해 의도적으로 작게 만들어준다. / 동시에 새로운 그레디언트는 1-r 을 곱한 값을 더하여 업데이트 한다.

• 변수마다 학습률을 적용할 수 있다는 점
• AdaGrad 보다 학습을 오래하여 최적에 도달할 수 있다는 점의 장점이 있다.

코드는 다음과 같다.

optimizer = keras.optimizers.RMSprop(learning_rate = 0.001, rho = 0.9) 

5. Adam, Nadam

Adam(Adaptive moment estimation) 은 모멘텀 최적화와 RMSProp 의 아이디어를 합친다.

• 모멘텀 최적화의 지난 그레디언트의 지수 감소 평균을 사용하고

• RMSProp의 지난 그레디언트 제곱의 지수 감소된 평균을 따른다.
  

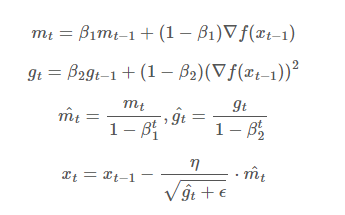
• 베타는 EMA 로써 하이퍼파라미터이다. 일반적으로 베타1(모멘텀의 지수이동평균)은 0.9, 베타2(RMSProp의 지수이동평균)가 0.999가 가장 좋은 값이라고 알려져 있다.

• m_hat, g_hat 은 처음 학습을 시작할 때 m_t-1, g_t-1 이 0이고, 각 그레디언트가 너무 작기 때문에 값을 증폭시켜 줘서 구하기 위한 장치이다.

• 학습이 진행되다 보면 1-B1, 1-B2 는 거의 1에 가까워지기 때문에 결국 m_hat 와 g_hat 은 각각 m, g 와 같은 값이 된다.

코드를 보자.

optimizer = keras.optimizers.Adam(learning_rate = 0.001, beta_1 = 0.9, beta_2 = 0.999) 

Nadam
Nadam 은 Adam + 네스테로프를 적용한 것이다. 때때로 Adam 보다 좀 더 빠르게 수렴하는 것을 확인할 수 있었다.

추가로 적응적 최적화 방법(RMSProp, Adam, Nadam) 이 빠르게 수렴하지만 일부 데이터셋에서 성능 자체가 떨어지는 것을 논문 등에서 확인할 수 있었다. 따라서 모델 성능이 문제일 경우 네스테로프 가속을 사용해보자! (연구 결과를 더 확인하자.)

6. 학습률 스케줄링

실제로 어떤 최적화 방법을 사용하는지만큼 좋은 학습률을 찾는 것도 매우 중요하다.

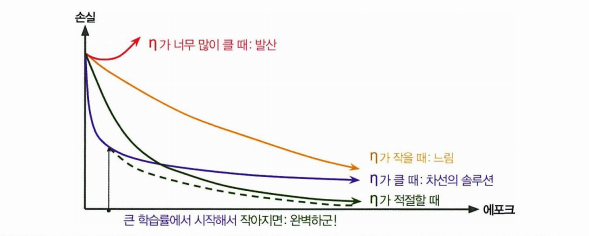
일정한 학습률보다 더 나은 방법들을 생각해보자. 큰 학습률로 시작하고 학습 속도가 느려질 때 학습률을 낮추면 해에 더 빨리 도달할 수 있다. 이런 전략들을 학습 스케줄이라 한다!

1. 거듭제곱 기반 스케줄링
   
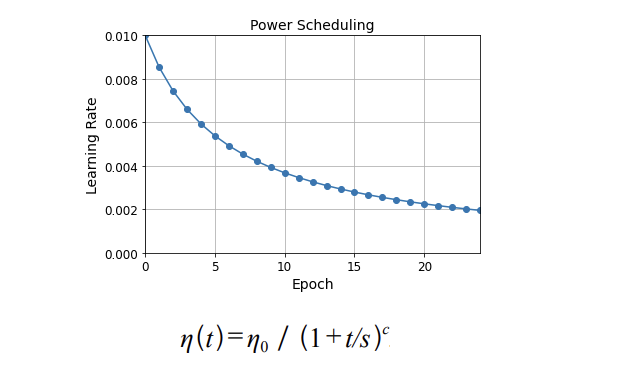
   초기 학습률 에타 / 거듭제곱 수 / 스텝횟수(고정) / 반복횟수 t 학습률은 t 에폭이 늘어나면서 감소된다.

2. 지수 기반 스케줄링

• t: Training epoch
• s: 스텝 횟수
  t가 늘어날 때마다 학습률이 감소되는 방식이다.

3. 구간별 고정 스케줄링
   

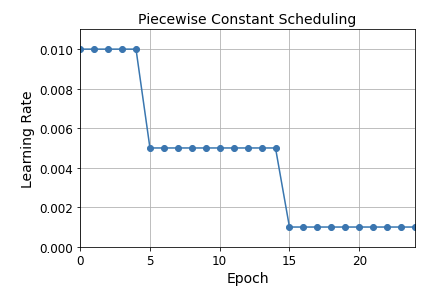
에폭에 따라 학습률을 구간별로 정의하는 것이다. 그림을 보면 이해가 쉽다. (최적 조합은 우리가 찾아야 한다.)

4. 성능기반 스케줄링
   

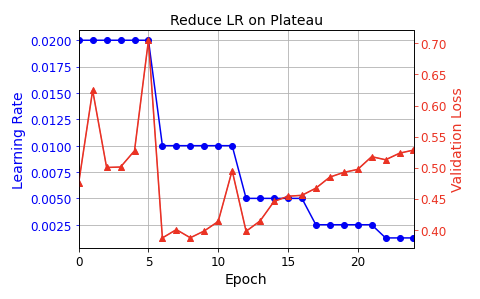
N번의 스텝마다 Validation Loss 를 측정한다.(붉은색) 손실이 줄어들지 않으면 학습률을 감소시킨다.

5. 1사이클 스케줄링
   1사이클은 훈련 절반동안 초기 지정 에타를 선형적으로 n1까지 증가시킨다. 나머지 절반은 증가된 n1을 n0으로 선형적으로 되돌린다. 나머지 몇 번의 에폭동안은 선형적으로 줄인다.

• n1은 직접 지정
• n0은 10배 작은 값 선택