[핸즈온 머신러닝] 11. 심층 신경망 - 규제

박경민·2023년 5월 23일

[Hands-On Machine Learning]

목록 보기

18/23

규제를 사용해 과대적합 피하기

심층 신경망은 수만, 수백만 개의 파라미터를 가지고 있으므로 네트워크의 자유도가 매우 높다. 그러나 이런 자유도를 가지면 역시나 오버피팅의 위험이 있으므로 규제가 필요하다.

L1, L2 규제
드롭 아웃
맥스 노름 규제를 알아보자!

1. L1, L2 규제

L1 규제의 경우 많은 가중치를 0으로, L2 규제의 경우 0은 아니지만 실수값으로 가깝게 가중치를 제한한다고 하였다.

다음은 규제 강도 0.01 을 사용하여 L2 규제를 적용하는 코드이다.

layer = keras.layers.Dense(100, activation="elu",
                           kernel_initializer="he_normal",
                           kernel_regularizer=keras.regularizers.l2(0.01))

2. 드롭아웃

심층 신경망에서 인기 있는 규제 방법 중 하나인 드롭아웃drop out 에 대해서도 살펴보자.

드롭아웃은 해당 훈련 스텝에서 임시적으로 사용하지 않을 각 뉴런을 정하는 것이다. 하이퍼파라미터 p가 드롭아웃비율인데, 전체 뉴런 중 p 의 비율만큼 순전파/ 역전파에 참여시키지 않는 것을 말한다.

보통 0.1 - 0.5 로 설정하는 것이 좋은 성능을 보장하며
순환신경망은 0.2-0.3 / 합성곱신경망은 0.4-0.5 사이를 지정한다.
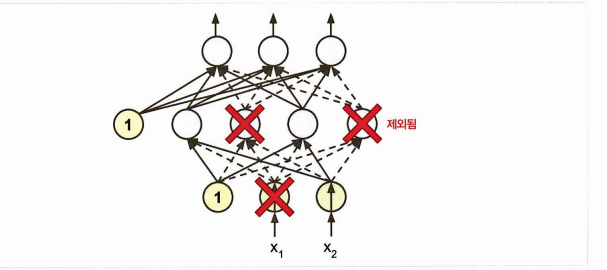
이렇게 드롭아웃 하는 것이 왜 규제가 될까? 일반화 성능을 높이기 때문이다. 왜? 튀는 값을 내는 뉴런 몇 개를 제거할 수 있기 때문이다. (확률적으로)
또한 드롭아웃은 매 훈련 스텝에서 다른 네트워크를 만들어낸다. (n개의 뉴런이라면 경우의 수는 2^n) 따라서 각 훈련 스텝에선 다른 네트워크가 훈련하게 될 것이고, 최종 만들어진 신경망은 모든 신경망을 평균한 앙상블과 같은 형태이다.

한 가지 중요한 점은 드롭아웃을 적용한 훈련을 했다면 테스트하기 전 훈련이 끝난 뒤 각 가중치에 보존확률 1-p를 곱해야 한다. 왜? >> 드롭아웃을 적용하여 훈련하면 훈련을 할 때와 달리 테스트할 때 하나의 뉴런이 1-p만큼 더 많은 입력 뉴런과 연결되기 때문이다. 결국은 하나의 뉴런은 가중합(weighted sum)을 이용한 계산을 할 것이므로, 드롭아웃을 적용할 때보다 그만큼의 스케일이 커질텐데, 이를 꼭 보존해야 하는 것이다.

쉽게말해 드롭아웃 p로 일반화된 추세를 파악하고, 다시 원본 뉴런들의 가중치의 스케일 보존을 위해 보존 확률 1-p 를 곱해줘야 한다는 것!

keras.layers.Dropout 으로 구현된 모든 츠에서 드롭아웃 0.2 를 유지하는 코드를 보자.

model = keras.models.Sequential([
    keras.layers.Flatten(input_shape=[28, 28]),
    keras.layers.Dropout(rate=0.2),
    keras.layers.Dense(300, activation="elu", kernel_initializer="he_normal"),
    keras.layers.Dropout(rate=0.2),
    keras.layers.Dense(100, activation="elu", kernel_initializer="he_normal"),
    keras.layers.Dropout(rate=0.2),
    keras.layers.Dense(10, activation="softmax")
])

3. 몬테 카를로 드롭아웃

2016년에 발표된 논문은 다음 내용을 포함한다

드롭 아웃 네트워크와 근사 베이즈 추론 사이 관련성
드롭 아웃 모델을 재훈련하지 않고 성능을 향상시킬 수 있는 몬테 카를로 드롭아웃 기법(MC dropout)

y_probas = np.stack([model(X_test_scaled, training=True)
                     for sample in range(100)])
y_proba = y_probas.mean(axis=0)

# 드롭아웃을 적용하지 않은 예측 
np.round(model.predict(X_test_scaled[:1]), 2)

# 드롭아웃 활성화한 예측 
np.round(y_probas[:, :1], 2)
# 드롭아웃 활성화, 평균 예측 
np.round(y_probas[:1], 2)

model(X)에서 training = True 를 지정하면 Dropout 층을 활성화시킬 수 있다. 반복문을 돌면서 모델을 호출할 때마다 각 클래스를 담고 있는 샘플이 행으로 들어간다. 한 번 돌면 10,000 의 샘플, 10개의 클래스가 들어가고 100번 돌아서 최종적으로
y_probas 는 [100, 10000, 10] 크기의 행렬이 된다. 이를 평균하여 다시 10000, 10 크기로 만들어준 것이 y_proba

드롭아웃을 활성화하고, 평균을 다룬 예측을 보면 실제 하나의 행에 대해 99% 확신하던 것을 62%만 활성화하는데 훨씬 납득할만한 주장이다. 이렇게 MC 드롭아웃을 적용한 모델을 사용하면 그렇지 않은 모델보다 정확도도 향상된 것을 확인할 수 있었다.

정리하면 MC 드롭아웃은 훈련하는 동안은 일반적인 드롭아웃처럼 규제, 추정에 있어서 추가적으로 불확실한 추정(확률을 낮춰 정확성을 높이는)을 제공하는 기술이다.

4. Max-Norm 규제

또다른 규제 방법인 Max-Norm 에 대해 알아보자.
각각의 가중치가 $||w||_2 <=r$ 이 되도록 훈련한다.

r: 맥스 노름 하이퍼파라미터
L2 노름

전체 손실함수에 항을 추가하는 대신 훈련 스텝이 끝나면 L2 노름을 계산하고, 필요하다면 w의 스케일을 조정하는 방식이다.

$w = w* r / ||w||_2$

r를 작게하면 스케일이 많이 줄어들어 규제가 늘어난다고 보면 된다. 이제 코드에서의 구현을 보자.

layer = keras.layers.Dense(100, activation="selu", kernel_initializer="lecun_normal",
                           kernel_constraint=keras.constraints.max_norm(1.))