CNN
- 합성곱 신경망은 대뇌의 시각피질 연구에서 시작되었고, 1980년대 이미지 인식 분야에서 사용
- 메인은 시각 + 음성 인식, 자연어처리까지!
CNN의 배경과 구성요소, 구현방법과 뛰어난 성능을 보이는 CNN구조 몇 개를 알아보자.
Ojbect detection 과 Semantic segmentation 에 대한 작업에 대해서도 다룰 것이다!
14.1 시각 피질 구조
원숭이 대상 실험에서,
- 시각 피질 안 많은 뉴런이 국부 수용장을 가진다는 것을 보임
- 수용장들을 합치면 전체 시야 커버, 어떤 뉴런은 수평선 이미지에, 어떤 뉴런은 각도와 선분에 반응
- 저수준 뉴런을 출력을 받으면 고수준 뉴런의 출력이 또다시 생성, 큰 수용장으로 연결
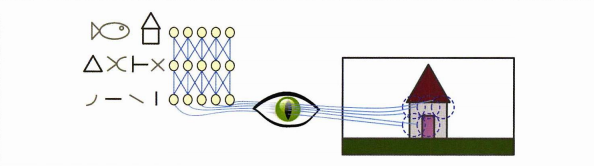
처음엔 수평,수직,대각선으로 시작, 고수준으로 올라가며 정교화된 패턴으로 반응한다는 것!
이러한 시각피질 연구는 현재 합성곱신경망(convolutional Neural Network)라 부르는 것으로 발전되었다. 1998년 LeNet-5 구조를 소개한 논문에서 기존 완전연결층, 시그모이드 활성화 함수 이외에도 합성곱 층, 풀링층 구성요소가 소개되었다. 본격적으로 알아보자!
14.2 합성곱 층
CNN의 가장 중요한 요소는 convolutional layer 라 불리는 합성곱 층이다.
- 첫번째 합성곱 층 뉴런은 해당 합성곱층 뉴런의 수용장 안의 픽셀(입력 이미지의 픽셀 중)에 연결된다.
- 두 두번째 합성곱 층 뉴런은 첫 층의 사각영역에 위치한 뉴런에 연결된다.
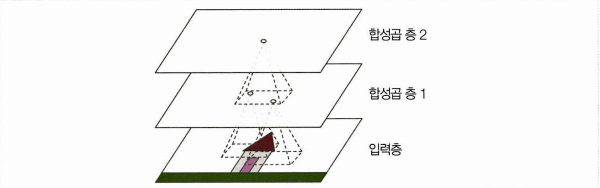
- 연쇄적으로 어떤 층의 (i,j) 좌표의 한 뉴런은 이전 층의 i에서 i+f-1행, j에서 j+f-1 열에 있는 뉴런의 출력에 연결된다. (f에 따라 이전 층의 제로패딩 추가)
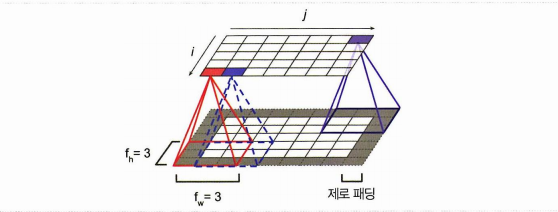
스트라이드란 위의 그림에서 어떤 층이 이전층과 연결되었을 때 매핑되는 이전 층 픽셀 사이의 간격을 말한다.(커널이 움직이며 스캔하는 보폭이다)
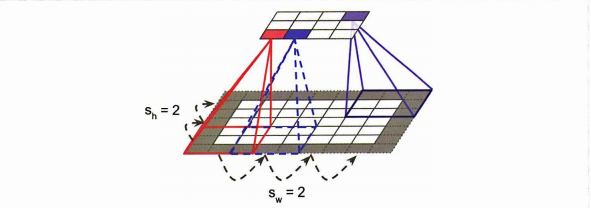
- 위 사진에선 첫 수용장과 다음 수용장이 간격 2를 두고 연결되었으니, 스트라이드=2라 할 수 있다.
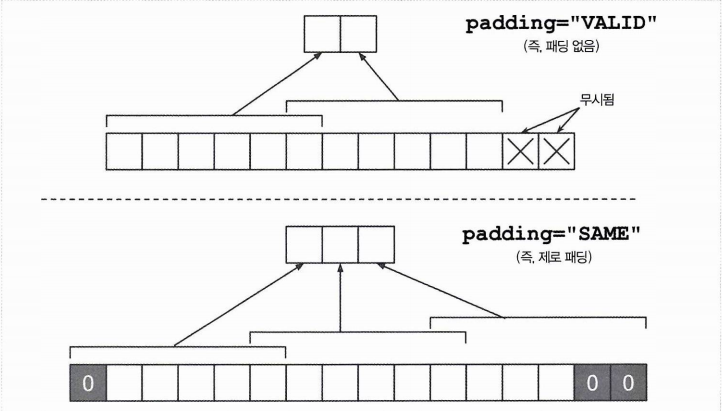
패딩이란 커널로 스캔하는 과정에서 스캔, 보폭만큼 이동, 스캔이 반복되고 남은 픽셀을 무시할까를 결정하는 여부이다. padding = 'same'은 0인 픽셀을 추가하는 제로패딩 사용, padding = 'valid' 는 패딩 없음을 뜻한다.
1. 필터
CNN에서 뉴런의 가중치 = 커널이 가진다.
예컨대 커널 2X2 라 하면, 2X2 짜리 도장을 온 사진에 찍는 것과 같다!
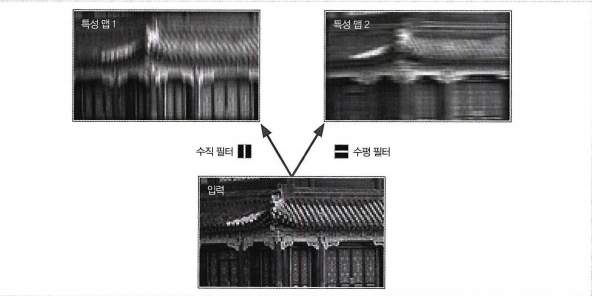
왼쪽은 흰 수직선이 잇는 검은 사각형이다.(가중치=하나의 수용장에 가운데 열이 1로 채워짐), 오른쪽은 흰 수평선이 있는 검은 사각형이다.(하나의 수용장에 가운데 행이 1로 채워짐)
이렇게 입력에 필터(=커널)이 적용된 각각의 결과를 특성맵이라 한다. (합성곱 층은 자동으로 가장 유용한 필터를 찾고 맵을 반환하며 상위 층이 이들을 결합하여 복잡한 패턴을 학습하는 것)
정리하자면, 합성 곱 층 = 하나의 맵은 작은 커널을 입력에 도장처럼 찍어서 만듦 = 커널에 따라 맵의 결과가 달라짐.
2. 여러 가지 특성 맵 쌓기
- 하나의 특성 맵은 같은 가중치와 편향을 가지며, 특성 맵끼리는 다름. (다른 가중치를 가진 커널로 각각 특성 맵을 만든다는 말!)
- 하나의 합성 곱 층 = 특성 맵 여러 개가 쌓인 것 = 여러 특성을 감지
- 특수하게 입력 층은 컬러 채널마다의 서브 층으로 구성되기도 (RGB)
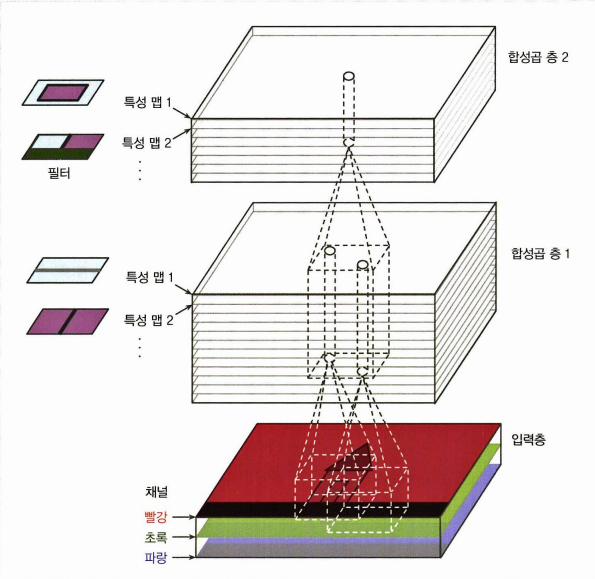
합성곱 층에 있는 뉴런의 출력을 계산하는 식을 보자. 위 이미지를 아래의 식으로 나타낸 것이다.
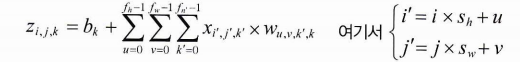
- 구하는 z는 k특성 맵에서 i,j 뉴런의 출력이다
- s는 수직, 수평 스트라이드(수용장 사이 거리)이고 f_n은 이전 층의 특성 맵의 수, f_w, f_h 는 각각 수용장의 너비와 높이이다. (맵만큼 쌓고, 너비가고, 높이 가는 식으로 계산!)
- l-1 층의 k'특성 맵의 i', j'위치에 있는 뉴런의 출력 x에 k와 k' 특성 맵을 잇는 가중치 w를 곱한 값을 사용한다
- b는 l 레이어의 k 특성 맵의 편향이다.
3. 텐서플로 구현
- 가중치 []
- 편향 []
import numpy as np
from sklearn.datasets import load_sample_image
# 샘플 이미지를 로드합니다.
china = load_sample_image("china.jpg") / 255
flower = load_sample_image("flower.jpg") / 255
images = np.array([china, flower])
batch_size, height, width, channels = images.shape
# 2개의 필터를 만듭니다.
filters = np.zeros(shape=(7, 7, channels, 2), dtype=np.float32)
filters[:, 3, :, 0] = 1 # 수직선 (너비 3에만 일정하게 1을 채우니 수직선)
filters[3, :, :, 1] = 1 # 수평선 (높이 3에만 일정하게 1을 채우니 수평선)
outputs = tf.nn.conv2d(images, filters, strides=1, padding="SAME")
plt.imshow(outputs[0, :, :, 1], cmap="gray") # 첫 번째 이미지의 두 번째 특성맵을 그립니다.
plt.axis("off")
plt.show()- 컬러의 픽셀 강도는 0-255 중 하나로 표현되므로 이미지를 로드 한 후 /255 하여 0-1 사이 실수로 바꿔준다
- 필터를 만든다, 현재 만들 필터는 7X7 (흰 수직선 / 흰 수평선 필터이다)
- 이미지에 필터를 적용한다,
tf.nn.conv2d()를 사용한다. 스트라이드 1과 제로패딩(SAME, 사용하지 않으려면 VALID로 지정)을 사용했다.
사실 실제 CNN에서 훈련 가능한 변수로 필터를 정의하므로 코드가 훨씬 간단해진다! 아래의 코드를 사용하자.
conv_same = keras.layers.Conv2D(filters=32, kernel_size=3, strides=1, padding="SAME", activation = 'relu')4. 메모리 요구사항?
CNN은 합성곱 층이 많은 양의 RAM 을 필요로 하므로 주의하자.
- 이런 점을 고려하여 미니배치 크기를 줄여볼 수 있다.
14.3 풀링 층
풀링층 또한 층의 일종으로 계산량 / 메모리 사용량 / 파라미터 수를 줄이기 위한 목적을 가진다. 이를 위해 풀링층에선 입력이미지의 부표본을 만든다. 말이 어렵지만 특정 크기와 스트라이드에 대하여 평균 또는 최댓값을 취하여 사진을 줄이겠다는 것이다.
합성곱 층과 마찬가지로 풀링층에서는 이전 층의 수용장이 하나의 뉴런과 연결되며,
- 크기
- 스트라이드
- 패딩 유형을 지정해주어야 한다.
- 그러나 풀링 뉴런은 가중치가 없다! (단순히 평균을 내거나 최대값을 취한다.)
아래의 예를 보자.
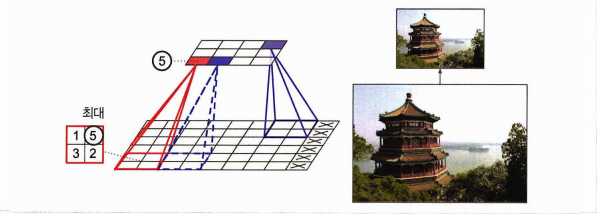
해당 풀링층은
- 최대값을 취하는 최대 풀링층이며
- 2 X 2 풀링 커널
- 스트라이드 2
- 패딩은 없다.
이렇게 풀링을 사용하면 위에서 소개한 장점을 취하는 것에 더하여 일정 수준의 불변성, invariance 를 보여준다. 이동 불변성이란 입력으로 들어온 이미지가 겉보기엔 다르지만 결국은 단순히 축에 대해 이동한 사진일 경우 풀링층을 통해 불변성을 유지한다는 것이다.
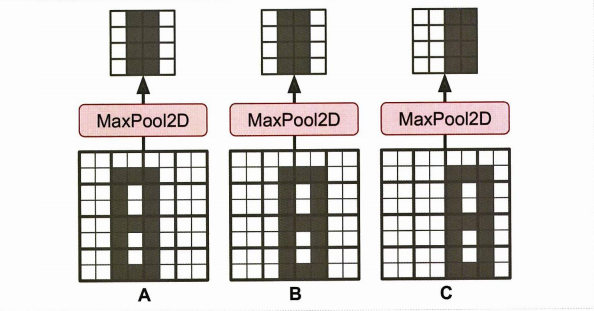
이동 불변성의 반대는 등변성equivariance가 필요한 상황이며 대표적으로 Semantic Segmentation 에선 등변성이 필요하다.
- 풀링 층 구현
풀링층을 구현하는 것은 다음과 같으며 보통 어떤 패딩도 하지 않는다. 다음은 2 X 2 커널을 이용해 최대 풀링층을 만드는 코드이다.
max_pool = keras.layers.MaxPool2D(pool_size=2) (평균 풀링층은 MaxPool2D 의 자리에 AvgPool2D를 사용하자.)
현재까지는 특정 공간(2X2와 같은) 차원에 대해 최대, 평균 풀링을 사용했지만 깊이 차원으로 풀링을 진행할 수 있다. 일단 같은 사진이 회전된 여러 가지 필터를 준비한다. 이에 대해 깊이 방향 최대 풀링층을 적용하면, 회전에 상관없이 동일한 출력을 만드는 것!
추가로 최대, 평균 풀링층 이외에도 전역 평균 풀링 층global average pooling layer을 사용할 수 있을 것이다. 이는 하나의 특성 맵이 주어지면 여러 값이 아닌 단 하나의 숫자를 출력하는 층이다. 보통 출력층에서 유용하다!
global_avg_pool = keras.layer.GlobalAvgPool2D()14.4 CNN 구조
합성곱 층, 풀링층, 완전 연결층을 배웠으니 이를 조합하면 CNN층이 되는 것을 이해할 수 있을 것이다. CNN의 전형적 구조는 다음과 같다.
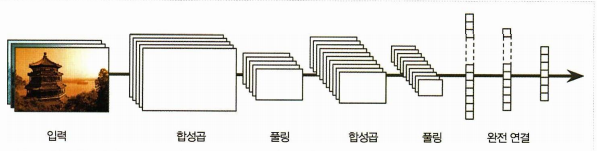
- 합성곱과 풀링 층을 교차
- 네트워크를 통과하며 이미지는 점점 작아짐
- 더 많은 특성 맵을 가짐
- 맨 위에는 완전 연결 층(에 ReLU 등을 더한) feedforward nerual network 가 추가 되고, 마지막 층에서 예측을 출력한다.
간단한 CNN 코드를 보자.
from functools import partial
DefaultConv2D = partial(keras.layers.Conv2D,
kernel_size=3, activation='relu', padding="SAME")
model = keras.models.Sequential([
DefaultConv2D(filters=64, kernel_size=7, input_shape=[28, 28, 1]),
keras.layers.MaxPooling2D(pool_size=2),
DefaultConv2D(filters=128),
DefaultConv2D(filters=128),
keras.layers.MaxPooling2D(pool_size=2),
DefaultConv2D(filters=256),
DefaultConv2D(filters=256),
keras.layers.MaxPooling2D(pool_size=2),
keras.layers.Flatten(),
keras.layers.Dense(units=128, activation='relu'),
keras.layers.Dropout(0.5),
keras.layers.Dense(units=64, activation='relu'),
keras.layers.Dropout(0.5),
keras.layers.Dense(units=10, activation='softmax'),
])- 입력은 28X28 픽셀크기의 하나의 컬러채널이므로 다음과 같이 주고, 보통 입력층의 필터는 필터 수를 작게(64)하고 큰 필터(7X7)를 사용한다
- 커널 2 X 2 인 풀링층을 사용하면 크기를 절반으로 줄일 수 있다.
- 합성곱 층 + 최대 풀링 층을 2번 반복한다
- 출력층으로 올라갈 수록 필터 개수가 증가, 고수준 특성을 만드는 과정이다.
- 필터 개수는 2배 단위로 증가하지만 동시에 풀링 층이 공간 방향 차원을 줄이므로 계산 비용을 크게 늘리지 않으면서 특성 맵 개수를 늘린다
- 두 개의 은닉 층, 하나의 출력층 완전 연결 네트워크를 구성한다. 이를 위해 입력을 일렬로 펼친다.
이제 이러한 기본 구조에서 파생된 변종을 보자. 고전 구조 LeNet-5와, ILSVRC 이미지넷 대회에서 우승한 세 가지 모델(AlexNet, GoogleNet, ResNet)을 보자.
1. LeNet-5
-
1988, 얀 르쿤, MNIST 데이터에 널리 사용
-
층의 구조를 보자.
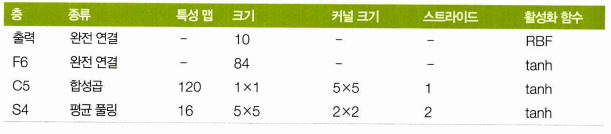
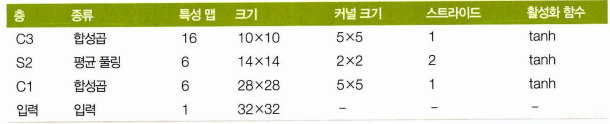
-
MNIST 기본이미지 28 X 28 에 제로 패딩하여 32 X 32 가 되고, 정규화하였다.
-
최근에는 평균 폴링에 학습되는 계수, 편향이 없지만 여기서는 각 뉴런이 입력의 평균을 계산, 계숫값을 곱하고 편향을 더한 것에 활성화 함수를 적용했다.
-
C3의 뉴런은 맵 전체가 아닌 3,4개 맵의 뉴런에만 연결된다.
-
출력은 이미지가 얼마나 특정 숫자 클래스에 속하는지 측정하고, 일반적인 가중치 벡터와의 곱셈 대신 입력 벡터, 가중치 벡터 사이 유클리드 거리를 출력한다.
2. AlexNet
-
2012년 이미지넷 대회에서 2위 26% 에러율과 큰 차이인 17% 에러율을 기록한 CNN
-
합성곱 층 위에 폴링 층이 아닌 합성곱 층끼리 쌓은 구조가 특징
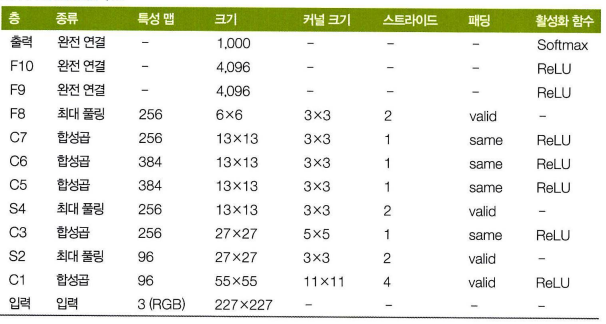
-
합성곱끼리 그대로 쌓았을 때의 문제는 과대적합 발생 가능성이며, 이를 줄이기 위해 두 가지 규제를 사용한다
- F9, F10 드롭아웃 50% 비율을 적용
- 훈련 이미지를 간격에 따라 이동, 뒤집고, 조명을 바꾸는 데이터 증식 수행 (예컨대 조명 조건에 민감하지 않은 모델을 만들기 위해 여러 명암을 가진 이미지를 생성할 수 있다.)
- C1, C3 렐루 함수의 적용 다음에 LRN(local response normalization) 이라 부르는 경쟁적인 정규화 단계를 사용했다. 의도는 가장 강하게 활성화된 뉴런이 다른 특성 맵의 같은 위치 뉴런을 억제하는 것이다.

- 는 특성 맵에 위치한 뉴런의 정규화된 출력은
- 는 렐루를지나고 정규화는 거치기 전의 뉴런 활성화 값에
- 로 정해진 깊이 반경만큼의 값들을 연산한 값을 곱한 것이다.
- 연산을 거치면 특성맵의 해당 값이 상대적으로 크면 다른 특성맵의 값들을 억제할 수 있다.
3. GoogLeNet
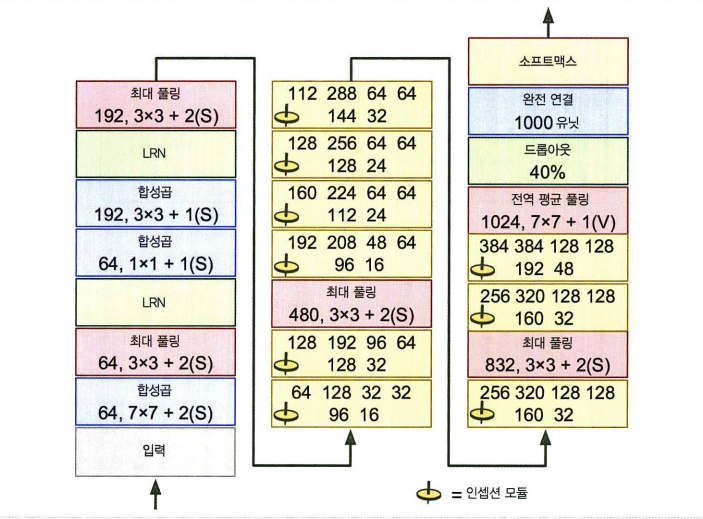
- 구글 리서치가 개발한 GooGleNet 구조
- 인셉션 모듈이라는 서브 네트워크로 이전보다 훨씬 효과적으로 파라미터를 사용. (아래는 인셉션 모듈만의 사진이다.)
- AlexNet 보다 10배나 적은 파라미터
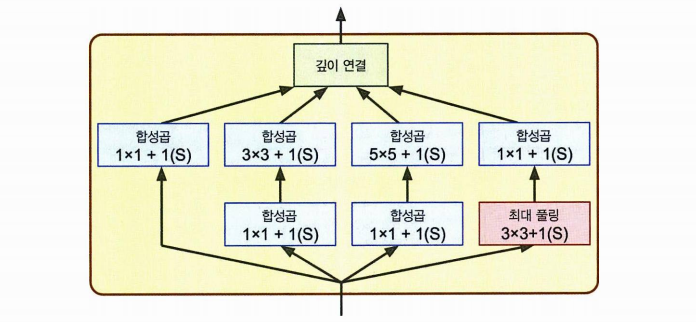
- 첫 층에서는 입력신호 복사(1X1 커널), 네 개의 다른 층에 주입, ReLU 활성화 함수 사용
- 두 번째 층에서는 다른 커널 크기 (1, 3, 5) 를 사용하여 다른 크기의 패턴을 잡음. (그러나 스트라이드1 + 패딩이므로 출력과 입력의 크기 유지)
- 맵의 크기가 모두 같으므로 깊이 연결 층에서 깊이 방향으로 4개맵 연결 가능.
인셉션 모듈에서 1X1 커널을 사용한 이유는 무엇일까?
- 깊이 차원을 따라 패턴을 잡기에 용이하기 때문이다
- 입력 차원보다 적은 특성 맵을 출력하므로 차원을 줄이는 의미인 병목층의 역할을 담당한다 >> 왜일까? 이때는 특성 맵의 크기가 아닌 개수를 의미한다. 파라미터 수를 줄이고 일반화 향상!
- 합성곱 층의 쌍 [1X1, 3X3] , [1X1, 5X5] 가 복잡한 패턴을 감지하는 강력한 합성곱 층처럼 작동한다.
4. VGGNet
- 2014 ILSVRC 대회 2등
- 단순하고 고전적인 구조: 2개의 합성곱 뒤에 풀링, 다시 2개의 합성곱과 풀링, 마지막 밀집 네트워크는 2개의 은닉층과 출력층
- VGGNet 은 3X3 필터만 사용
5. ResNet
- 트렌드는 더 적은 파라미터로 더 깊은 네트워크로 모델을 구성하는 것이었다
- 깊은 네트워크를 훈련시킬 핵심 요소는 스킵 연결 이다.
- 스킵 연결 해당 층에 주입되는 신호가 상위 층의 출력에도 더해진다!
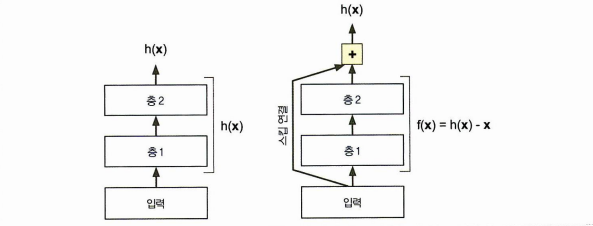
사진에서 층1, 2를 통틀어 목적함수(모델링의 대상)라 하면, 여기서 잔차 학습이란 오른쪽과 같이 로 구성하는 것이다. (=스킵 연결을 추가한다고 한다.)
스킵 연결로 시작하여 스킵 연결로 끝나는 한 단위를 잔차 유닛이라 볼 수 있으며(residual unit), 이러한 연결이 쌓이면 심층 잔차 네트워크가 된다.
왜 이런 연결을 추가할까?
- 이렇게 스킵 연결을 추가하면 훈련 초기에 가중치가 0이어도 적어도 입력과 같은 값을 출력한다. (훈련 속도가 빨라진다.)
- 학습되지 않은 층이나 방해하는 층을 넘어 훈련이 가능하다.
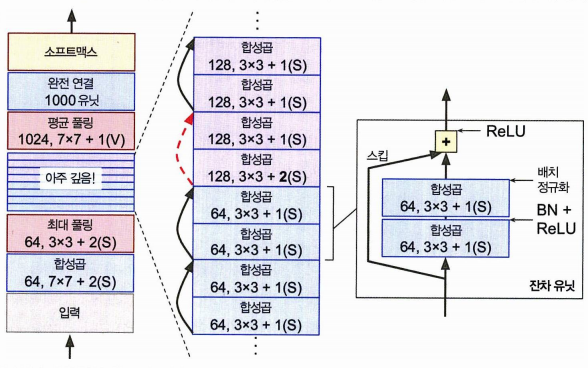
중간에 깊은 잔차 유닛을 쌓은 것 외에 나머지는 GoogleNet 과 똑같다.
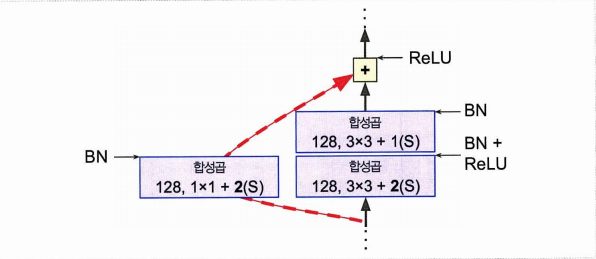
6. Xception
-
GoogleNet + ResNet 이지만 인셉션 모듈을 깊이별 분리 합성곱 층(분리 합성곱) 이라는 층으로 대체.
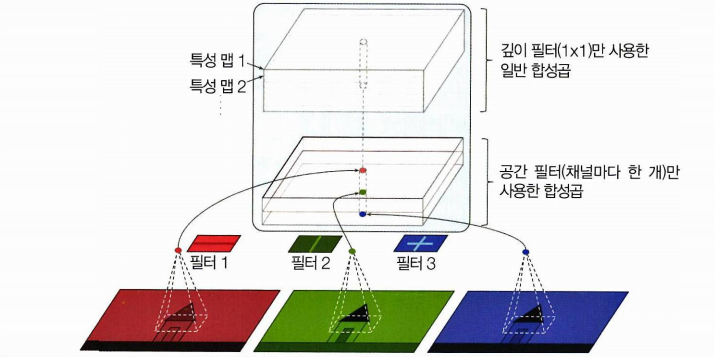
-
일반적인 합성곱 층이 공간상 패턴(타원) / 채널 사이의 패턴(입+코+눈 = 얼굴)을 동시에 잡기 위해 필터를 사용하나,
-
분리 합성곱 층은 공간과 채널 사이 패턴을 분리하여 모델링한다고 가정
따라서
- 첫번째 부분은 하나의 공간 필터를 각 입력 특성 맵에 적용
- 두번째 부분에서는 채널 사이 패턴만 조사