[핸즈온 머신러닝] 4. 모델 훈련 (2)

지난 포스팅에 이은 모델 훈련 (2) 이다.

4.4 학습 곡선

1차, 2차, 300차 선형과 다항회귀를 보자.

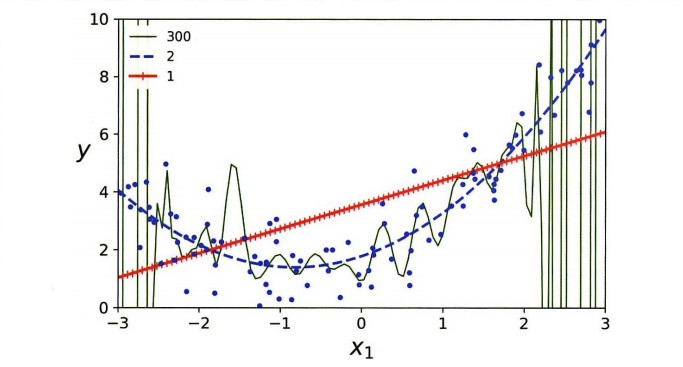
그래프를 보면 1차는 과소적합 / 300차는 과대적합 / 2차가 적당한 것을 알 수 있다. 그러나 이를 객관적으로 어떻게 말할 것인가? 2차,3차,4차 중에는 어떤 모델을 결정할 것인가? 다음은 과소/과대적합을 판단해볼 수 있는 방법이다.

✅ 교차검증 사용하기 : 훈련 데이터에서 성능이 좋지만 교차검증 점수가 나쁘다면 과대적합 / 훈련 데이터에서도, 교차 검증 점수도 낮으면 과소적합

✅ 학습 곡선 살펴보기 : 훈련 세트 크기에 따른 훈련 세트와 검증 세트의 모델 성능을 보여준다. 과소적합, 과대적합에 따른 학습곡선이 다르므로 이를 살펴보자.

과소적합 모델의 학습곡선🔽

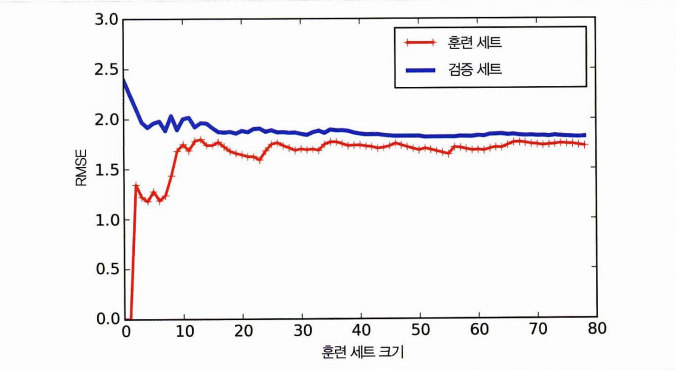
• 과소적합의 경우 훈련 세트에 대한 성능은 1개-2개일 때 잘 작동
• 훈련세트가 늘어나면 훈련세트 성능은 계속 상승 > 평편해지는 구간
• 검증세트 성능의 경우 1개-2개일 때 오차 큼
• 데이터가 늘어남에 따라 감소 > 감소가 완만해짐 (데이터를 완전히 모델링할 수 없다는 것!)

따라서 두 곡선이 수평한 구간을 만들었으며 / 오차가 근접했으면 과소적합이라 판단하자.

과대적합 모델의 학습곡선🔽

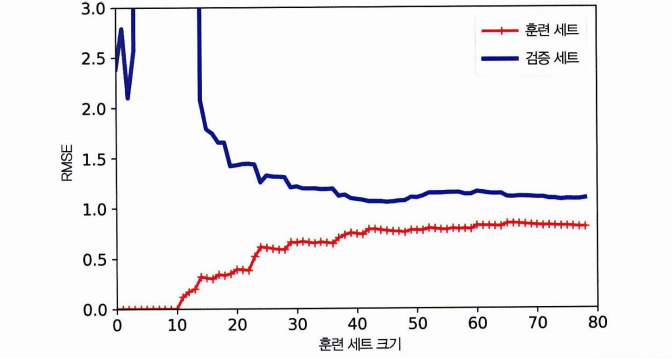
• 비슷해보이지만 훈련 데이터의 오차가 과소적합 때보다 낮음
• 두 곡선 사이 공간이 있음. > 훈련 데이터에서 더 낫고, 검증 데이터에서 성능은 차이가 있다. > 과대적합이다.
• 훈련 세트를 키울수록 두 곡선이 가까워짐. (이상적!)

💡편항-분산 트레이드오프!
일반화 오차는 다음 세가지 오차의 합으로 표현할 수 있다.

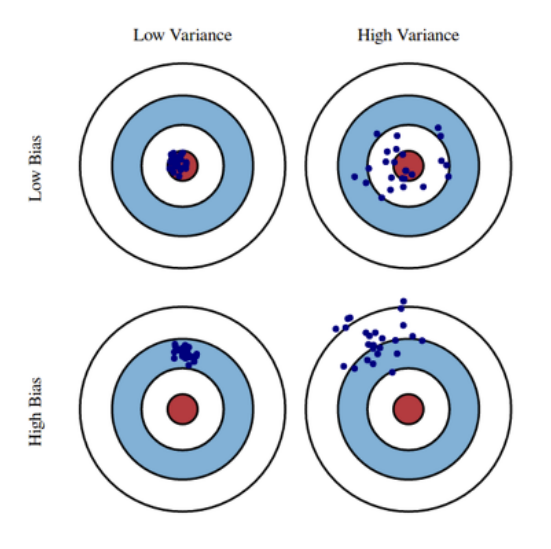
• 편향
  편향이 크다는 것은 실제 값(가운데 빨간색)에서 멀리 벗어난 예측을 한다는 것이다. 당연히 목표는 빨간색 점으로 다가가는 것이기에 편향을 작게하면, 분산이 늘어난다.

• 분산
  분산이 크다는 것은 예측의 점들이 서로 민감하게 반응한다는 것이며, 자유도가 높다 = 과대적합의 가능성이 있다.

• 줄일 수 없는 오차
  잡음을 이야기한다. 유일한 방법은 잡음을 제거하는 것 뿐!

간단히 정리하여 점에 가까이 다가가기 위해 편향을 작게하면 점들 사이의 거리가 멀어지고(과대적합), 이를 가까이하여 분산을 줄이면 실제 값에서 멀리 떨어진다는 것!(과소적합)

4.5 규제가 있는 선형 모델

규제를 한다는 것은 과대적합을 막는다는 말이다.

• 규제 = 과대적합 억제 = 모델 제한 = 자유도 줄임!
• 다항 회귀 모델에서는 다항식의 차수를 감소시킴으로써
• 선형 회귀 모델에서는 모델의 가중치를 제한함으로써 규체

지금부터 가중치를 제한하는 방법을 보자!

✅ 4.5.1 릿지 회귀

릿지회귀는 비용함수에 규제항 알파 X 세타 제곱의 합를 추가한다.

앞서 선형 회귀 모델에서 과대적합이 일어나는 이유는 각 가중치가 커져서라고 했다. 따라서 비용함수에 가중치 제곱을 추가하면, 이 가중치 제곱을 줄이기 위해서 노력할 것을 의도하는 게 릿지 회귀이다.

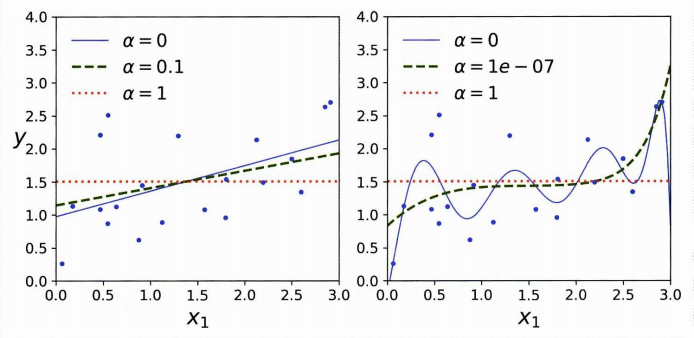
이때 알파는 모델을 얼마다 많이 규제할 지 조절하는 것이다. 알파 = 0이면 규제하지 않는 것이고, 알파가 매우 크면 당연히 이를 줄이기 위해 업데이트 하므로 모든 가중치가 0에 가까워진다. (모델은 수평선에 가까워진다.)

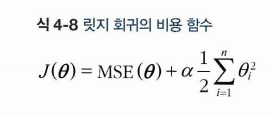
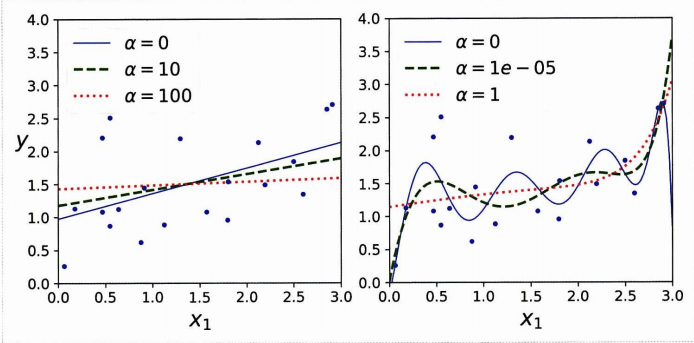
알파의 값에 따른 선형 회귀, 다항회귀의 그래프를 보자.

다음은 세타 = 정규방정식의 해를 구하는 식이다.

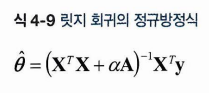
✅ 4.5.2 라쏘 회귀

라쏘 회귀 역시 비용함수에 세타를 더하는 식으로 규제를 하고, 이번에는 알파 X 절댓값 세타의 합을 비용함수에 더해준다.

라쏘 회귀는 절댓값을 사용하므로 덜 중요한 특성의 가중치를 0에 가깝게 하기보다 아예 제거해버린다.= 특성 선택 = 희소모델!

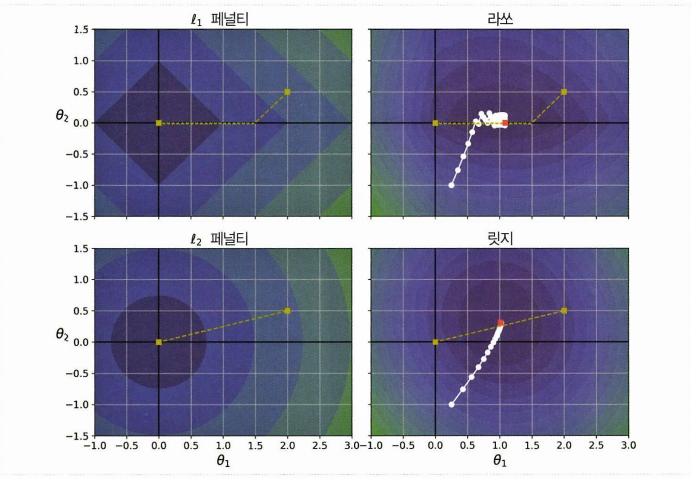
이 사진을 보면 편하다. 파라미터가 두 개만 있다고 가정하고, 등고선은 손실함수를 나타낸다고 하자.

• 라쏘 회귀의 경우 축에 가까워지면 세타2가 0에 가까워지고 / 전역 최적점(빨간 삼각형)에 도달한다.

릿지회귀의 경우 전역 최적점에 가까워질수록 기울기가 작아진다 / 느려진 경사하강, 수렴에 도움 / 알파를 증가시킬수록 최적에 가까워지고 / 0이 되지 않는다.

✅ 4.5.3 엘라스틱넷

둘의 절충안이다! 혼합 비율 r을 사용해 조절한다.

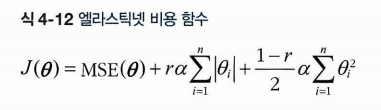
• 기본은 릿지
• 특성이 적으면 라쏘, 엘라스틱 (불필요를 0으로)
• 특성 수가 훈련 샘플보다 많거나 연관이 강하면 엘라스틱

4.5.4 조기종료

검증에러가 최솟값에 도달하면 훈련을 중지시키는 것을 얼리스타핑이라고 한다. (early stopping)

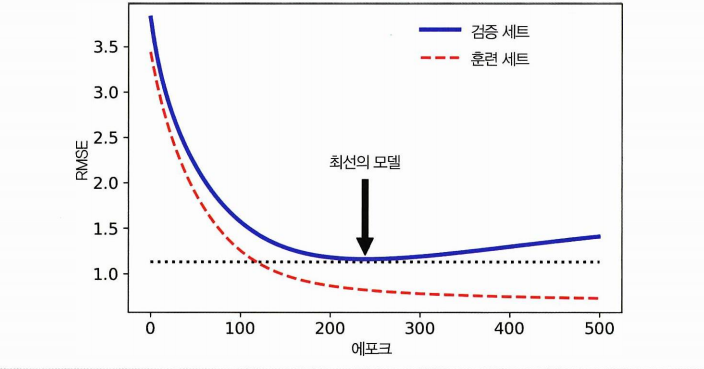
• 에포크가 진행되면 훈련세트, 검증 세트 예측에러가 모두 줄어든다
• 감소하던 검증 에러가 다시 상승 (과대적합!)
• 따라서 검증 에러가 최소에 도달하면 얼리스타핑.

4.6 로지스틱 회귀

로지스틱 회귀는 샘플이 특정 클래스에 속할 확률을 추정하는데 사용.
(ex. 이메일이 스팸일 확률 계산) 추정확률이 50%가 넘으면 모델은 샘플이 해당 클래스에 속한다고 예측하며, (레이블 1인 양성 클래스), 아니면 레이블 0 인 음성 클래스에 속한다고 예측.

4.6.1 확률 추정

선형 회귀 모델과 같이 로지스틱 회귀 모델은 특성 X 가중치들의 합을 계산한다. 계산한 값에 로지스틱 = 시그모이드 함수를 씌우면 식이 완성된다!

• 예측값 p' 로 표시할 수 있다
• 함수 h(x) 로 표시할 수도 있으며
• 시그모이드 함수에 인자로 특성 X 가중치 합을 넣는 것일 수도 있다!

시그모이드 함수는 다음과 같다.

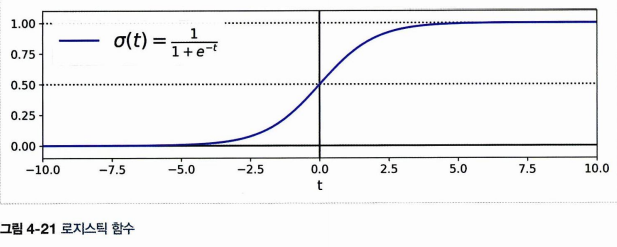
따라서 시그모이드 함수는 t값이 커질수록 1에 가까워지고, t값이 작아질수록 0에 가까워져 인풋이 어떻든 0과 1 사이 값을 출력하게 되며,

• 보통 0.5 이상을 1
• 그 이하를 0이라 본다.

위의 그래프를 다시 잘 보면 t < 0 이면 0.5보다 작고, t>0 이면 0.5보다 커지므로 로지스틱 회귀는 특성 X 가중치 합이 양수일 때 양성, 음수일 때 음성이라고 예측한다 할 수 있다.

4.6.2 훈련과 비용 함수

훈련의 목적은 y = 1 에 관해서는 높은 확률을 추정, y = 0 에 관해서는 낮은 확률을 추정하는 파라미터 세타를 찾는 것이다.

y = 1 이라는 것은 보고있는 하나의 훈련 샘플은 분명 양성이라는 것이다. 그러므로 비용은 예측 p' 가 0에 가까워질수록 커지고, 1에 가까워질수록 작아져야 한다.
마찬가지로 y = 0 일 때는 p'0 가 0에 가까워질수록 작아지고, 1에 가까워질수록 커져야 한다. 로그 그래프가 기억이 잘 안나면 다음을 참고하자.

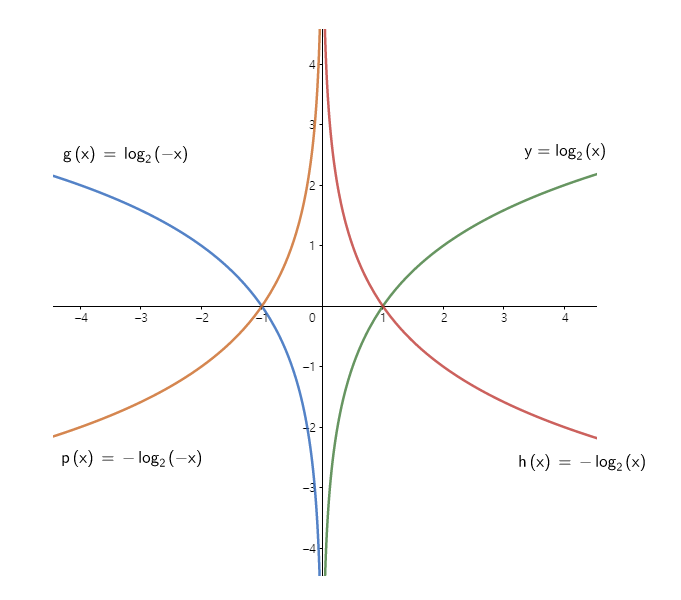
이제 모든 샘플의 비용을 평규난 전체 훈련 세트의 비용함수를 보자.

복잡해보이지만 어려울 것이 없는게, 앞에 각각 곱해진 y 가 스위치 역할을 해주는 것이다. 만약 y = 1이라면 뒤가 꺼지고 앞만 계산하게 되며, y = 0이라면 앞이 꺼지고 뒤만 계산하게 되는 것이다. -는 앞으로 빼주었고 1/m로 평균을 해준 것이다!

이제 다시 세타에 대해 편미분을 해서 최솟값을 갖는 지점을 알아보자.

놀랍게도 위 식을 편미분한 값은 원래 로지스틱 함수에 X를 곱한 값이었다! 좀 더 구체적으로 보면, 위 식은 각 샘플에 대한 예측 오차 * 특성 값 의 평균이다.

4.6.3 결정 경계

꽃잎의 너비를 기반으로 Iris-Virginica 를 감지하는 분류기를 만들어보자.

#데이터셋 로드 
from sklearn import datasets
iris = datasets.load_iris()

# data 중 너비 정보 추출
X = iris["data"][:, 3:]  # 꽃잎 너비
y = (iris["target"] == 2).astype(int)  # Iris virginica이면 1 아니면 0

# 모델 훈련 
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression(solver="lbfgs", random_state=42)
log_reg.fit(X, y)

# 꽃잎 너비 0-3 인 꽃에 대해 추정 확률 
X_new = np.linspace(0, 3, 1000).reshape(-1, 1)
y_proba = log_reg.predict_proba(X_new)

plt.plot(X_new, y_proba[:, 1], "g-", linewidth=2, label="Iris virginica")
plt.plot(X_new, y_proba[:, 0], "b--", linewidth=2, label="Not Iris virginica")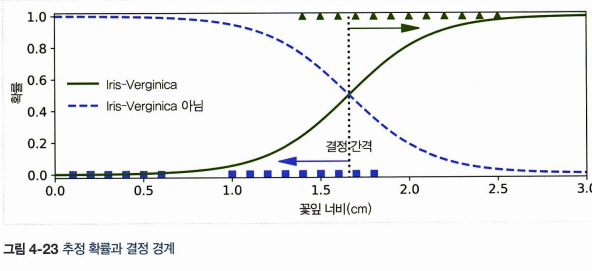

두 극단 사이에서는 분류가 확실하지 않은데 클래스를 예측하력 하면 가장 가능성 높은 클래스를 반환한다. 똑같이 확률이 50%가 되는 1.6cm 근방에서 결정 경게가 만들어진다.

log_reg.predict([[1.7], [1.5]])

4.6.4 소프트맥스 회귀

로지스틱 회귀 모델을 다중 클래스를 지원하도록 일반화한 것을 소프트맥스 회귀(= 다항 로지스틱 회귀) 라 한다.

샘플 x가 인풋으로 주어지고, 샘플 x의 클래스 k에 대한 점수 $s_k(x)$ 를 산출한다. 이 점수에 소프트맥스 함수(= 정규화된 지수함수) 를 적용하면 클래스의 확률을 추정할 수 있다!

$s_k(x)$ 는 다음과 같다.

세타와 x의 곱으로 같지만 이번엔 각 클래스가 가지는 파라미터 벡터이다. 행 기준으로 저장된다!

통과시키는 소프트맥스 함수는 다음과 같다. 인풋은 s(x)이며, 소프트맥스 함수를 통과시켜 얻게 되는 값은 클래스 k에 속할 확률 $p_k$이다. 소프트맥스함수는

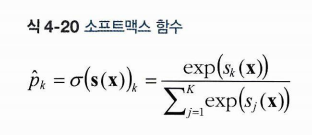
• 분자는 클래스 k에 대한 점수를 인풋으로 지수함수를 적용한 것
• 분모는 모든 지수 함수 결과의 합
• K는 클래스 수
• 따라서 샘플 x > 샘플에 대한 각 클래스의 점수를 담은 벡터 > 샘플이 클래스 k에 속할 확률

🤔 훈련 방법?

타깃 클래스에 대해서는 높은 확률, 타깃이 아닌 다른 클래스에 대해서는 낮은 확률을 반환해야 하므로 크로스 엔트로피 비용함수를 최소화하는 것을 목표로 하자. (크로스 엔트로피 => 추정된 클래스의 확률과 실제 타깃 클래스를 비교!)

• y는 i번째 샘플이 클래스 k에 속할 타깃 확률
• 로지스틱 회귀의 비용함수를 일반화 해놓은 것

이를 세타에 관해 미분한 결과는 다음과 같다.

(샘플i가 k에 속할 확률 - 실제) X i번째 샘플을 더한 값의 평균과 같다!

🤔구현?
실제 구현은 다른 게 아니라 LogisticRegression 을 만들 때 multi_class = 'multinomial' 의 매개변수를 주고, solver = 'lbfgs' 를 주면 된다.

#똑같이 logisticRegression 가져온다. 
from sklearn.linear_model import LogisticRegression

# 이번엔 data 에서 길이와 너비를 가져오도록 하고, y 는 여전이 virginica 를 발견하는 클래스로 한다.
X = iris["data"][:, (2, 3)]  # petal length, petal width
y = (iris["target"] == 2).astype(int)

#모델 만들고, 훈련 
log_reg = LogisticRegression(solver="lbfgs", C=10**10, random_state=42)
log_reg.fit(X, y)

# 품종이 무엇인지 질의 
softmax_reg.predict([[5, 2]])

# 전체 확률 확인
softmax_reg.predict_proba([[5,2]])

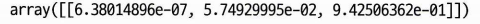
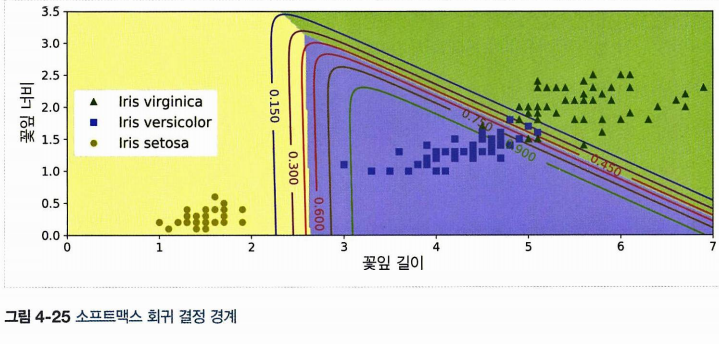
색으로 구분한 결정경계는 다음과 같다. 직선 사이에 있는 숫자는 그만큼의 확률을 뜻한다!