[핸즈온 머신러닝] 8. 차원 축소

차원의 저주란 훈련 샘플 각각이 가진 특성이 너무 많아져 훈련을 느리게 하고, 좋은 솔루션을 찾는 것을 방해하는 것을 말한다. 이런 경우 사용하는 것이 차원 축소이다.

✅ 차원을 축소시키면 일부 정보가 유실되어 속도가 빨라질 수 있지만 성능이 조금 나빠질 수 있다.

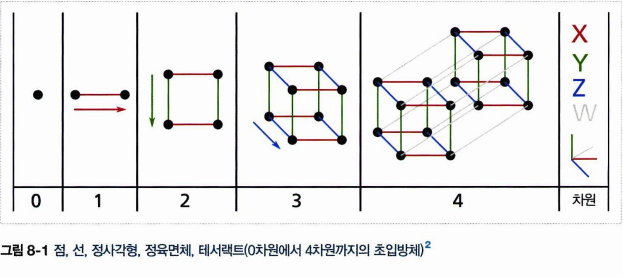
• 차원의 저주
• 고차원 공간에서 발생하는 일
• 차원 축소 접근 방법 (투영, 매니폴드 학습)
• PCA, 커널 PCA, LLE

8.1 차원의 저주

• 단위 면적에서 두 점 선택하면 거리는 평균 0.52가 됨
• 3차원에서 두 점 평균은 0.66
• 1,000,000 차원이된다면 408.25
• 이는 고차원이 많은 공간을 가지고 있기 때문.
• 같은 말로 고차원에 위치한 데이터셋은 서로 멀리 떨어져있음.
• 과대적합 위험이 커짐.
• 밀도가 높아질 때까지 훈련 세트의 크기를 키울 수 있으나 훈련 샘플이 너무 많이 필요.

8.2 차원 축소를 위한 접근 방법

지금 알아볼 것은 차원을 감소시키는 주요 접근법이다. (알고리즘 x)

8.2.1 투영

• 대부분 실전 문제의 경우 훈련 샘플이 모든 차원에 균일하게 퍼져있지 않음

• 고차원 안의 저차원 부분공간에 놓여 있음.
  

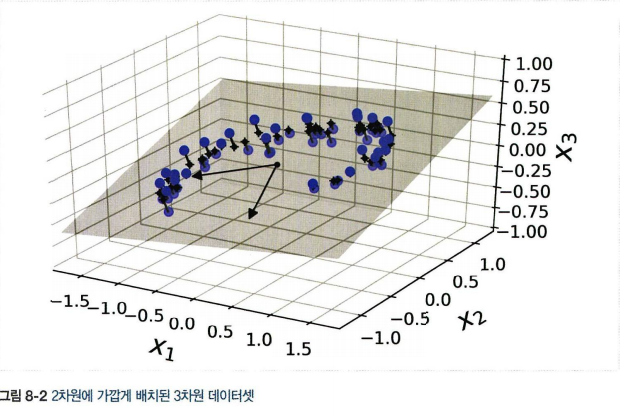
• 특성이 3개라 3차원에 표현되었지만 거의 평면과 같음.

• 이를 수직으로 투영하면 2D 데이터셋을 얻음.

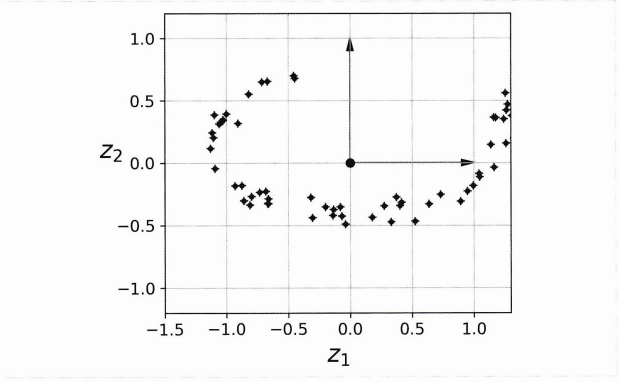
• 이를 투영이라 하는데, 그러나 항상 최선이 아닌 것이 많은 경우에 스위스롤 처럼 부분 공간이 휘어있기도 하다.
  

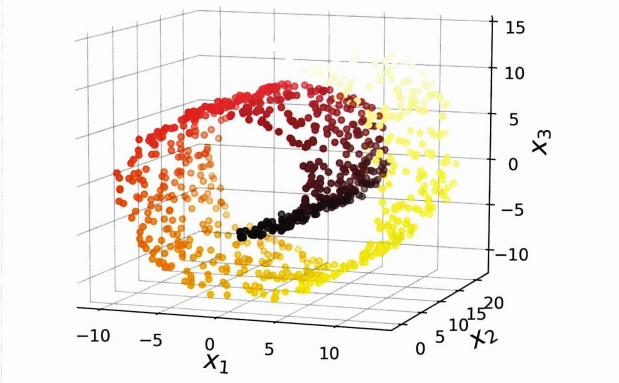
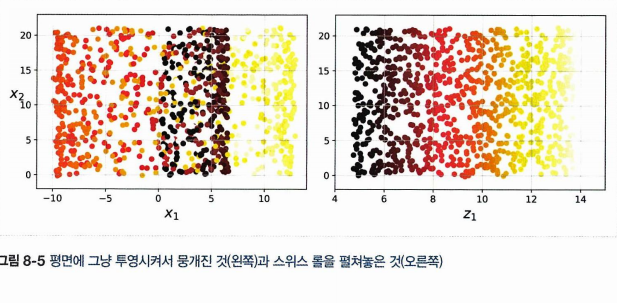
이를 투영하면 층이 서로 뭉개지므로 왼쪽처럼 펴서 얻는 편이 더 의미가 있어보인다.

8.2.2 매니폴드 학습

2D 매니폴드는 고차원 공간에서 휘어지거나 뒤틀린 2D 모양을 말한다. (2D 매니폴드의 한 예가 스위스롤)
= d차원 매니폴드는 d차원 초평면으로 보일 수 있는 n차원 공간의 일부이다. (스위스롤은 d=2, n=3)

따라서 매니폴드 학습이란 훈련 샘플이 놓인 매니폴드를 모델링하는 것이다. (저차원 매니폴드에 가깝게 있다는 매니폴드 가정, 가설에 근거)

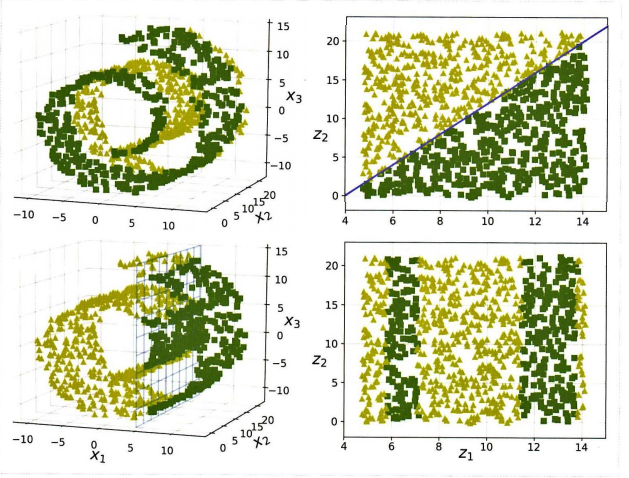
매니폴드는 데이터가 저차원 매니폴드에 표현되면 간단해질 것이라 가정하지만 항상 그렇지는 않다. 사진의 첫 행의 경우 그러하지만, 두 번째 행은 오히려 복잡.

따라서 훈련 세트의 차원을 감소시키면 훈련 속도는 빨라지나, 더 낫거나 간단하다고 보장할 순 없다.

이제 직접 알고리즘을 보자!

8.3 PCA

주성분 분석principal component analysis(PCA) 는 차원 축소 알고리즘 중 가장 인기가 있다. 데이터에 가장 가까운 초평면을 정의하고, 이 평면에 데이터를 투영하는 방식!

8.3.1 분산 보존

그렇다면 올바른 초평면은 어떻게 선택할까?

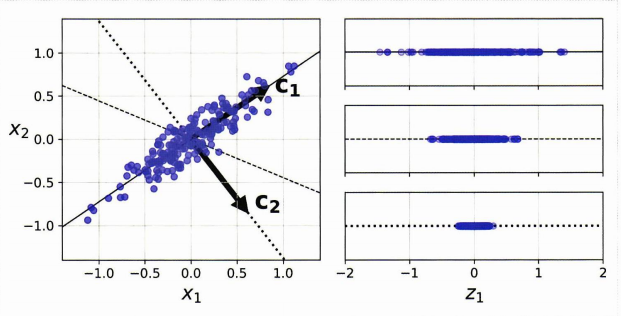
왼쪽의 2차원 데이터셋을 3개의 1차원 초평면에 투영한다고 해보자. 오른쪽이 각 초평면에 대한 투영의 결과이다. 무엇이 가장 잘 나타냈는가? 기준은 분산을 최대로 보존하는 것이며, 이에 따라 실선이 가장 적합, 그 다음 파선, 점선 순으로 보인다.

분산을 최대로 보존하는 것의 다른 말은 원본 데이터셋과 투영된 결과 사이 평균 제곱 거리를 최소화하는 축을 고르는 것이다.

8.3.2 주성분

PCA는 결국 훈련 세트에서 분산이 최대인 축을 찾는다(실선). 그 후, 첫 번째 축에 직교하고 남은 분산을 최대한 보존하는 두 번째 축을 찾는다. (위에선 2차원이므로 점선 선택) 고차원 데이터셋에선 두 축에 직교하는 세 번째 축을 찾는다. 1,2,..n번째 축.

i번째 주성분이란 이러한 데이터에서 i번째 축을 말한다. 위의 그림에서 첫 PC는 벡터 c1의 축, 두번째 PC는 벡터 c2의 축.

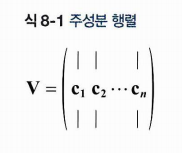
이러한 주성분을 어떻게 찾을까? 이때 특잇값 분해SVD 를 사용하고, 이는 표준 행렬을 분해해주는 기법이다. 훈련 세트 X를 세 개 행렬 곱셈인 $U\sum V^T$ 분해할 수 있다. V에는 찾고자 하는 주성분의 단위 벡터가 담겨 있다.

특잇값 분해를 알아보자

파이썬에서는 svd() 함수를 사용해 주성분을 구한 후, 처음 두 개의 PC를 정의할 수 있다.

X_centered = X - X.mean(axis=0)
U, s, Vt = np.linalg.svd(X_centered)
c1 = Vt.T[:, 0]
c2 = Vt.T[:, 1]

8.3.3 d차원으로 투영하기

이제 주성분을 추출했으니 처음 d개의 주성분으로 정의한 초평면에 투영하여 d로 차원을 축소하는 것이다.

이렇게 차원이 축소된 데이터셋 $X^d$ 를 얻기위해서는 행렬X와 V의 첫 d열로 구성된 행렬 $W_d$ 를 곱셈하면 된다.

W2 = Vt.T[:, :2]
X2D = X_centered.dot(W2)

8.3.4 사이킷런 사용

사이킷런에는 사실 아예 PCA 가 구현된 모델이 있다. 차원을 2로 줄이는 코드를 보자.

from sklearn.decomposition import PCA

pca = PCA(n_components=2)
X2D = pca.fit_transform(X)

이제 pca.components_.[:, 0] 을 찍으면 첫 주성분을 정의하는 단위 벡터를 확인할 수 있다.

8.3.5 설명된 분산의 비율

pca.explained_variance_ratio 로 주성분의 설명된 분산의 비율을 알 수 있다. 이는 각 주성분을 축을 따라 있는 데이터셋 분산 비율을 나타낸다. (분산 비율을 보존하는 것이 문제였다.)

pca.explained_variance_ratio_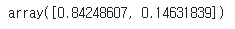

분산의 84%가 첫PC 를 따라, 14%가 두번째 PC를 따라 놓여있다는 것!

8.3.6 적절한 차원 수 선택?

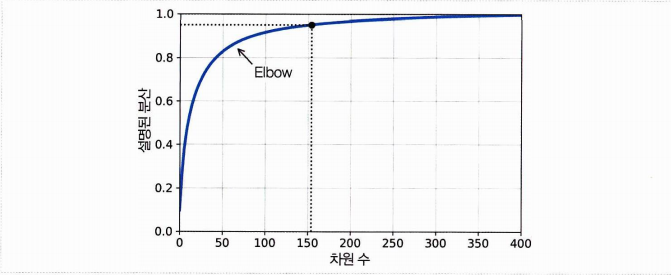
적절한 차원수는 임의로 정하기보다 충분한 분산이 될 때까지 더하면서 차원을 선택하는 것이 좋다.

다음 코드는 차원을 축소하지 않고 PCA를 계산, 95% 로 분산을 유지하는데 필요한 최소한의 차원 수를 계산한다.

pca = PCA()
pca.fit(X_train)
cumsum = np.cumsum(pca.explained_variance_ratio_)
d = np.argmax(cumsum >= 0.95) + 1

이제 d에는 95% 분산이 넘어가는 차원의 수가 담겨있다. 이제는 fit_transform 해주자! n_components = d 로 설정하면 된다.

그러나 그냥 처음부터 n_components 에 0.0부터 1.0 사이의 값을 주면 차원이 아닌 유지하고자 하는 분산 비율로 인식하여 자동으로 차원을 맞춘다.

pca = PCA(n_components=0.95)
X_reduced = pca.fit_transform(X_train)

추가로 cumsum 을 그래프 그리고 직접 시각화하여 결정하는 방법도 있다!

8.3.7 압축을 위한 PCA

• 차원을 축소하면 훈련 세트의 크기가 줄어든다

• MNIST 데이터셋에 적용하면 원래의 784개 특성이 아니라 150개 정도를 갖고 있도록 조정된다.

• 이런 크기 축소는 속도 향상에 기여.

• 다시 784개의 차원으로 되돌릴 수도 있다.

• 그러나 한 번 축소 후 복원의 경우 잃어버린 분산을 되돌릴 순 없다

• 원본 데이터와 재구성 데이터의 평균 제곱 거리를 재구성 오차라한다.

재구성 할 때에는 inverse_transform(축소데이터) 를 이용하자.

pca = PCA(n_components=154)
X_reduced = pca.fit_transform(X_train)
X_recovered = pca.inverse_transform(X_reduced)

또한 역변환 공식은 다음과 같다.

8.3.8 랜덤 PCA

PCA 를 선언할 때 svd_solver = 'randomized' 매개변수를 주면 랜덤 PCA라는 확률적 알고리즘을 사용해 d개의 주성분에 대한 근사값을 찾는다. 이때의 계산복잡도는 O(m X d^2) + O(d^3)

rnd_pca = PCA(n_components=154, svd_solver="randomized", random_state=42)
X_reduced = rnd_pca.fit_transform(X_train)

8.3.9 점진적 PCA

기존 PCA의 문제는 전체 훈련 세트가 메모리에 들어가야 한다는 것 > 점진적 PCA(IPCA) 개발, 미니배치로 나눈 뒤 하나씩 주입.

from sklearn.decomposition import IncrementalPCA

n_batches = 100
inc_pca = IncrementalPCA(n_components=154)
for X_batch in np.array_split(X_train, n_batches):
    inc_pca.partial_fit(X_batch)

X_reduced = inc_pca.transform(X_train)

이때는 반복문을 돌면서 배치 단위로 쪼갠 것을 fit(), 나중에 최종으로 transform 해주면 된다.