[핸즈온 머신러닝] 8. 차원 축소 (2)

차원 축소의 두 번째 내용을 정리해보자🤔

8.4 커널 PCA

커널 PCA란 차원 축소를 위해 비선형 투영을 수행하는 것이다.

일반적으로 커널 트릭이란 샘플을 고차원 공간(특성공간)으로 암묵적으로 매핑하는 것을 말하고, 고차원 공간에서 선형인 경계가 원본에서 복잡한 비선형이라는 것을 배웠다.

from sklearn.decomposition import KernelPCA

rbf_pca = KernelPCA(n_components=2, kernel="rbf", gamma=0.04)
X_reduced = rbf_pca.fit_transform(X)

KernelPCA를 선언하고, rbf 커널을 사용하는 코드이다.

다음 그림은 각각 선형 커널, rbf 커널, 시그모이드 커널을 사용하여 축소시킨 스위스 롤의 모습이다.

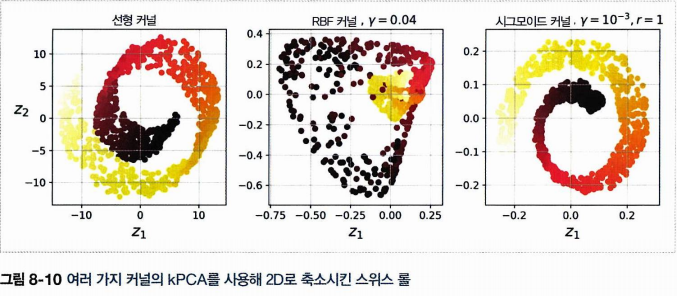
8.4.1 커널 선택과 하이퍼파라미터 튜닝

그렇다면 좋은 커널, 하이퍼파라미터는 어떻게 정할 것인가? 차원 축소는 (본래 비지도 학습)이나 종종 분류와 같은 문제의 전처리로 활용되므로 그리드 탐색을 사용할 수 있다.

from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline

clf = Pipeline([
        ("kpca", KernelPCA(n_components=2)),
        ("log_reg", LogisticRegression(solver="lbfgs"))
    ])

param_grid = [{
        "kpca__gamma": np.linspace(0.03, 0.05, 10),
        "kpca__kernel": ["rbf", "sigmoid"]
    }]

grid_search = GridSearchCV(clf, param_grid, cv=3)
grid_search.fit(X, y)

print(grid_search.best_params_)

• 기본 파이프라인은 KernelPCA 후 로지스틱회귀(분류) 진행.
• 탐색해야 할 것은 KernelPCA의 파라미터
• 현재 커널 후보는 rbf 와 시그모이드이다
• 감마의 후보는 0.03, 0.05, 10 이다
• 선언시 파이프라인과 그리드 탐색을 넣는다
• cv = 3 번
• bestparams 출력
  

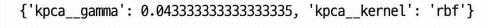
결과적으로 이러한 커널 트릭은 특성맵을 사용하여 훈련 세트를 무한차원의 특성공간에 매핑한 다음, 선형 PCA를 사용해 2D로 투영한 것과 동일하다.

재구성 원상이란 축소된 공간에서 다시 원본 공간의 포인트를 찾으려고 하는 것이다. (X > Y 의 함수일 때 Y 공역의 원소에 대응하는 X 정의역 원소로 이루어진 부분집합.)

pca.inverse_transform() 를 True 로 두고 사용하면 된다.

rbf_pca = KernelPCA(n_components=2, kernel="rbf", gamma=0.0433,
                    fit_inverse_transform=True)
X_reduced = rbf_pca.fit_transform(X)
X_preimage = rbf_pca.inverse_transform(X_reduced)

역시나 오차 계산은 MSE 사용.

from sklearn.metrics import mean_squared_error

mean_squared_error(X, X_preimage)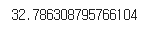

8.5 LLE

비선형 차원 축소의 또다른 방법으로 지역 선형 임베딩locally linear embedding(LLE) 가 있다. (투영에 의존하지 않는 매니폴드 학습이다.)

• 먼저 각 샘플이 가장 가까운 이웃에 얼마나 선형적으로 연관되어 있는지 측정한다
• 국부적인 관계가 가장 잘 보존되는 훈련세트의 저차원 표현을 찾는다
• 꼬인 매니폴드를 펼친다

from sklearn.manifold import LocallyLinearEmbedding

lle = LocallyLinearEmbedding(n_components=2, n_neighbors=10, random_state=42)
X_reduced = lle.fit_transform(X)

이쁘게 펼쳐진 것을 확인할 수 있다. 그러나 샘플 간 거리가 유지되어 있지는 않아보인다. 다시 LLE 작동 방식을 보자.

• 알고리즘이 각 샘플 x에 대해 가장 가까운 k개의 샘플을 찾는다. (closet neighbors)
• x와 $\sum wx$ 사이의 제곱 거리가 최소가 되는 w를 찾는다
• 이는 각 샘플에 대해 이웃과의 거리로 선형 함수를 재구성 하는 것이고, 이웃 과의 거리를 최소화 하는 w를 찾는 것이 목표이다

• 따라서 w_i,j에는 i번째 x와 j번째 x의 거리를 반영하는 가중치가 담겨있다.
• 이때 근접 이웃 k에 속하지 않을 때는 w = 0 이고 (조건 1)
• w를 모두 합하면 1이 되도록 하자 (조건 2)

이 단계를 거치면 가중치 행렬 W는 훈련 샘플 사이에 지역 선형 관계를 담는다. (쉽게 근접한 이웃 간의 거리를 표현한다고 보자.) 이제 해야할 것은 이 거리 관계를 유지하면서 차원을 축소하는 것이다.

이때 z^i는 차원이 축소된 x^i 이며, 가능한 (가중치 X z^j) 사이의 거리가 최소화되어야 한다. 따라서 이제 이를 최소화하는 Z를 찾으면 된다.

정리하면,
단계 1에서 W를 찾는 것은 샘플은 고정하고 거리가 최소가 되는 가중치를 찾는 것이다.
단계 2에서 Z를 찾는 것은 찾아낸 가중치를 고정하고 실제로 차원을 낮출 때 역시나 거리가 최소가 되도록 유지하는 것이다.

8.6 다른 차원 축소 기법

랜덤 투영, 다차원 스케일링, Isomap, t-SNE, LDA 등이 있다.