이상치는 왜 생길까

1. 아주 인간적인 실수에서 비롯
2. 데이터 자체가 손상되었을 수 있음
3. 실제로 뭔가 예외적인 일이 일어났기 때문. 예를들어 보통은 조용한 마을에 축제가 열려서 갑자기 소음이 많아진 경우

이상치의 유형

1. 단변량 이상치
   단 하나의 특징만 봐서 찾음
   예를 들어 사람들 키만 놓고 봤을때 평균적인 키에서 너무 멀리 떨어져 있는 경우를 말한다. 150~190cm사이의 사람들 사이에서 250cm의 거인이 나타난다면 그 사람의 데이터는 단변량 이상치

2. 다변량 이상치
   여러 특징을 함께 봐서 찾음
   예를 들어 사람의 키와 몸무게를 같이 고려한다
   예를들어 180cm에 50kg 인 사람이나 160cm에 100kg인 사람이 이에 해당

이상치가 데이터 집합에 미치는 영향

1. 예측의 오차가 커짐
2. 데이터의 일반적인 리듬이 깨짐
3. 결과가 한쪽으로 치우친다
4. 분석의 기본 규칙들이 흔들린다

이상치를 발견하는 방법

• 단변량 이상치 탐지

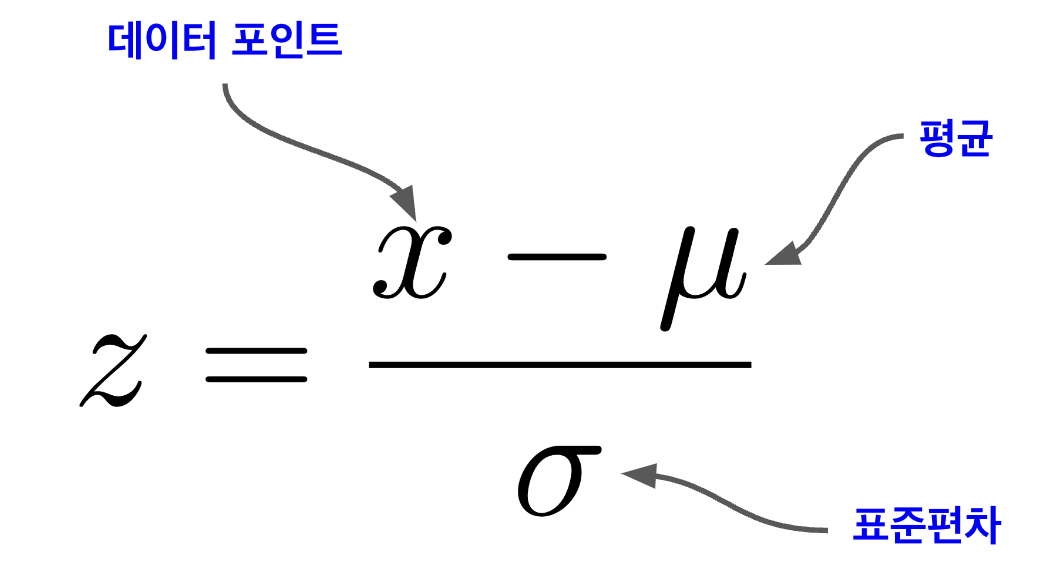
1. Z-Score(z-점수) :Z-Score는 데이터에서 표준편차를 활용해 이상치를 감지하는 간단하면서도 강력한 방법이다. 이 방법은 데이터를 표준화하고, 각 데이터 포인트가 평균으로부터 얼마나 떨어져 있는지를 계산하여 이상치를 식별한다. 특히 표준화된 데이터 세트에 효과적

2. IQR(Interquartile Range, 사분범위) : IQR은 데이터의 중앙값을 기준으로 하여 정상범위를 벗어나는 데이터 포인트를 찾아낸다. Q1과 Q3를 계산하고, 이를 기반으로 IQR을 구한 후, IQR을 이용하여 이상치를 탐지

• 다변량 이상치 탐지

3. DBSCAN (Density-Based Spatial Clustering of Applications with Noise) DBSCAN은 데이터 포인트들을 그룹화해서 이상치를 식별하는데 사용되는 클러스터링 알고리즘입니다. 데이터 포인트의 밀도를 기반으로 하며, 주변 데이터 포인트와의 관계를 고려하여 이상치를 찾아냅니다. 이 방법은 다양한 데이터 구조에서 유용합니다.

4. LOF (Local Outlier Factor) LOF는 데이터 포인트의 '지역적 밀도'를 측정하고, 이를 주변 포인트의 밀도와 비교하여 이상치를 탐지합니다. 주변 데이터 포인트와의 밀도 비율을 계산함으로써 이상치를 식별하며, 이 방법은 데이터의 지역적 밀도가 다를 때 효과적입니다.

이상치 탐지는 데이터 분석의 핵심 부분이며, 위에서 설명한 기법들은 다양한 데이터셋과 상황에 적용할 수 있습니다. 이러한 방법들을 이용하여 데이터에 숨어 있는 이상치를 효과적으로 식별할 수 있습니다.

Z-Score를 활용하여 이상치 발견

Z-score는 데이터 포인트가 데이터 세트의 평균으로부터 얼마나 떨어져 있는지 측정. 이를 통해 데이터 포인트가 전체 데이터 분포에서 어떤 위치에 있는지 파악할 수 있다.
이 방법은 데이터 세트 내에서 각 데이터 포인트의 상대적인 위치를 수치화하여, 데이터 포인트가 평균적인 범위 내에 있는지, 아니면 평균에서 벗아나 이상한 값을 가지는지를 판단하는데 사용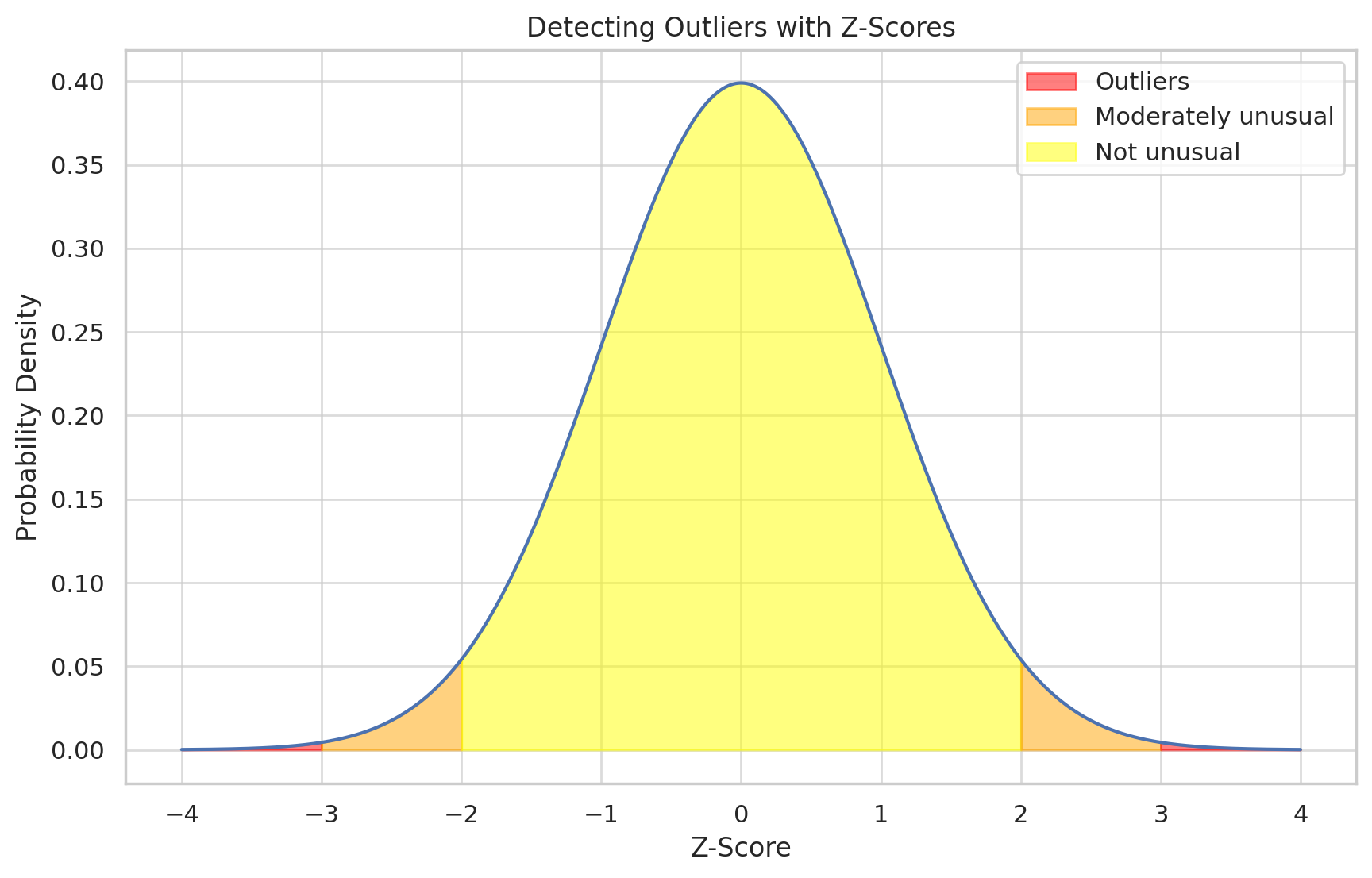

• Z-Score = 0: 데이터 포인트가 평균값에 정확히 일치합니다.
• Z-Score > 0: 데이터 포인트가 평균값보다 높습니다.
• Z-Score < 0: 데이터 포인트가 평균값보다 낮습니다.

z-score를 이용한 이상치 탐지 실습

1. z-socre 직접 계산 후 이상치 제거 : 이 방법에서는 데이터 세트의 평균과 표준편차를 사용하여 각 데이터 포인트의 z-socre를 수동으로 계산. 이후 설정한 z-score임계값을 넘는 데이터 포인트를 이상치를 판단하고 제거할 수 있다.

Z_train = X_train.copy()

# Train 데이터의 평균, 표준편차 계산
mean_train = Z_train['income_total'].mean()
std_train = Z_train['income_total'].std()

# 임계값 설정
threshold = 3

# Train 데이터로 Z-점수 계산 및 이상치 제거
Z_train['z_score_income'] = (Z_train['income_total'] - mean_train) / std_train
train_no_outliers = Z_train[Z_train['z_score_income'].abs() <= threshold]

train_no_outliers = train_no_outliers.drop('z_score_income', axis=1)
train_no_outliers.shape

2. Scipy를 이용한 Z-socre계산과 이상치 제거 : scipy 라이브러리의 stats 모듈은 z-score계산을 자동화 하는 함수를 제공한다. 이 함수를 사용하면 복잡한 계산 과정 없이도 쉽게 z-score를 계산할 수 있으며, 마찬가지로 설정한 임계값을 넘는 데이터 포인트를 식별하고 제거할 수 있다.

from scipy import stats

Z_scipy_train = X_train.copy()

# Train 데이터에 대해 Z-score 계산
Z_scipy_train['z_score_income'] = stats.zscore(Z_scipy_train['income_total'])

# 임계값 설정
threshold = 3

# 임계값을 기반으로 Train 데이터에서 이상치 제거
train_no_outliers = Z_scipy_train[Z_scipy_train['z_score_income'].abs() <= threshold]

# 임시 Z-score 컬럼 제거
train_no_outliers = train_no_outliers.drop('z_score_income', axis=1)
train_no_outliers.shape

장점 👍

• 간단하고 직관적
  Z-Score는 평균과 표준편차를 이용한 간단한 계산으로 이루어져 있어, 구현하기 쉽고 결과 해석이 직관적입니다.

• 표준화된 점수
  데이터 포인트가 데이터셋의 평균으로부터 얼마나 떨어져 있는지를 표준화된 형태로 표현하여, 서로 다른 데이터셋이나 변수 간 비교가 용이합니다.

• 정규 분포 데이터에 적합
  데이터가 정규 분포를 따르는 경우, Z-Score는 이상치를 식별하는 데 매우 효과적입니다.

• 확장성
  다양한 임계값 설정이 가능하며, 데이터의 특성에 맞게 조정할 수 있어 융통성이 뛰어납니다.

단점 👎

• 정규 분포 의존성
  Z-Score 방법은 데이터가 정규 분포를 가정할 때 가장 잘 작동합니다. 데이터가 크게 비대칭적이거나 긴 꼬리를 가진 경우, 이상치 탐지에 오류가 발생할 수 있습니다.

• 극단값에 민감
  극단적인 값이 포함된 경우, 이들 값이 평균과 표준편차에 큰 영향을 미칠 수 있으며, 이는 Z-Score 계산에 영향을 미칩니다.

• 모든 이상치를 식별하지 못할 수 있음
  Z-Score는 간단한 통계적 접근 방식이기 때문에, 모든 유형의 이상치를 완벽히 식별하지 못할 수 있습니다. 특히, 데이터셋에 이상치가 많은 경우 효과적이지 않을 수 있습니다.

• 이진 결정의 어려움
  어떤 데이터 포인트를 이상치로 간주할지에 대한 명확한 기준이 없기 때문에, 임계값 설정이 주관적일 수 있으며, 이에 따라 결과가 달라질 수 있습니다.

Z-Score를 이용한 이상치 제거 방법은 이러한 장단점을 고려하여 신중히 적용해야 하며, 경우에 따라 다른 이상치 탐지 방법과 병행하여 사용하는 것이 좋습니다. 데이터의 특성과 분석 목적에 따라 적절한 방법을 선택하는 것이 중요합니다.

IQR을 활용하여 이상치 발견

IQR(Interquartile Range)은 데이터 세트의 중간 50% 범위를 측정하는 통계적 방법. 데이터의 중간값 주변의 변동성을 파악하는데 유용하다.
구체적으로, IQR은 데이터 세트의 제1사분위수와 제3사분위수 사이의 차이로 정의된다.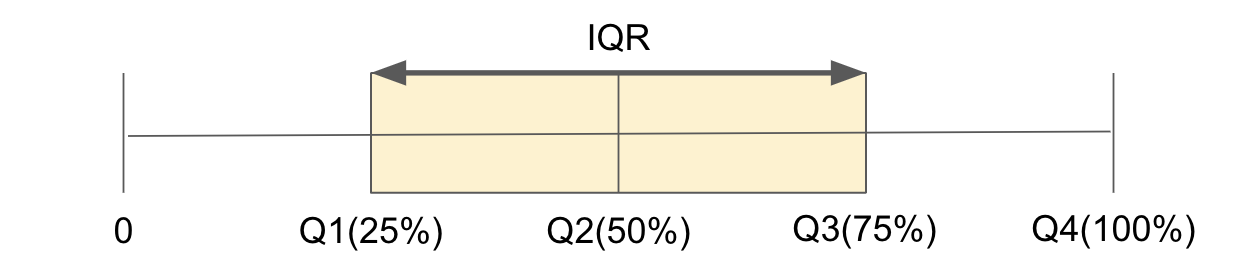

• IQR의 계산 방법
  IQR은 데이터셋의 1사분위수와 3사분위수를 계산함으로서 얻어진다
  Q1은 데이터셋의 하위25%에 해당하는 값이고, Q3는 상위 25%에 해당하는 값
  따라서 IQR은 Q3 - Q1로 계산되며, 이는 데이터의 중간 범위에 대한 전반적인 퍼짐 정도를 나타냄

quantile 함수를 활용하여 IQR 이상치 제거

lower_bound, upper_bound = out_iqr(X_train['income_total'])
train_no_outliers_iqr = X_train[(X_train['income_total'] >= lower_bound) & (X_train['income_total'] <= upper_bound)]

print("Shape of train data after removing outliers using IQR:", train_no_outliers_iqr.shape)

percentile() 함수를 활용하여 iqr 이상치 제거

Q1 = np.percentile(X_train['income_total'], 25)
Q3 = np.percentile(X_train['income_total'], 75)

IQR = Q3 - Q1
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR

train_no_outliers_iqr = X_train[(X_train['income_total'] >= lower_bound) & (X_train['income_total'] <= upper_bound)]
print("Shape of train data after removing outliers using NumPy's percentile:", train_no_outliers_iqr.shape)

IQR 를 활용한 이상치 탐지의 장점과 단점

장점 👍
극단치에 대한 강한 내성
IQR은 데이터 세트의 중앙 부분에 초점을 맞추므로 극단적인 값을 가진 이상치의 영향을 덜 받습니다. 이는 데이터가 비대칭적인 분포를 가질 때 특히 유용합니다.

직관적 이해
IQR은 사분위수라는 기본적인 통계 개념에 기반하여, 데이터의 중간 범위를 쉽게 이해하고 해석할 수 있게 합니다.

비모수적 접근
IQR 방법은 데이터가 특정 분포(예: 정규 분포)를 따르지 않는 경우에도 사용할 수 있습니다. 이는 데이터가 다양한 형태의 분포를 가질 수 있는 실제 상황에서 유용합니다.

단점 👎
정보 손실의 가능성
이상치로 간주되는 데이터 포인트를 제거하면 중요한 정보를 잃을 수 있습니다. 특히, 이상치가 데이터에 대한 중요한 신호를 포함하고 있을 경우, 이러한 정보 손실은 분석 결과에 부정적인 영향을 미칠 수 있습니다.

임의의 임계값 설정
이상치를 정의하는 데 사용되는 임계값(예: 1.5 x IQR)은 어느 정도 임의적입니다. 이 임계값은 상황에 따라 조정되어야 할 수 있으며, 이에 대한 명확한 가이드라인이 없는 경우가 많습니다.

IQR 방법은 데이터의 중간 범위를 분석하여 이상치를 탐지하는 효과적인 방법으로, 특히 극단값이 포함된 데이터 세트에 적합합니다. 그러나 이상치를 어떻게 처리할지는 데이터의 성격과 분석 목적에 따라 신중하게 결정해야 합니다.