DBSCAN(Density-based spatial clustering of applications with noise)을 활용하여 이상치 발견

DBSCAN 이란?

DBSCAN은 데이터 포인트들을 기반으로 클러스터를 형성하고, 이 과정에서 클러스터에 속하지 않는 포인트들을 이상치로 간주하는 클러스터링 알고리즘

k-means알고리즘의 대안으로 사용되며, 미리 클러스터의 수를 정할 필요 없이 데이터 자체의 밀도에 기반하여 클러스터링을 수행

1. 핵심포인트

• 핵심포인트는 '주변지역에 일정 수 이상의 이웃 포인트가 있는 데이터 포인트'이다
• 이 포인트들은 클러스터링 과정에서 클러스터의 핵심을 형성한다

2. 경계 포인트

• 경계 포인트는 '핵심 포인트의 이웃이지만, 그 자체로는 핵심 포인트의 조건을 충족하지 않는 포인트'
• 이들은 클러스터의 경계를 형성

3. 노이즈 포인트

• 핵심 포인트나 경계 포인트가 아닌 모든 포인트로 어떤 클러스터에도 속하지 않는다
• 이 포인트들은 데이터셋에서 이상치를 나타낸다

DBSCAN 알고리즘의 작동 원리

DBSCAN은 밀도 기반 공간 클러스터링이고, 데이터의 공간에서 각 데이터 포인트 주변에 epsilon반경의 원을 형성하고, 이를 기반으로 데이터 포인트를 핵심 포인트, 경계포인트, 노이즈 포인트로 분류한다.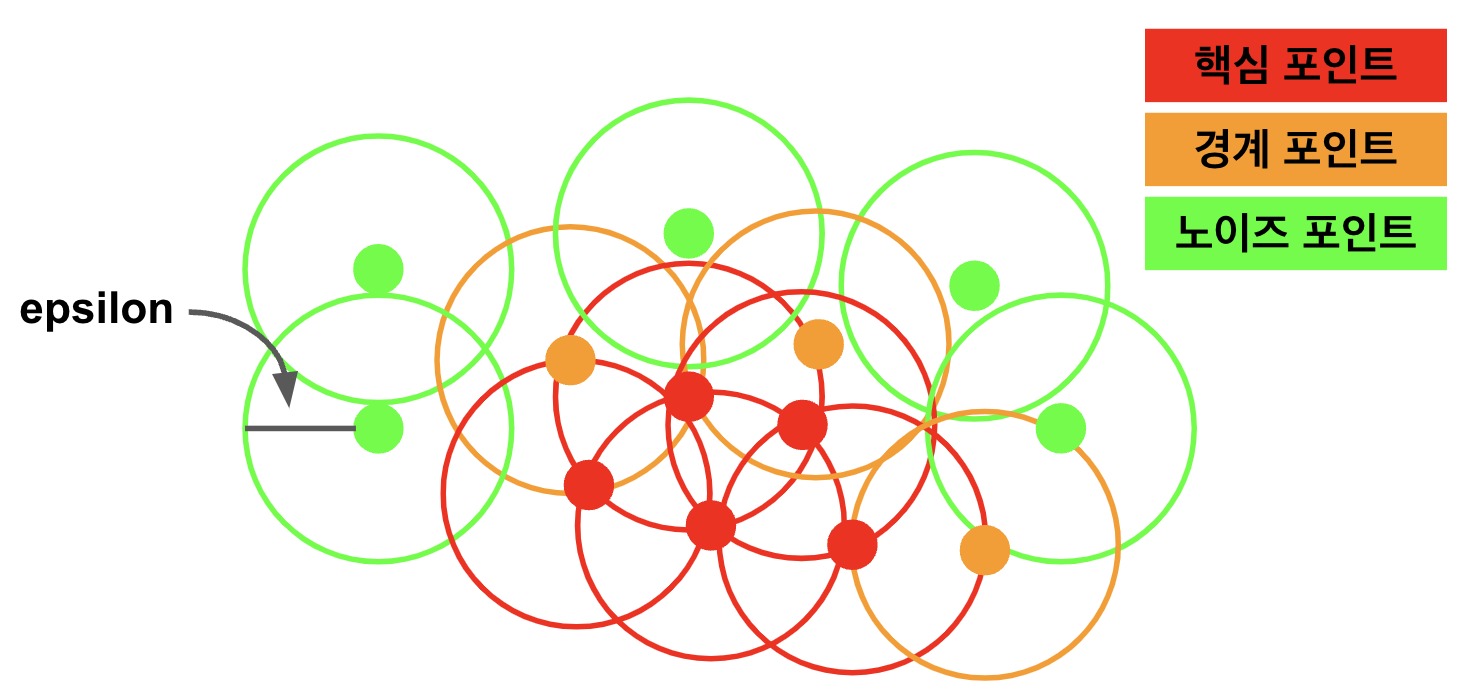
이 때 고려해야 하는 두 가지 주요 매개변수는 epsilon(엡실론) 과 minPoints(최소 데이터 포인트 수) 입니다.
epsilon은 각 데이터 포인트 주변에 형성되는 원의 반경으로, 데이터 포인트 간의 밀도를 정의하며,
minPoints는 해당 원 내부에 존재해야 하는 최소 데이터 포인트 수로, 해당 데이터 포인트를 핵심 포인트로 분류하기 위한 조건입니다.

DBSCAN을 이용한 이상치 탐지

'공복 혈당'과 '중성 지방'이라는 두 가지 수치형 변수를 사용하여 DBSCAN 클러스터링을 수행하는 과정을 확인

from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler

# 데이터 준비
DBSCAN_train = X_train.copy()

numeric_columns = ['공복 혈당', '중성 지방']
data_numeric = DBSCAN_train[numeric_columns]

# 데이터 표준화
scaler = StandardScaler()
data_scaled = scaler.fit_transform(data_numeric)

# DBSCAN 클러스터링 (eps와 min_samples는 상황에 따라 조정 필요)
db = DBSCAN(eps=0.5, min_samples=5).fit(data_scaled)  
labels = db.labels_

pd.Series(labels).value_counts()

• DBSCAN 클러스터링을 통한 이상치 제거

clusters_sample = db.fit_predict(data_scaled)

DBSCAN_train['clusters'] = clusters_sample
sample_no_outliers = DBSCAN_train[DBSCAN_train['clusters'] != -1]

display(sample_no_outliers.head(3))
display(f"이상치가 아닌 데이터 포인트들의 수: {len(sample_no_outliers)}")

DBSCAN을 활용한 이상치 탐지의 장단점

장점 👍

• 모델 가정 불필요
  DBSCAN은 클러스터의 형태에 대한 가정을 하지 않기 때문에, 원형이 아닌 클러스터를 잘 탐지할 수 있습니다.

• 클러스터 개수 설정 불필요
  클러스터의 개수를 사전에 정할 필요가 없습니다. DBSCAN은 데이터로부터 클러스터의 개수를 자동으로 결정합니다.

• 이상치에 강건함
  DBSCAN은 밀도가 낮은 영역의 데이터 포인트를 자연스럽게 이상치로 분류합니다.

• 노이즈와 클러스터 구분
  알고리즘이 이상치를 노이즈로 간주하여 데이터에서 자연스럽게 분리합니다.

• 데이터의 밀도에 따른 유연성
  eps와 min_samples 파라미터를 조정하여 다양한 밀도를 가진 데이터셋에 적용할 수 있습니다.

단점 👎

• 파라미터 설정
  eps와 min_samples 같은 파라미터 설정이 결과에 큰 영향을 미치며, 최적의 값을 찾기 위해 여러 시도가 필요할 수 있습니다.

• 변수 스케일의 민감성
  DBSCAN은 변수의 스케일에 민감하기 때문에, 스케일링과 같은 사전 데이터 처리가 중요합니다.

• 고차원 데이터의 어려움
  '차원의 저주'로 인해, 고차원 데이터에서 성능이 저하될 수 있습니다.

• 밀도 변화에 민감
  데이터셋 내에서 밀도가 크게 변할 경우, 한 가지 eps 값으로 모든 클러스터를 적절히 식별하기 어렵습니다.

• 클러스터 크기의 다양성
  매우 다양한 밀도를 가진 클러스터가 존재하는 경우, 모든 클러스터를 동일하게 잘 식별하지 못할 수 있습니다.

LOF(Local Outlier Factor)를 활용하여 이상치 발견하기

LOF란

주변 이웃과 비교하여 데이터 포인트가 얼마나 이상한지를 평가하는 알고리즘
이 방법은 각 데이터 포인트의 지역적 밀도를 계산하고, 이를 해당 포인트의 이웃들의 밀도와 비교
LOF 점수는 데이터 포인트가 얼마나 주변 이웃과 다른지를 나타내며, 이 점수가 높을수록 해당 포인트는 이상치일 가능성이 높다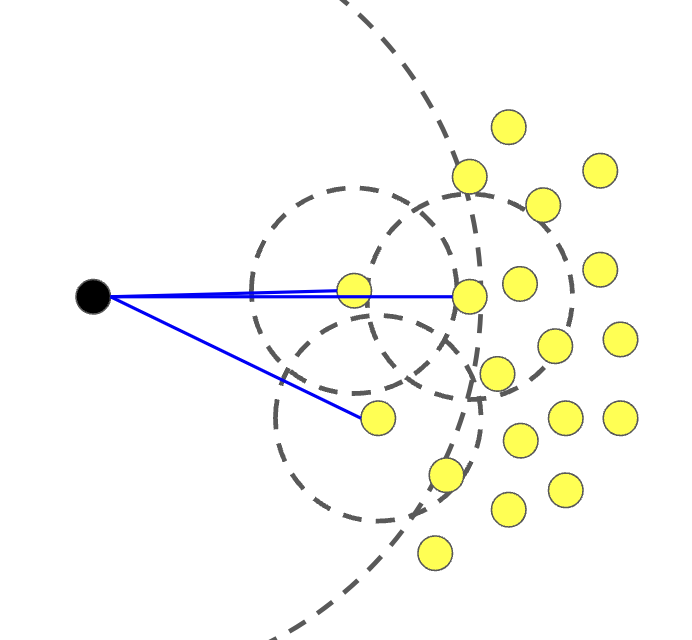

LOF 알고리즘의 작동 원리

• 이웃 개수 설정 : LOF알고리즘을 시작하기 전에, 고려할 각 데이터 포인트의 이웃 수를 결정해야한다. 이웃의 수는 알고리즘이 얼마나 지역적으로 데이터를 보는지 결정한다.
• 지역 밀도 계산 : 각 데이터 포인트의 지역 밀도를 계산한다. 이것은 n_neighbors개의 가장 가까운 이웃까지의 거리를 기반으로 하며, 이웃들 사이의 평균 거리로 표현할 수 있다.
• LOF 점수 계산 : 각 데이터 포인트의 LOF점수를 계산한다. 이 점수는 데이터 포인트의 지역 밀도를 그 이웃들의 밀도와 비교함으로서 결정. LOF점수가 1에 가까우면 데이터 포인트는 이웃보다 밀도가 낮은 영역에 위치해 있으며, 이는 이상치일 가능성이 높음을 의미한다.
• 이상치 결정 : LOF점수가 특정 임계값 이상인 데이터 포인트를 이상치로 분류한다. 이 임곗값은 일반적으로 경험적으로 경정되거나, 특정 비율의 데이터 포인트가 이상치로 분류되도록 설정할 수 있다.
• 이상치 제거 : 이상치로 판정된 데이터 포인트를 데이터 세트에서 제거

LOF를 활용한 이상치 탐지의 장단점

장점 👍

• 지역적 밀도 차이 기반
  LOF는 각 데이터 포인트의 지역적 밀도를 고려하여 이상치를 탐지합니다. 이 방법은 데이터셋의 전반적인 밀도 분포와 상관없이, 지역적 관점에서 이상치를 정확하게 식별할 수 있게 해줍니다.

• 다양한 데이터셋에 적용 가능
  LOF는 다양한 형태와 밀도를 가진 데이터셋에 적용될 수 있으며, 특히 밀도가 불균일한 데이터셋에서 유용합니다.

• 이상치의 순위화
  LOF는 단순히 이상치를 식별하는 것이 아니라, 이상치로 판단되는 정도를 점수로 제공합니다. 이를 통해 이상치들 사이에서도 상대적인 이상도를 평가할 수 있습니다.

• 파라미터 조정의 유연성
  사용자는 이웃의 수(n_neighbors)와 같은 파라미터를 조정하여 알고리즘의 민감도를 조절할 수 있습니다.

단점 👎

• 파라미터 선택의 어려움
  올바른 n_neighbors 값을 선택하는 것이 중요하며, 이 값에 따라 이상치 탐지 결과가 크게 달라질 수 있습니다. 적절한 값 설정은 종종 경험적인 접근이 필요합니다.

• 고차원 데이터에 대한 한계
  고차원 데이터에서 거리 기반 알고리즘은 "차원의 저주"의 영향을 받을 수 있으며, 이는 LOF의 성능 저하로 이어질 수 있습니다.

• 계산 복잡성
  특히 큰 데이터셋에서는 각 데이터 포인트의 이웃을 찾는 과정이 계산적으로 복잡할 수 있습니다.

• 데이터 스케일에 민감
  서로 다른 스케일의 변수를 포함한 데이터셋에서 LOF를 사용하기 전에 적절한 스케일링이 필요할 수 있습니다.